
Контрольные вопросы к лекции 3
Изобразите упрощенную схему цилиндрической зубчатой передачи и укажите величину межосевого расстояния.
На схеме укажите, какое зубчатое колесо является шестерней, а какое колесом.
Дайте определение модуля передачи.
Назовите кривую образующую рабочую поверхность зуба.
Что определяет коэффициент торцевого перекрытия?
Изобразите схему сил действующих в цилиндрической прямозубой передаче.
Какие нормы определяют степень точности передачи, определите их смысл.
Запишите связь окружной силы в передаче с величиной крутящего момента и размерами зубчатого колеса.
Лекция №4
Тема лекции: Критерии работоспособности зубчатых передач.
Потеря работоспособности зубчатых передач происходит из-за одной или совокупности следующих причин.

Усталостное выкрашивание: выпадение с рабочей поверхности зуба частиц металла. В результате уменьшается площадь рабочей поверхности зуба и возникают концентраторы напряжений около образовавшихся ямок, что приводит к ускорению процесса выкрашивания.
Излом зуба у основания от напряжений изгиба.
Пластические деформации поверхности зуба.
Поверхностный износ.
В ид
потери работоспособности зависит от
условий эксплуатации передачи. Передачи
могут быть открытыми-1 и закрытыми-2.
ид
потери работоспособности зависит от
условий эксплуатации передачи. Передачи
могут быть открытыми-1 и закрытыми-2.
Открытые передачи не имеют корпуса и надежной смазки и поэтому не защищены от воздействия пыли, грязи и влаги. Поэтому, для них причинами потери работоспособности являются износ от трения поверхностей зубьев, пластические деформации и поломка зуба от ударов и перегрузок.
Закрытые передачи имеют закрытый корпус и масляную ванну, в которую погружаются зубья колес и при их вращении смазка попадает в зону зацепления, исключая контакт поверхностей зубьев по металлу, заменяя его контактом через масляную пленку. Это резко уменьшает износ зуба, повышая срок службы и, поэтому потеря работоспособности происходит из-за усталостного выкрашивания поверхности, пластических деформаций и поломки зуба при перегрузках.
Большая часть зубчатых передач выполняется в закрытом варианте, и потеря работоспособности происходит по механизму усталостного выкрашивания. Причиной этого является следующий процесс. Рабочая поверхность зуба подвергается нагружению и деформации при контакте с зубом сопряженного зубчатого колеса. Этот процесс имеет циклический характер.
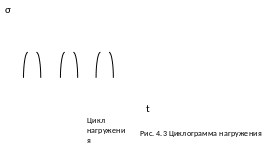


Силы Fn, действующие в зоне контакта зубьев вызывают местную деформацию с образованием площадки контакта-А. На этой площадке возникают контактные напряжения -σH, максимальная величина которых является мерой напряженного состояния зуба и служит причиной накопления усталостных явлений и выкрашивания поверхностных слоев. Контактные напряжения возникают в деталях, у которых при работе площадь поверхности соприкосновения с другой деталью несоизмеримо мала по сравнению с размерами самой поверхности детали. Максимальная величина возникающих при этом напряжений может быть рассчитана с помощью теории контактных напряжений Герца (Herz). Она позволяет связать величину этих напряжений с размерами и формой поверхности тел и приложенными усилиями. Формула Герца имеет вид.
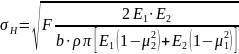 .
(4.1)
.
(4.1)
Здесь
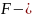 нормальная к поверхности контакта сила;
нормальная к поверхности контакта сила;
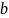 -
длина линии контакта (для зубчатых колес
это ширина колеса);
-
длина линии контакта (для зубчатых колес
это ширина колеса);
 -
приведенный радиус кривизны контактирующих
поверхностей;
-
приведенный радиус кривизны контактирующих
поверхностей;
 .
(4.2)
.
(4.2)
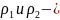 радиусы кривизны
двух поверхностей;
радиусы кривизны
двух поверхностей;
З нак
+ относится к случаю внешнего контакта
-
нак
+ относится к случаю внешнего контакта
-
Знак – относится к случаю внутреннего контакта -

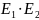 - модули упругости
материалов контактирующих тел;
- модули упругости
материалов контактирующих тел;
μ1 и μ2 – коэффициенты Пуассона материалов зубчатых колес.
Для обеспечения работоспособности зубчатых передач величина действующих контактных напряжения не должна превышать определенной их величины. Для определения этой величины проводятся испытания материалов при различных значениях рабочих контактных напряжений, и фиксируется время начала усталостного выкрашивания. В результате получаем зависимость следующего вида.

I
σH1
Рис. 4.5 Кривая выносливости
 NH1
NH1
Это зависимость контактной выносливости. Над кривой находится зона разрушения – здесь происходит потеря работоспособности. Под кривой- рабочая зона. На горизонтальной оси – N фиксируется число циклов нагружения до момента начала интенсивного усталостного выкрашивания. На графике видно, что при напряжении равном и меньшем величины σHO усталостное выкрашивание не происходит и срок службы детали при контактном нагружении стремится к бесконечности. Это напряжение является одной их механических характеристик материала и называется пределом контактной выносливости. И для этого случая нагружения выделяется зона III называемая зоной неограниченной выносливости. Ей соответствует число циклов нагружения NHO называемое базовым числом циклов нагружения. Если величина контактных напряжений велика, то потеря работоспособности передачи происходит из-за развития пластической деформации рабочей поверхности зубьев. Работа в таких условиях ограничивается малым числом циклов нагружения N МЦ т.е. малым сроком службы и называется малоцикловым разрушением. Работа в таком режиме нагружения на кривой контактной выносливости соответствует первой зоне.
Наиболее интересной является вторая зона – зона ограниченной выносливости. При работе в ней имеет место зависимость между действующей величиной контактных напряжений и предельным числом циклов нагружения (т.е. сроком службы) до момента начала заметного усталостного выкрашивания. При работе с контактными напряжениями σH1 можем прогнозировать срок службы (число циклов нагружения) - NH1. Наоборот, если известен требуемый ресурс - срок службы передачи, то можно рассчитать число циклов нагружения за этот срок и определить величину допустимых контактных напряжений и использовать её в проектном расчете передачи.
Однако, на практике определение расчетных контактных напряжений требует учета целого ряда дополнительных факторов. Во первых, для определения этого напряжения удобно использовать одну из характеристик материала зубчатого колеса, а именно предел контактной выносливости - σHO. Учет требуемого числа циклов нагружения Ni производится с помощью коэффициента долговечности KHL.
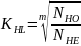 ,
(4.3)
,
(4.3)
Здесь: m – показатель кривизны кривой контактной выносливости на участке второй зоны, при расчете на выносливость он равен 6;
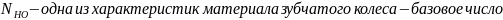

Эта величина определяется в зависимости от твердости поверхностного слоя материала.
 .
.
HB – средняя твердость материала по шкале твердости Бринелля. Средняя твердость используется потому, что термообработка - процесс не позволяющий получить точное значение твердости, а дающий некоторый вероятностный интервал, например 270…295 HB. Среднее значение этого интервала и используется в расчете.
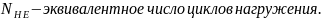 Эта величина
учитывает фактическое число циклов
нагружения и режим нагружения.
Эта величина
учитывает фактическое число циклов
нагружения и режим нагружения.
 .
(4.4)
.
(4.4)
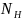 -
фактическое число циклов нагружения.
-
фактическое число циклов нагружения.
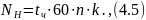
 -
ресурс работы зубчатого колеса в часах;
-
ресурс работы зубчатого колеса в часах;
 -
частота
вращения зубчатого колеса в оборотах
в минуту;
-
частота
вращения зубчатого колеса в оборотах
в минуту;
 -
коэффициент, учитывающий кратность
зацепления (т.е. со сколькими зубчатыми
колесами зацепляется данное зубчатое
колесо).
-
коэффициент, учитывающий кратность
зацепления (т.е. со сколькими зубчатыми
колесами зацепляется данное зубчатое
колесо).


Рис. 4.6
k=1 k=2
Левая схема: оба зубчатых колеса зацепляются с одним зубчатым колесом - кратность зацепления для каждого из этих колес равна 1. Правая схема: центральное зубчатое колесо зацепляется с двумя зубчатыми колесами, за один оборот каждый его зуб вступает в контакт с зубьями малых зубчатых колес (шестерен) два раза, кратность зацепления для него равна 2. У малых зубчатых колес (шестерен) каждый их зуб за один оборот шестерни вступает в контакт с зубьями большего по диаметру зубчатого колеса (колесом) один раз. Поэтому для каждой шестерни правой схемы кратность зацепления равна 1.
Выражение
4.4 содержит коэффициент
 .
Этот коэффициент учитывает режим
нагружения, в котором работает
рассчитываемое зубчатое колесо.
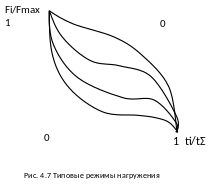
Существует 6 типовых режимов нагружения.
.
Этот коэффициент учитывает режим
нагружения, в котором работает
рассчитываемое зубчатое колесо.
Существует 6 типовых режимов нагружения.
1
2
3
4
5
При работе конструкции нагрузка обычно изменяется во времени и при проектировании обычно оговаривается наиболее вероятный режим нагружения.
0 – постоянный режим;
1 - тяжелый режим;
2- средний равновероятностный;
3 – средний нормальный;
4 – легкий;
5
Fi/Fmax 1
ti/t Σ
Учет
влияния на выносливость фактического
режима нагружения и производится с
помощью коэффициента
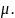
Этот коэффициент может принимать следующие значения.
Таблица 4.1
-
№ режима
0
1
2
3
4
5
1
0,5
0,25
0,18
0,125
0,063
Определяемый
выражением 4.3 коэффициент режима
нагружения
 для материалов с однородной структурой
может принимать значение в интервале
от 1 (при равенстве расчетного и базового
чисел циклов нагружения) до 2,6 на границе
I зоны, где начинает
работать другой механизм потери
работоспособности. Для материалов с
поверхностной термообработкой (ХТО,
закалка ТВЧ) верхняя граница – 1,8.
для материалов с однородной структурой
может принимать значение в интервале
от 1 (при равенстве расчетного и базового
чисел циклов нагружения) до 2,6 на границе
I зоны, где начинает
работать другой механизм потери
работоспособности. Для материалов с
поверхностной термообработкой (ХТО,
закалка ТВЧ) верхняя граница – 1,8.
Здесь следует отметить, что зона III на кривой контактной выносливости, строго говоря, не гарантирует полного отсутствия развития усталостных процессов при работе в ней. Поэтому для полной гарантии выработки деталью требуемого ресурса, при расчете допускаемого контактного напряжения необходимо учитывать коэффициент долговечности, определяемый зависимостью 4.3, но значение коэффициента m для третьей зоны следует принимать равным 20.
Закладываемая в расчет величина σHO – предел контактной выносливости не является константой, а определяется с учетом твердости поверхностного слоя материала.
Таблица 4.2
-
Термообработка
Твердость
поверхности
Материал
σHO
Нормализация или улучшение
< 350 HB
Сталь углеродистая и легированная
2 HBср +70
Закалка
поверхностная или обьемная
40…56 HRC
17 HRCср + 200
Цементация
56 HRC
Сталь легированная
23 HRCср
азотирование
>52 HRC
1050
Таким образом, закладываемое в проектный расчет контактное напряжение будет определяться зависимостью:
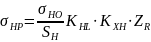 .
(4.6)
.
(4.6)
Здесь
появляется коэффициент
 - коэффициент запаса, который
принимается равным 1,1 для материалов с
однородной объемной термообработкой
и равным 1,2 с поверхностной термообработкой.
Коэффициент
- коэффициент запаса, который
принимается равным 1,1 для материалов с
однородной объемной термообработкой
и равным 1,2 с поверхностной термообработкой.
Коэффициент
 учитывает возможную реверсивность
нагрузки, а коэффициент
учитывает возможную реверсивность
нагрузки, а коэффициент
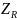 учитывает шероховатость поверхности
зуба.
учитывает шероховатость поверхности
зуба.
Контрольные вопросы к лекции 4
Перечислите виды разрушения зубчатых колес.
В чем различие между открытой и закрытой зубчатыми передачами?
Какую роль играет смазка при работе зубчатой передачи?
В каких случаях возникают контактные напряжения?
Какие механические характеристики материалов зубчатых колес определяют величину действующих контактных напряжений?
Что такое σHO?
Что определяет коэффициент
 ?
?Что учитывает коэффициент кратности зацепления?
Чем отличаются различные режимы нагружения?
Почему коэффициент долговечности не может быть большим 2,6?
Лекция №5
Тема лекции: Расчет цилиндрических зубчатых передач на контактную выносливость.
Смысл расчета заключается в определении действующих в передаче контактных напряжений и сравнении их с допускаемыми напряжениями. Расчет основан на формуле Герца (4.1).
.
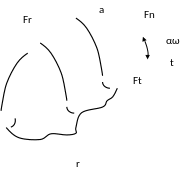 Для
определения действующих в передаче
напряжений эту зависимость следует
преобразовать применительно к параметрам
цилиндрической зубчатой передачи.
Начнем с
Для
определения действующих в передаче
напряжений эту зависимость следует
преобразовать применительно к параметрам
цилиндрической зубчатой передачи.
Начнем с
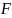 – нормальной, т. е. перпендикулярной
к поверхности контакта зубьев силы.
– нормальной, т. е. перпендикулярной
к поверхности контакта зубьев силы.

Анализ проведем для прямозубой передачи. Сила для удобства анализа раскладывается на две проекции. В направлении оси t касательной к начальной окружности колеса и перпендикулярной к его оси – проекция Ft – окружная (или тангенциальная)сила. Она связана с нормальной силой через угол зацепления αω. Вторая проекция Fr – радиальная сила.
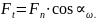 (5.1)
(5.1)
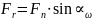 .
.
Для
нахождения нормальной силы
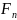 воспользуемся
первым выражением из (5.1) и соотношением:
воспользуемся
первым выражением из (5.1) и соотношением:

Тогда сможем найти выражение для .
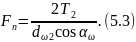
В этом выражении присутствует крутящий момент на колесе, который либо задается при проектировании передачи, либо определяется по заданным при проектировании величине передаваемой мощности Р и частоте вращения колеса n.
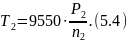
Угол
зацепления
для эвольвентных передач равен 200.
Неизвестным является только диаметр
начальной окружности
 .
Он будет выражен через межосевое
расстояние передачи и её передаточное
число. Вторая величина, которую следует
выразить через параметры зубчатой
передачи – b
.
Он будет выражен через межосевое
расстояние передачи и её передаточное
число. Вторая величина, которую следует
выразить через параметры зубчатой
передачи – b - длина контактирующих поверхностей
- длина контактирующих поверхностей Для прямозубой передачи это ширина
зубчатого венца (ширина колеса) - b
Для прямозубой передачи это ширина
зубчатого венца (ширина колеса) - b
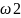 .
Она может быть выражена через
межосевое расстояние передачи αω
с помощью коэффициента ширины
зубчатого колеса Ψbα.
Этот коэффициент задается при
проектировании передачи из стандартного
ряда.
.
Она может быть выражена через
межосевое расстояние передачи αω
с помощью коэффициента ширины
зубчатого колеса Ψbα.
Этот коэффициент задается при
проектировании передачи из стандартного
ряда.
.
Ψbα= b / αω. (5.5)
Последняя
неизвестная величина
- приведенный радиус кривизны поверхности
контактирующих зубьев. Радиус кривизны
зуба шестерни в момент нахождения точки
зацепления в полюсе может быть определен
из треугольника О1А 1П
(рис.3.1). В нем О1П – радиус начальной
окружности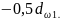 αω
–известный
угол зацепления. О1А1- радиус
кривизны эвольвенты и следовательно
зуба шестерни в момент нахождения точки
контакта в полюсе П. Поэтому можем
выразить радиус кривизны шестерни как:
αω
–известный
угол зацепления. О1А1- радиус
кривизны эвольвенты и следовательно
зуба шестерни в момент нахождения точки
контакта в полюсе П. Поэтому можем
выразить радиус кривизны шестерни как:
 (5.6)
(5.6)
Аналогичным образом определяется радиус кривизны для зуба колеса.
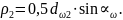 (5.7)
(5.7)
Таким образом, приведены радиус кривизны найдем из выражения:
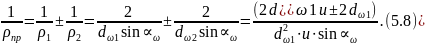
или
 .
(5.9)
.
(5.9)
Здесь использовано условие, что
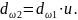 (5.10)
(5.10)
Ширина зубчатого колеса может быть выражена из (5.5).
Из (5.3) найдем

Если принять, что зубчатые колеса выполнены из стали, то модуль упругости E равен 2,1.1011 Па, а коэффициент Пуассона μ равен 0,3. С учетом этих условий выражение (4.1) примет вид.

Выразим
в этом выражении
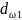 и
через
межосевое расстояние
и
через
межосевое расстояние
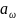 .
.

 (5.13)
(5.13)
Заменим в выражении (5.12) величины и через их значение из (5.13).
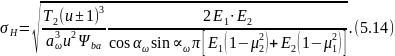
Если
в этой зависимости заложить условие,
что оба зубчатых колеса выполнены из
стали, для которой модуль упругости
 равен
2,1
равен
2,1 1011
Па, а коэффициент Пуассона μ равен
0,3. Наложить условие, что передача
является эвольвентной, для которой
угол профиля инструментальной рейки
равен 200, то после разрешения этого
неравенства относительно
1011
Па, а коэффициент Пуассона μ равен
0,3. Наложить условие, что передача
является эвольвентной, для которой
угол профиля инструментальной рейки
равен 200, то после разрешения этого
неравенства относительно
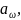 получим
зависимость для проектного расчета
прямозубых цилиндрических передач.
получим
зависимость для проектного расчета
прямозубых цилиндрических передач.

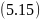
В
этой зависимости коэффициент
 включает
числовое значение модуля упругости,
коэффициента Пуассона, величину угла
профиля рейки для эвольвентных передач,
а также условие, что крутящий момент
подставляется в Нм, а допускаемое
контактное напряжение σHP
в МПа. Также учтено, что результат
получаем в метрах и переводим его в
миллиметры. С учетом этих условий
значение коэффициента для прямозубых
передач составит 490 МПа1/3.
включает
числовое значение модуля упругости,
коэффициента Пуассона, величину угла
профиля рейки для эвольвентных передач,
а также условие, что крутящий момент
подставляется в Нм, а допускаемое
контактное напряжение σHP
в МПа. Также учтено, что результат
получаем в метрах и переводим его в
миллиметры. С учетом этих условий
значение коэффициента для прямозубых
передач составит 490 МПа1/3.
В
данную зависимость введен коэффициент
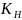 учитывающий динамичность режима
нагружения.
учитывающий динамичность режима
нагружения.
Зависимость получена для прямозубых эвольвентных передач. Эвольвента – кривая, описывающая траекторию конца нитки сматываемой с неподвижной катушки. Кроме эвольвентных зубчатых передач существуют передачи с круговым профилем зуба (профиль – дуга окружности), а также передачи с циклоидальным профилем зуба. Циклоида – траектория точки окружности катящейся по прямой линии. Наиболее распространены эвольвентные передачи.
Для косозубых цилиндрических передач изменяется выражения для нормальной силы в зацеплении, а также для длины линии контакта b . С учетом этого коэффициент становится равным 430 МПа1/3.
Для
расчетов по формуле (5.15) требуется знать
желаемое передаточное число, крутящий
момент, а также задать коэффициент
ширины зубчатого колеса , выбрать сталь для изготовления зубчатых
колес и определить для неё расчетное
контактное напряжение
, выбрать сталь для изготовления зубчатых
колес и определить для неё расчетное
контактное напряжение
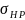 .
.
После
определения значения межосевого
расстояния
с помощью указанных выше зависимостей
определяют ширину зубчатого колеса,
выбирают модуль, рассчитывают числа
зубьев зубчатых колес и их диаметры.
Полученные значения изменяют расчетную
величину
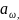 поэтому требуется проведение
проверочных расчетов, для чего используется
выражение (5.14), которое после некоторой
корректировки принимает вид:
поэтому требуется проведение
проверочных расчетов, для чего используется
выражение (5.14), которое после некоторой
корректировки принимает вид:
 (5.16)
(5.16)
Здесь
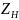 – коэффициент, учитывающий форму
рабочей поверхности зуба зубчатого
колеса (её кривизну). Он зависит от угла
наклона зуба β для косозубых передач и
коэффициента смещения инструмента x
при коррегировании зуба.
– коэффициент, учитывающий форму
рабочей поверхности зуба зубчатого
колеса (её кривизну). Он зависит от угла
наклона зуба β для косозубых передач и
коэффициента смещения инструмента x
при коррегировании зуба.
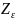 – коэффициент, учитывающий суммарную
длину линий контакта зубьев шестерни
и колеса в процессе зацепления. Он
зависит от среднего числа пар зубьев
шестерни и колеса, находящихся в контакте
(эта величина определяется коэффициентом
торцевого перекрытия
– коэффициент, учитывающий суммарную
длину линий контакта зубьев шестерни
и колеса в процессе зацепления. Он
зависит от среднего числа пар зубьев
шестерни и колеса, находящихся в контакте
(эта величина определяется коэффициентом
торцевого перекрытия
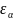 ) и увеличением длины линии контакта
зубьев для косозубых передач.
) и увеличением длины линии контакта
зубьев для косозубых передач.
Контрольные вопросы к лекции 5
Что такое контактные напряжения?
Какие разрушения зубчатых колес возникают от контактных напряжений?
Какие передачи рассчитываются по контактным напряжениям – закрытые или открытые?
Используя рис. 5.1 запишите выражение для нормальной силы в зацеплении через её тангенциальную составляющую и крутящий момент на зубчатом колесе.
Какой геометрический параметр в зубчатой передаче соответствует величине « » в формуле Герца?
Что означает величина
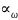 в зубчатой передаче?
в зубчатой передаче?Что означает коэффициент Ψbα ?
Найдите на рис. 3.1 радиусы кривизны шестерни и колеса.
От каких характеристик зубчатых колес зависит параметр в выражении 5.15?
Как определить ширину зубчатого колеса после получения значения величины межосевого расстояния по формуле 5.15?
Почему требуется проверочный расчет после проведения проектного расчета по формуле 5.15?
Что следует предпринять, если величина действующих контактных напряжений, полученная с помощью проверочного расчета по формуле 5.15 окажется большей чем заложенное в проектный расчет по формуле 5.14 допускаемое контактное напряжение?
Лекция №6
Тема лекции: Особенности геометрии и кинематики косозубых цилиндрических передач.
Прямозубые цилиндрические зубчатые передачи не рекомендуется использовать при окружных скоростях в зацеплении больших 2 метров в секунду. При более высоких скоростях появляются шумы, удары и вибрации в передаче, поэтому для работы при таких скоростях используются косозубые передачи.


На
рис. 6.1 позиция 1 изображено зубчатое
колесо на виде в направлении оси колеса.
Позиция 2 дает вид на это колесо сбоку
(слева). На этом виде зуб изображен
условно в виде линии наклоненной под
углом β к
образующей цилиндра, на котором нарезаны
зубья. Угол наклона зуба β обычно
принимают в интервале значений от 80
до 180.
Меньшие значения не дают больших
преимуществ по сравнению с прямозубыми
колесами, а значения большие 180
растут осевые силы в передаче, что
нагружает подшипниковые опоры, а также
уменьшается длина контактных линий
из-за пространственной кривизны зуба.
Если использовать раздвоенное зубчатое
колесо -3, в котором имеет место разное
направление наклона зуба на двух зубчатых
колесах, то осевые силы на них уравновешивают
друг друга и угол наклона зуба может
быть увеличен до 300
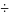 350.
350.
На рис.6.2 изображены зубья прямозубого колеса слева и косозубого – справа в двух проекциях. Верхняя проекция соответствует виду в направлении оси колеса (соответствует позиции 1 рис. 6.1), а нижняя проекция дает вид сбоку, что соответствует позиции 2рисунка 6.1. Косой зуб приобретает пространственную кривизну, что повышает его прочность на изгиб. Кроме того при одинаковой ширине прямозубого и косозубого колеса рабочая длина зуба косозубого колеса больше чем у прямозубого. Наклон зуба вызывает изменение кинематики косозубой передачи рис.6.3.
На рисунке представлены зубчатые колеса на виде сбоку. Слева прямозубое колесо, справа косозубое колесо. На колесах отмечены штриховыми линиями длины активных участков зацепления зубчатых колес gα. На этих участках происходит контакт зубьев шестерни и колеса при их вращении.

В позиции 1-1 у прямозубого колеса в зоне зацепления (работает) зуб 1. Зуб 2 в этот момент находится вне зоны зацепления (не работает). При вращении зубчатого колеса через некоторый момент времени зуб 1 выходит из зоны зацепления – позиция 1-2; а зуб 2 входит в зацепление. Таким образом, у прямозубого колеса постоянно в зацеплении один зуб.
Для косозубой передачи в положении 2-1 в зацеплении находится зуб 1, а зуб 2 не работает. В положении 2-2 зуб 1 выходит из зацепления, но не весь, а частично. Часть его продолжает работать. И в это же время зуб 2 тоже частично вошел в зацепление. Таким образом, в данный момент косозубая передача работает двумя парами зубьев. Это повышает нагрузочную способность передачи и делает её работу более плавной.

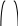


1 2
