
- •Лекция №1. Особенности математических вычислений, реализуемых на эвм.
- •Этапы решения математических задач на эвм
- •Погрешности решения математической задачи
- •Понятие устойчивости.
- •Лекция №2. Прямые методы решения систем линейных алгебраических уравнений. Метод Гаусса.
- •2.1. Классификация методов решения слау.
- •2.2. Метод Гаусса
- •Лекция №3. Прямые методы решения систем линейных алгебраических уравнений. Метод Жордана-Гаусса. Обращение матрицы.
- •3.1. Метод Жордана-Гаусса.
- •3.2. Обращение матрицы.
- •Лекция №4. Прямые методы решения систем линейных алгебраических уравнений. Метод прогонки. Примеры реализации.
- •Метод прогонки.
- •4.2. Примеры реализации.
- •5.1. Метод Якоби.
- •5.2. Метод Зейделя.
- •5.3. Метод верхней релаксации.
- •6.2. Сравнение методов.
- •7.1. Постановка задачи интерполяции.
- •7.2. Метод Лагранжа.
- •7.3. Интерполяционные формулы Ньютона.
- •8.2. Сплайн-интерполяция.
Лекция №2. Прямые методы решения систем линейных алгебраических уравнений. Метод Гаусса.
Продолжительность: 2 часа (90 мин.)
По оценкам специалистов до 75% задач вычислительной математики приходится на решение систем линейных алгебраических уравнений (СЛАУ). Современная вычислительная математика располагает значительным набором методов, позволяющих решать различные возникающие на практике линейные системы. Для того, чтобы выбрать наилучший способ решения практической задачи необходимо учитывать сильные и слабые стороны различных методов решения СЛАУ, знать границы их применимости, правильно оценивать их трудоемкость и устойчивость к вычислительным погрешностям.
2.1. Классификация методов решения слау.
Задача решения СЛАУ формулируется как вопрос численного решения систем вида:
 (2.1)
(2.1)
Или, в векторно-матричной форме:
![]() ,
,
где
![]() –
вектор правой части;
–
вектор правой части;
![]() –
вектор неизвестных;
–
вектор неизвестных;
![]() –
матрица коэффициентов системы.
–
матрица коэффициентов системы.
Все методы решения СЛАУ можно разделить на два класса: прямые и итерационные методы.
Прямые методы – используют конечные соотношения (формулы), которые приводят к решению за известное конечное число арифметических операций. Если арифметические операции реализуются точно, то и получаемое решение СЛАУ также будет точным.
Итерационные методы – это методы последовательных приближений к решению, получаемых путем повторения циклов вычислений, называемых итерациями. Результатом проведения итерации является получение очередного приближения к решению. Итерации проводятся до получения решения с заданной точностью. Объем вычислений при использовании методов данного класса заранее определить трудно.
Ч исленные
методы решения СЛАУ можно разделить на
две группы:
исленные
методы решения СЛАУ можно разделить на
две группы:
В качестве примера сопоставим трудозатраты для решения СЛАУ методом Крамера и методом Гаусса.
Пример: В методе Крамера количество операции (умножения) для решения СЛАУ размером n на n равно n!.
В методе Гаусса количество операций
(умножения) для решения СЛАУ размером
n на n равно
![]() .
.
Проведем оценку экономичности методов для разных размерностей СЛАУ:
для n=2
метод Крамера - n!=2
метод Гаусса - =8
для n=10
метод Крамера - n!=

метод Гаусса -

Из приведенных оценок видно, что метод Крамера лучше всего подходит для малых размерностей СЛАУ, начиная с размерности n=6 более эффективным становится метод Гаусса.
2.2. Метод Гаусса
Наиболее распространенным способом решения систем вида (2.1) является метод Гаусса. Суть данного метода состоит в последовательном исключении неизвестных.
Прямой ход метода Гаусса предполагает поэтапное приведение исходной системы СЛАУ к эквивалентной треугольной системе вида:
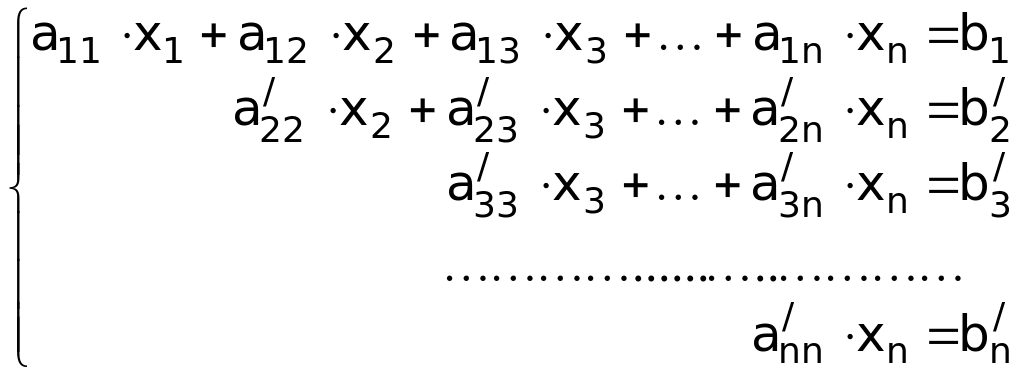 (2.2)
(2.2)
Затем, в ходе обратного хода метода
Гаусса, из n-ого уравнения
преобразованной системы (2.2), которое
содержит только один элемент вектора
неизвестных, находится значение
последнего коэффициента вектора
неизвестных -
![]() .
Подставляя полученное значение в
(n-1)-ое уравнение, которое
содержит два элемента вектора неизвестных,
находим значение
.
Подставляя полученное значение в
(n-1)-ое уравнение, которое
содержит два элемента вектора неизвестных,
находим значение
![]() и т.д., пока из 1-го уравнения не находим
значение
и т.д., пока из 1-го уравнения не находим
значение
![]() ,
полностью определив вектор неизвестных.
,
полностью определив вектор неизвестных.
На 1-ом этапе прямого хода метода Гаусса исходная система СЛАУ приводится к виду:
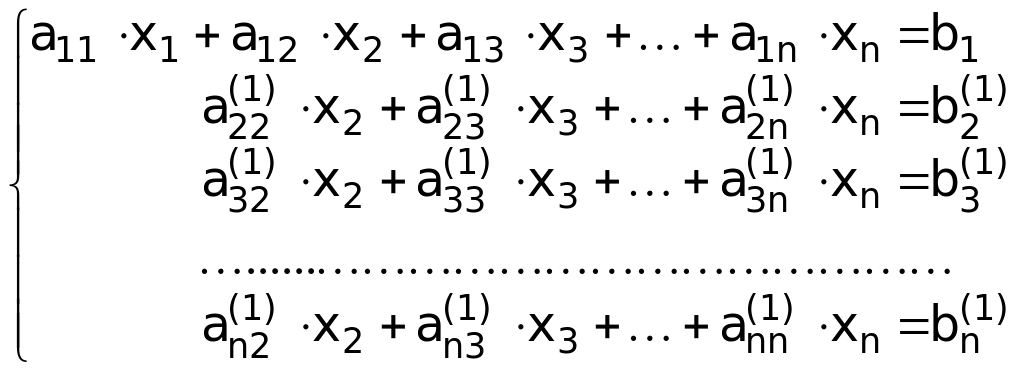 (2.3)
(2.3)
Коэффициенты
![]() системы
(2.3) вычисляются как результат эквивалентных
преобразований исходной системы (2.1).
системы
(2.3) вычисляются как результат эквивалентных
преобразований исходной системы (2.1).
Выпишем коэффициенты 1-ой и 2-ой строки исходной системы:
|
|
|
…, |
|
|
|
|
|
…, |
|
|
Разделим 1-ую строку на ее диагональный коэффициент:
|
|
|
…, |
|
|
Затем умножим 1-ую строку на первый коэффициент второй строки:
|
|
|
…, |
|
|
Далее вычитаем получившиеся коэффициенты 1-ой строки из коэффициентов 2-ой строки:
![]() ,
,
![]() ,
,
![]() ,
…,
,
…,
![]() ,
,
![]() .
.
Таким образом, формулы для преобразования элементов второй строки системы уравнений:
![]() ,
,
где
,
,
где
![]() .
.
Аналогичным образом выводим формулы для третьей и последующих строк:
![]() ,
,
![]() ,
,
…,
![]() ,
,
![]() ,
,
где .
Окончательные формулы для 1-го этапа прямого хода метода Гаусса:
![]() ,
,
![]() ,
,
где
![]() .
.
Второй этап прямого хода метода Гаусса.

Формулы для 2-го этапа прямого хода метода Гаусса:
 ,
,
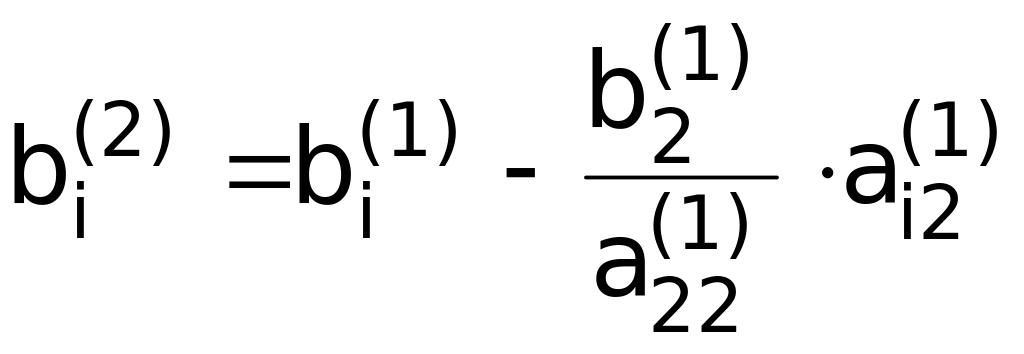 ,
,
где
![]() .
.
Этап (n-1) прямого хода метода Гаусса.

Формулы для (n-1)-го этапа прямого хода метода Гаусса:
 ,
,
 ,
,
здесь
![]() .
.
Таким образом, окончательная формула расчета коэффициентов СЛАУ для прямого хода метода Гаусса:
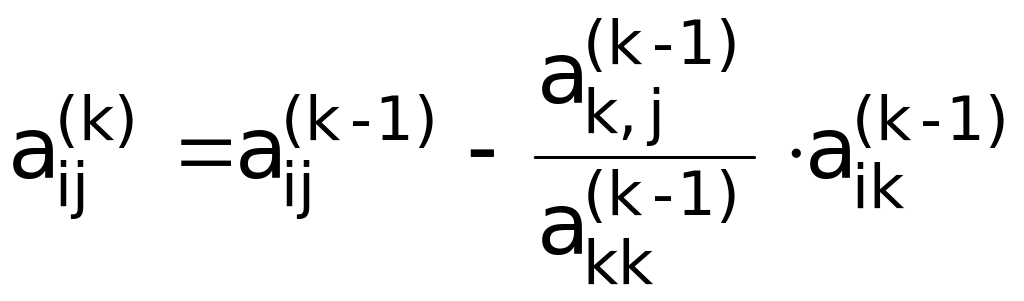 ,
,
 ,
,
где
![]()
![]() .
.
Обратный ход:
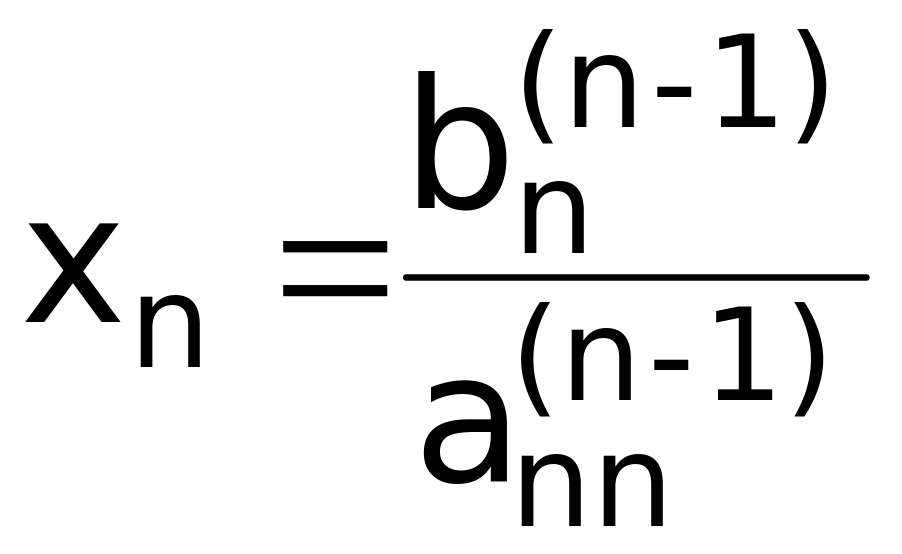 ;
;
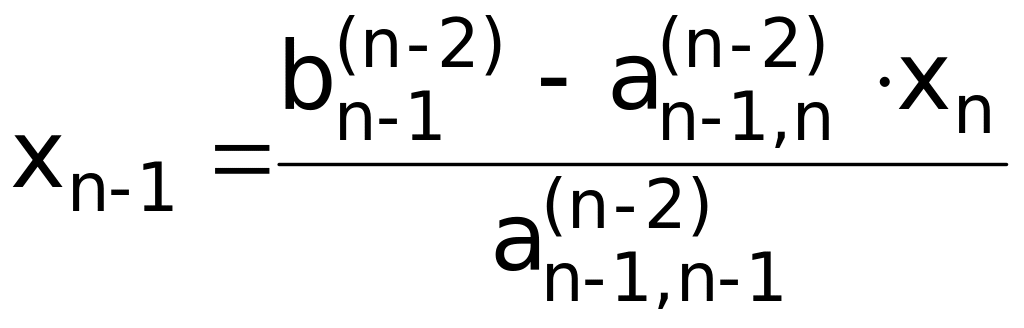 ;
;
……………
 ;
;
![]() .
.
Формула для обратного хода метода Гаусса:
 ,
,
где
![]() .
.
Алгоритм решения СЛАУ методом Гаусса:
Для
 :
:
2. Для
![]() :
:
3. ![]() ;
;
4. ![]() ;
;
5. Для
![]() :
:
6. ![]() ;
;
7.
![]() ;
;
8. Для
![]()
9. 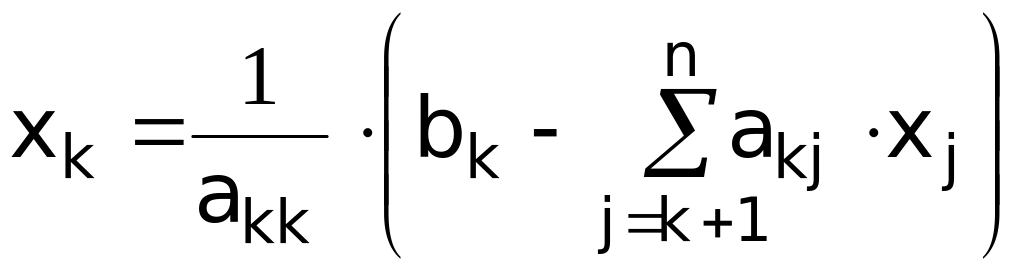 .
.
