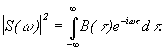Кафедра «Автоматика, телемеханика и связь»

ОБЩАЯ ТЕОРИЯ СВЯЗИ

Вопросы для подготовки к экзамену

1. Процессы передачи информации. Системы связи. Каналы связи

2. Сообщения, сигналы, помехи. Модуляция, кодирование

3. Сигналы, помехи как случайные процессы

4. Ковариационная функция, спектр случайного процесса

5. Теорема Винера-Хинчина

6. Корреляционный анализ детерминированных сигналов

7. Корреляционная функция модулированного сигнала

8. Описание сигналов во временной и частотной областях

9. Представление произвольного сигнала в виде суммы элементарных колебаний

10. Гармонический анализ периодических сигналов

11. Гармонический анализ непериодических сигналов

12. Математические модели сигналов

13. Пассивные, активные четырехполюсники, их частотные характеристики

14. Частотные характеристики резонансных цепей

15. Амплитудная модуляция. Спектр АМ-сигнала

16. Угловая модуляция. Спектр ЧМ-сигнала

17. Дискретная модуляция. Технологии DSL

18. Дискретно-разностные представления сигнала. Дельта-модуляция

19. Специальные виды модуляции: ШИМ, ФИМ

20. Цифровые виды модуляции. ИКМ

21. Дифференциальная ИКМ, адаптивная ИКМ

22. Двухступенчатая модуляция сигнала

23. Цифровые системы передачи. Преимущества и недостатки

24. Представление непрерывных сигналов отсчетами. Теорема Котельникова

25. Дискретизированный сигнал, его спектр

26. Математические модели каналов связи

27. Методы анализа прохождения сигналов через электрические цепи

28. Преобразование Гильберта, его использование для анализа прохождения сигналов

29. Амплитудно-частотная модуляция сигнала

30. Воздействие детерминированного сигнала на избирательную цепь. Аналитический сигнал

31. Определение огибающей сигнала на выходе избирательной цепи

32. Прохождение радиоимпульса через резонансный усилитель

33. Статистические характеристики узкополосного случайного процесса. Огибающая, частота, фаза процесса

34. Низкочастотная фильтрация с использованием модели прохождения сигнала через полосовую цепь

35. Оптимальная линейная фильтрация

36. Прием сигналов как статистическая задача. Потенциальная помехоустойчивость приема

37. Критерии качества и правила приема дискретных сообщений. Оптимальный приемник

38. Основы теории передачи информации. Измерение информации

39. Производительность, избыточность источника. Информационные параметры реальных источников

40. Теорема кодирования для канала с помехами

41. Помехозащищенные коды. Обнаруживающая и исправляющая способность кода

42. Блочные корректирующие коды. Линейные двоичные коды

43. Циклические двоичные коды

44. Многоканальные системы. Частотное, временное, фазовое разделение сигналов.

45. Многоканальная система с разделением сигналов по форме

46. Эффективность системы передачи информации

47. Защита информации в системах связи. Основы теории шифрования

Лектор к.т.н., доцент Б. И. Давыдов

Вопрос№1. Процессы передачи информации. Системы связи. Каналы связи

Основной задачей радиотехники является передача сообщения на расстояние. Расстояние разделяет отправителя и адресата, датчик команд и исполнительное устройство, исследуемый процесс и измерительный механизм, источник космического радиоизлучения и регистрирующий прибор радиотелескопа, различные блоки ЭВМ — словом, источник и потребитель информации.

Расстояние, на которое передается сообщение, может быть очень незначительным (передача команд в ЭВМ от одного блока к другому) или огромным (межконтинентальная или космическая связь). Передача сообщений осуществляется с помощью проводных, кабельных, волноводных линий или в свободном пространстве. Естественно, что для передачи сигналов целесообразно использовать те физические процессы, которые имеют свойство перемещаться. К числу таких процессов относятся применяемые в радиотехнике электромагнитные колебания — радиоволны.

Совокупность сведений, подлежащих передаче, называется информацией. Сведения могут быть представлены в различной форме, зависящей от используемых знаков (символов), являющихся условными обозначениями некоторых элементарных знаний. Совокупность символов, содержащих некоторую информацию, называют сообщением, т. е. сообщение является формой, в которой информация передается от одного объекта (источника) к другому объекту (получателю).

Сигналом называют физический процесс, параметры которого зависят от передаваемых сообщений. Под системой связи понимают совокупность технических средств, предназначенных для передачи информации, включая источник сообщений и получателя сообщений.

В общем случае под каналом передачи информации понимают всю совокупность технических средств, обеспечивающих передачу электрических сигналов от источника сообщений к потребителю.

Рис. 6.1. Обобщенная схема системы передачи информации

Вопрос№2. Сообщения, сигналы, помехи. Модуляция, кодирование.

Совокупность символов, содержащих некоторую информацию, называют сообщением, т. е. сообщение является формой, в которой информация передается от одного объекта (источника) к другому объекту (получателю).

Передача сообщений, а, следовательно, и информации осуществляется при помощи сигналов. Сигналом называют физический процесс, параметры которого зависят от передаваемых сообщений.

Кроме излученного сигнала на антенну приемника поступают сигналы от посторонних источников и создают помехи приему полезного сигнала. Природа помех многообразна. Внешними мешающими помехами могут быть естественные электромагнитные процессы, происходящие в атмосфере, ионосфере, космосе, а также сигналы других радиотехнических систем. К внутренним помехам относятся флуктуационные шумы приемника, нестабильности питающих напряжений и параметров элементов приемника.

В большинстве случаев помехи складываются на входе приемника с полезным сигналом и поэтому называются аддитивными.

Модулятор преобразует первичный сигнал  в радиосигнал . Преобразование заключается в изменении одного или нескольких параметров  сигнала несущей частоты в соответствии c изменением модулирующего сигнала. Совокупность операций превращения сообщения  в радиосигнал  составляет способ передачи информации. Кодер (кодирующее устройство) служит для преобразования сообщения  в первичный электрический сигнал , который подается на модулятор. Кодирование заключается в сопоставлении последовательности символов источника определенным образом сформированной последовательности символов кодера [9, 36].

В узком смысле кодирование представляет собой преобразование дискретного сообщения в последовательность кодовых символов, осуществляемое по определенному правилу (в широком смысле под кодированием понимают любое преобразование сообщения в сигнал путем установления взаимного соответствия). Множество всех кодовых последовательностей (кодовых комбинаций), возможных при данном правиле кодирования, образует код. Совокупность символов, из которых составляются кодовые последовательности, называют кодовым алфавитом, а их число (объем кодового алфавита) – основанием кода. Число символов в кодовой комбинации может быть одинаковым или разным. Соответственно различают равномерные и неравномерные коды. Число символов в кодовой комбинации равномерного кода называется длиной кода. Из-за простоты реализации наибольшее распространение получил код с основанием 2 (двоичный код), имеющий в алфавите два символа: 0 и 1. Последовательности кодовых символов на выходе кодера называются кодовыми комбинациями или кодовыми словами.

Вопрос№3. Сигналы, помехи как случайные процессы.

http://sernam.ru/book_tec.php?id=17

Случайные сигналы и помехи относятся к случайным явлениям природы, изучением основных закономерностей которых занимается теория вероятностей. Все случайные явления, изучаемые в теории вероятностей, можно разбить на три типа: случайные события, случайные величины и случайные процессы. Каждый из этих типов случайных явлений имеет свои особенности и характеристики.

Случайные события. Случайное событие – это всякий факт, который в результате опыта может произойти или не произойти. Это и передача текста без ошибок, и работа канала связи без повреждений не менее  часов, и превышение помехой заданного уровня и т. д. Обозначаются случайные события начальными прописными буквами латинского алфавита: .

Случайные величины. Величина, которая принимает то или иное значение, заранее неизвестно какое именно, называется случайной. Число ошибок в тексте, число занятых каналов многоканальной системы связи, уровень помехи в канале, мощность сигнала на выходе линии связи – это все примеры случайных величин (СВ). Будем обозначать СВ прописными буквами латинского алфавита , а значения, которые они принимают, – строчными буквами .

СВ делятся на дискретные и непрерывные. Дискретная случайная величина  может принимать только конечное множество значений , непрерывная – любые значения  из некоторого интервала, даже бесконечного. Для математического описания СВ вводятся следующие неслучайные основные статистические характеристик.

Важнейшими числовыми характеристиками СВ являются математическое ожидание

,                                 (1.43)

дисперсия

                        (1.44)

и среднее квадратическое отклонение . Обобщением числовых характеристик являются начальные моменты распределения СВ

                              (1.45)

и центральные моменты

.                       (1.46)

Напомним, что , а числа   и  называются коэффициентами асимметрии и эксцесса. Ряд часто встречающихся в  статистической радиотехнике распределений и соответствующих числовых характеристик СВ приведены в табл. 1.2.

Вопрос№4. Ковариационная функция, спектр случайного процесса .

http://bourabai.kz/signals/ts17.htm

Ковариационные функции. Частным случаем корреляционной функции является функция автоковариации (ФАК), которая широко используется при анализе сигналов. Она представляет собой статистически усредненное произведение значений центрированной случайной функции X(t)-m_x(t) в моменты времени t_i и t_j и характеризует флюктуационную составляющую процесса:

K_Х(t_i,t_j) = (x(t_i)-m_x(t_i)) (x(t_j)-m_x(t_j)) p(x_i,t_j; x_i,t_j) dx_i dx_j, (17.1.5)

В терминах теории вероятностей ковариационная функция является вторым центральным моментом случайного процесса. Для центрированных случайных процессов ФАК тождественна функции корреляции. При произвольных значениях m_x ковариационные и корреляционные функции связаны соотношением:

K_X(t,t+) = R_X(t,t+) - m_x²(t).

Нормированная функция автоковариации (функция корреляционных коэффициентов):

_Х(t,t+) = K_Х(t,t+)/[(t)(t+)]. (17.1.6)

При = 0 значение _Х равно 1, а ФАК вырождается в дисперсию случайного процесса:

K_Х(t) = D_Х(t).

Отсюда следует, что для случайных процессов и функций основными характеристиками являются функции математического ожидания и корреляции (ковариации). Особой необходимости в отдельной функции дисперсии не имеется.

 

Рис. 17.1.7. Реализации и ковариационные функции случайных процессов.

Вопрос№5. Теорема Винера-Хинчина.

http://dic.academic.ru/dic.nsf/enc_physics/3153/%D0%92%D0%98%D0%9D%D0%95%D0%A0%D0%90

ВИНЕРА-ХИНЧИНА ТЕОРЕМА

-утверждение о том, что спектральная плотность стационарного случайного процесса , связанная с его корреляц. ф-цией преобразованием Фурье:

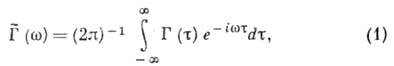
неотрицательна, О (угловые скобки означают статистич. усреднение, * - комплексное сопряжение). Спектральную плотность наз. также спектром мощности случайного процесса. В.-X. т. получена H. Винером (N. Wiener) в 1930, в иной формулировке - А. Я. Хинчиным в 1934.

Неотрицательность спектральной плотности позволяет трактовать этувеличину (при ) как меру интенсивности флуктуации случайного процесса на частоте . Такая трактовка становится очевидной, если заметить, что спектральная плотность связана со случайным спектром

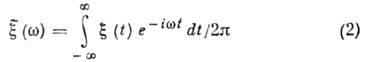
соотношением , где - дельта функция. Это наглядное соотношение непосредственно вытекает из (1) и (2) и при теоретич. анализе обычно позволяет получать правильные следствия, однако оно является чисто формальным, т. к. отд. реализации стационарного процесса , вообще говоря, не исчезают при и спектр (2) в обычном смысле не существует. Чтобы обойти эту трудность, достаточно рассмотреть вместо (2) спектр "обрезанных" реализаций:

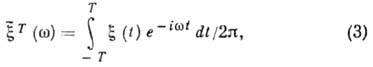
к-рый при больших T можно трактовать как нек-рую аппроксимацию (2). Из (1) и (3) следует, что для стационарного процесса т. е. спектральная плотность пропорциональна ср. квадрату амплитуды случайного спектра

Спектральная плотность служит одним из осн. понятий при корреляц. анализе случайных ф-ций в статистич. радиофизике, в теории равновесных тепловых флуктуации, в физ. кинетике и др. и допускает непо-средств. обобщение на статистически однородные и стационарные случайные поля, переходя в пространственно-временной спектр случайного поля.

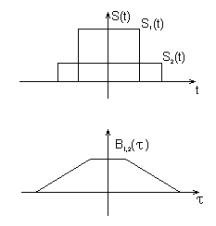
Вопрос№6. Корреляционный анализ детерминированных сигналов

     Корреляционный анализ - это анализ временной зависимости сигналов.

Взаимно-корреляционная функция

     Для оценки степени связи во времени между двумя различными сигналами  и  используется взаимно-корреляционная функция ВКФ. 

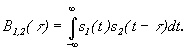
Найдем спектральную плотность ВКФ. Для этого рассмотрим сначала спектральную плотность произведения двух функций  Каждой из функций сомножителей соответствуют спектральные плотности  и  Согласно теореме о спектральной плотности произведения двух функций,

С другой стороны, согласно общей формуле определения спектральной плотности

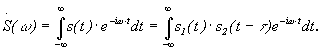
Положим в обеих формулах w = 0, получим:

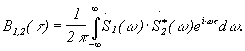
Итак, согласно общему интегральному представлению спектра сигнала спектральная плотность для ВКФ равна произведению спектральной плотности одной функции на сопряженную спектральную плотность другой.

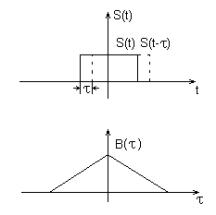
Автокорреляционная функция сигнала (АКФ)

     АКФ - это степень связи сигнала s(t) с его копией, сдвинутой на величину t.

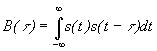,  при t = 0

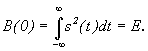
Максимальное значение автокорреляционной функции (при t = 0) равно энергии сигнала, т. к. сигнал полностью коррелирован сам с собой. Полагая в преобразовании Фурье взаимнокорреляционной функции  получим: ,

При t = 0 получим равенство Парсеваля .

     Итак, в частотной области имеется две характеристики сигнала: спектральная плотность и спектральная плотность энергии.

     Спектральной плотности , содержащей полную информацию о сигнале, соответствует в преобразовании Фурье сам сигнал s(t). Спектральной плотности энергии сигнала , лишенной фазовой информации, в преобразовании Фурье соответствует автокорреляционная функция сигнала .

     Для периодических функций энергия бесконечна, поэтому автокорреляционная функция определяется путем усреднения по периоду:

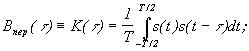
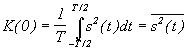 - средняя мощность сигнала.

В более общем случае не обязательно периодического, но с бесконечной полной энергией сигнала принимают:

.

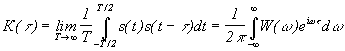Фурье образом такой автокорреляционной функции будет спектральная плотность мощности W(w), что видно из соотношения 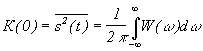. Формально

     Однако практически спектральная плотность мощности определяется через функцию автокорреляции

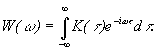
Пример. Автокорреляционная функция прямоугольного импульса

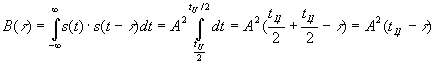 при

Вопрос№7. Корреляционная функция модулированного сигнала

Корреляционная функция модулированного колебания

При нахождении корреляционной функции модулированного колебания будем исходить из условия абсолютной интегрируемости функции (сигнал с конечной энергией), что позволяет применять определение (см. § 2.18)

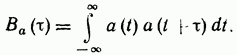(3.101)

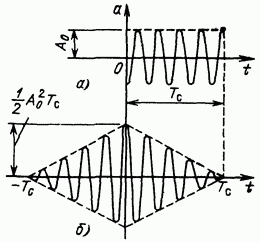
Рис. 3.30. Импульс с высокочастотным заполнением (а) и корреляционная функция (б)

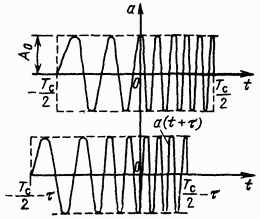
Рис. 3.31. К построению корреляционной функции ЛЧМ импульса

Вычисление интеграла для сложных сигналов требует громоздких выкладок. Задача существенно упрощается при переходе от колебания a(t) к аналитическому сигналу . Основываясь на соотношениях, выведенных в предыдущем параграфе, рассмотрим сначала чисто амплитудную модуляцию, когда и, следовательно,

Тогда формула (3.97) принимает вид

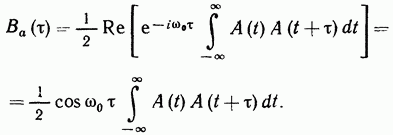(3.102)

Обозначив, как и в выражении (3.97), интегральный множитель через , окончательно получим

(3.103)

Второй множитель есть корреляционная функция гармонического колебания с частотой и единичной амплитудой.

Итак, корреляционная функция амплитудно-модулированного радиосигнала равна произведению корреляционных функций огибающей и высокочастотного заполнения.

В качестве примера на рис. 3.30, а показан радиоимпульс с прямоугольной огибающей, а на рис. 3.30, б — соответствующая этому импульсу корреляционная функция. Следует отметить, что эта функция не зависит от начальной фазы заполнения радиоимпульса, а ее огибающая совпадает с корреляционной функцией прямоугольного видеоимпульса (см. § 2.18, рис. 2.36, г).

Для иллюстрации применения общего выражения (3.99) к амплитудно-частотной модуляции найдем корреляционную функцию импульса, изображенного на рис. 3.19, а.

При обозначениях формулы (3.37) и рис. 3.19 аналитический сигнал запишется в виде

(3.104)

Применяя формулы (3.94) и (3.97), получаем

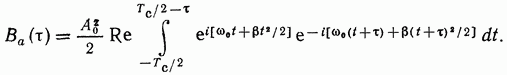(3.105)

Пределы интегрирования взяты с учетом условия одновременного существования функций (рис. 3.31).

С помощью несложных преобразований выражение (3.105) приводится к виду

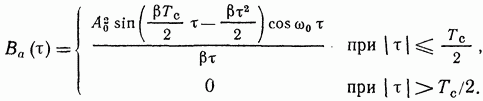(3.106)

Используя введенный в § 3.7 параметр [см. (3.38)] и учитывая, что приводим выражение (3.106) к более общему виду

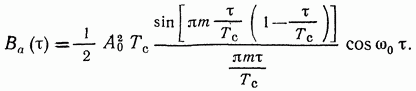(3.106)

Множитель равен полной энергии рассматриваемого радиоимпульса (как и при импульсе с постоянной частотой заполнения, см. рис. 3.30, б).

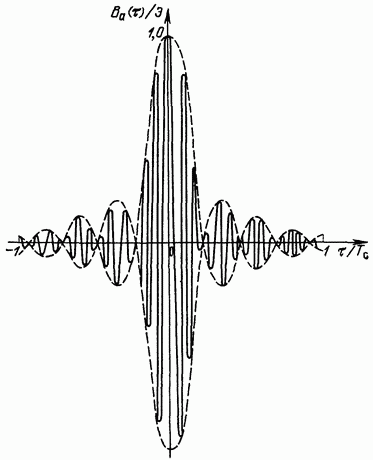
Рис. 3.32. Корреляционная функция ЛЧМ импульса

Таким образом,

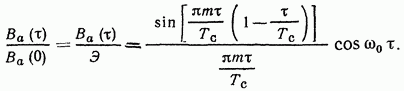
График этой функции построен на рис. 3.32 для параметра в предположении, что очень велико (масштаб выбран произвольно). Огибающая корреляционной функции образует весьма острый пик (при m > 1), а частота заполнения постоянна и равна центральной частоте исходного радиоимпульса.

Рассмотренный здесь сигнал с большой базой m и его корреляционная функция представляют большой практический интерес для современной радиотехники.

Вопрос№8. Описание сигналов во временной и частотной областях.

Сигналы, отображаемые во временной области

Во временной области зависимость уровня электрических сигналов в функции от времени обычно наблюдают с помощью осциллографа. Для наглядного представления сигналов различной формы целесообразно использовать векторные проекции (диаграммы). Соответствие между этими двумя способами представления сигналов отражено на рисунке 1 на примере простого синусоидального сигнала.

 

 

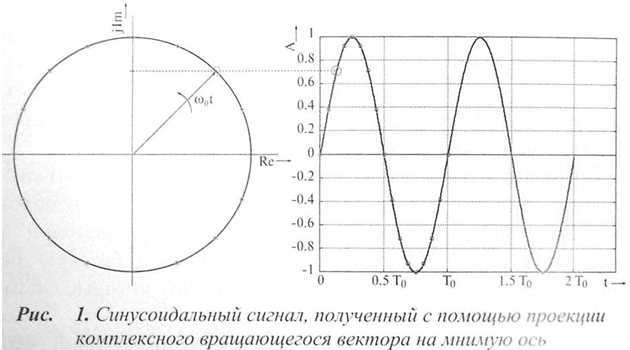
Уровень сигнала в функции от времени соответствует проекции вектора на мнимую ось комплексной плоскости. Угловая частота вектора находится как

ω₀=2πf₀ (1.1)

где, ω₀- угловая частота, рад/сек; f₀- частота сигнала, Гц.

Синусоидальный сигнал x(t)=Аsin(2πf₀ t) можно записать в виде: x(t)=АIm[ej2πf₀ t ]

Сигналы, отображаемые в частотной области.

Что такое спектр? Так чем же является спектр в контексте нашего обсуждения? Спектр – это набор синусоидальных волн, которые, будучи надлежащим образом скомбинированы, дают изучаемый нами сигнал во временной области. На Рис. 1-1 показана волновая форма сложного сигнала. Давайте предположим, что мы ожидали увидеть чисто синусоидальный сигнал. И хотя форма явно демонстрирует нам, что сигнал не является чистой синусоидой, она не дает определенного ответа на вопрос о причинах данного явления. На Рис. 1-2 показан наш сложный сигнал во временной и в частотной области. В частотной области показана амплитуда для каждой синусоидальной волны в спектре в зависимости от частоты. Как видно, в данном случае спектр состоит лишь из двух волн. Теперь мы знаем, отчего наш сигнал не является чистой синусоидой: в нем содержится еще одна волна, вторая гармоника в нашем случае. Означает ли это, что измерения во временной области можно вообще не проводить? Отнюдь. Временная область является предпочтительной для многих измерений, а для некоторых является единственно возможной. К примеру, только во временной области можно измерить длительность фронта и спада импульса, выбросы и биения.

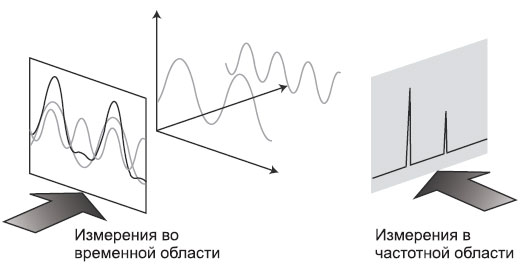
Рисунок 1-2. Связь между временной и частотной областью

Для чего измерять спектр? У частотной области есть свои плюсы в плане измерений. Мы уже видели на Рис. 1-1 и 1-2, что частотная область гораздо удобнее для определения гармонического состава сигнала. Те, кто занимаются беспроводной связью, очень заинтересованы в определении внеполосного и паразитного излучения. Например, сотовые радиосистемы должны проверяться на наличие гармоник несущего сигнала, которые могут вносить помехи в работу других систем, оперирующих на той же частоте, что и гармоники. Инженеры и техники также часто обеспокоены искажением сообщений, транслирующихся с модуляцией несущего сигнала. Интермодуляция третьего порядка (то есть две составляющие сложного сигнала, модулирующие друг друга) может причинить много хлопот, поскольку компоненты искажения могут попасть в интересуемую полосу частот и не будут надлежащим образом отфильтрованы. Наблюдение за спектром – еще одна важная сторона измерений в частотной области. Государственные регулирующие структуры распределяют различные частоты для различных радио-служб: телевизионное и радиовещание, сотовая связь, связь правоохранительных органов и спасательных служб, а также множество иных организаций и приложений. Крайне важно, чтобы каждая служба работала только на предназначенной для нее частоте и оставалась в пределах выделенной полосы канала. Передатчики и другие излучатели зачастую могут работать на очень близко расположенных соседних частотах. Для усилителей мощности и других компонентов таких систем ключевым параметром для измерения является количество энергии сигнала, просачивающейся в соседние каналы и порождающей интерференцию. Электромагнитная интерференция (EMI) – это термин, применяемый к нежелательному излучению от преднамеренных и случайных излучателей. Поводом для беспокойства тут служит тот факт, что это нежелательное излучение, будучи передано в эфир или по проводам, может затруднить работу других систем. При разработке и производстве практически любой электрической или электронной продукции необходимо исследовать уровни излучения в зависимости от частоты, и приводить их в соответствие с нормами, устанавливаемыми правительственными органами или индустриальными стандартами.

Вопрос№9. Представление произвольного сигнала в виде суммы элементарных колебаний.

В математике доказывается, что если функции ф_n(x) непрерывны, то произвольная кусочно-непрерывная функция f(x), для которой выполняется условие

может быть представлена в виде суммы ряда

(1)

Интеграл в предыдущем выражении вычисляется по области определения f(x).

коэффициенты Фурье

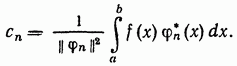(2)

Подставляя (2) в (1), получаем обобщенный ряд Фурье по данной системе.

Обобщенный ряд Фурье обладает следующим важным свойством: при заданной системе функций ф_n(x) и фиксированном числе слагаемых ряда (1)он обеспечивает наилучшую аппроксимацию (в смысле минимума среднеквадратической ошибки) данной функции .

Применительно к сигналам s(t), являющимся функциями времени, выражение (2.8) в дальнейшем будет записываться в форме

В новых обозначениях квадрат нормы функции s(t) по аналогии с (2.6) будет

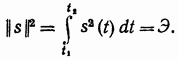
Таким образом, в соответствии с формулой

энергия сигнала

Вопрос№10. Гармонический анализ периодических сигналов.

При разложении периодического сигнала s(t)в ряд Фурье по тригонометрическим функциям в качестве ортогональной системы берут

(1)

или

(2)

Интервал ортогональности в обоих случаях совпадает с периодом функции s(t). Система функций (1)приводит к тригонометрической форме ряда Фурье, а система(2)— к комплексной форме. Между этими двумя формами существует простая связь.

Косинусная (действительная) и синусная (мнимая) части коэффициента определяются формулами

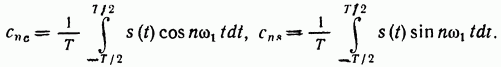
Коэффициенты С_n часто бывает удобно записывать в форме

где

(2.27)

В математической и радиотехнической литературе часто встречается следующая форма записи:

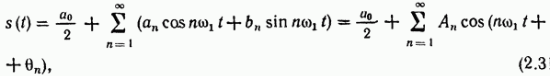
Вопрос№11. Гармонический анализ непериодических сигналов.

Выделив произвольный отрезок времени Т, включающий в себя промежуток мы можем представить заданный сигнал в виде ряда Фурье.

где , а коэффициенты в соответствии с формулой (2.22)

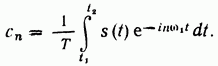
Подставив (2.44) в (2.43), получим

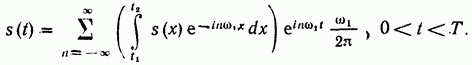
Здесь учтено, что

Вне отрезка ряд (2.43) определяет функцию где k — целое число, т. е. периодическую функцию, полученную повторением s(t) вправо и влево с периодом Т. Для того чтобы вне отрезка функция равнялась нулю, величина Т должна быть бесконечно большой. Но чем больше отрезок Т, выбранный в качестве периода, тем меньше коэффициенты . Устремляя Т к бесконечности, в пределе получаем бесконечно малые амплитуды гармонических составляющих, сумма которых изображает исходную непериодическую функцию , заданную в интервале (см. рис. 2.11). Число гармонических составляющих, входящих в ряд Фурье, будет при этом бесконечно большим, так как при основная частота функции . Иными словами, расстояние между спектральными линиями (см. рис. 2.2), равное основной частоте становится бесконечно малым, а спектр — сплошным.

Поэтому в выражении (2.45) можно заменить на на текущую частоту , а операцию суммирования операцией интегрирования.

Таким образом, приходим к двойному интегралу Фурье

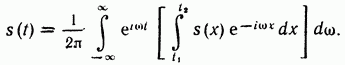
Внутренний интеграл, являющийся функцией ,

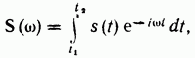
называется спектральной плотностью или спектральной характеристикой функции s(t).

В общем случае, когда пределы и не уточнены, спектральная плотность записывается в форме

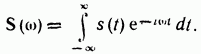
После подстановки (2.48) в выражение (2.46) получаем

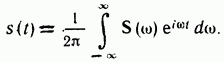
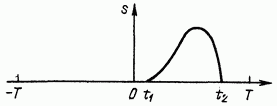
Рис. 2.11. Одиночный импульс

Выражения (2.48) и (2.49) называются соответственно прямым и обратным преобразованиями Фурье.

Выражение (2.48) отличается от (2.22) только отсутствием множителя 1/Т. Следовательно, спектральная плотность обладает всеми основными свойствами коэффициентов комплексного ряда Фурье. По аналогии с (2.23) и (2.25) можно написать

где

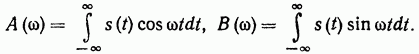
Модуль и аргумент спектральной плотности определяются выражениями

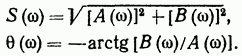(2.53)

Первое из этих выражений можно рассматривать как амплитудно-частотную (АЧХ), а второе — как фазо-частотную характеристики (ФЧХ) сплошного спектра непериодического сигнала s(t).

Как и в случае ряда Фурье, является четной, а — нечетной функцией частоты .

На основании формулы (2.50) нетрудно привести интегральное преобразование (2.49) к тригонометрической форме. Имеем [аргумент функции в последующих выражениях опущен]:

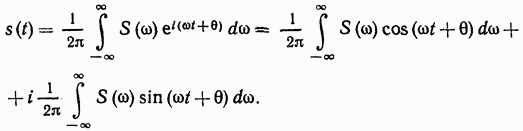
Из четности модуля и нечетности фазы следует, что подынтегральная функция в первом интеграле является четной, а во втором — нечетной относительно со. Следовательно, второй интеграл равен нулю и окончательно

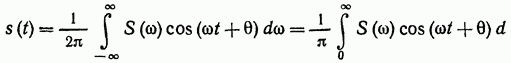(2.54)

Переход от комплексной формы (2.49) к тригонометрической (2.54) обычно целесообразен в конце анализа; все промежуточные выкладки при применении интеграла Фурье удобнее и проще производить на основании комплексной формы (2.49).

Отметим, что при выражение (2.47) переходит в следующее:

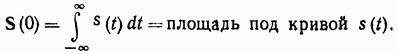
Следовательно, для любого сигнала s(t) спектральная плотность на нулевой частоте равна «площади сигнала». Это правило полезно для быстрого выявления структуры спектра некоторых сигналов. Примеры применения этого правила приводятся в § 2.10.

Вопрос№12. Математические модели сигналов.

Чаще всего сигнал электросвязи можно рассматривать как меняющуюся во времени электрическую величину (напряжение, ток, электромагнитное колебание, напряженность поля). Эти величины можно наблюдать и регистрировать с помощью различных приборов, например осциллографов. После наблюдения сигнал будет задан в виде графика или таблицы как функция времени. Такое представление называется временной диаграммой. В качестве примера можно привести осциллограмму тока, протекающего через микрофон.

 

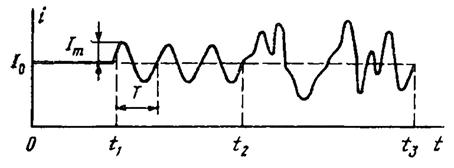
Временная диаграмма тока через микрофон.

На интервале звуковые колебания на микрофон не воздействовали; на интервале – воздействовало звуковое колебание определенного тона; на интервале – сложные звуковые колебания.

Однако временные диаграммы сигнала являются неудобными как для теоретических расчетов, так и для представления длительных сигналов. Поэтому для проведения всевозможных расчетов с сигналами возникает задача их математического описания. Оно заключается в получении такого относительно простого математического выражения (формулы, уравнения, неравенства и т.д.), по которому можно было бы вычислить необходимые свойства и параметры сигналов (мгновенные значения, числовые характеристики и т.п.). Математическое описание сигнала называется его математической моделью.

Классы сигналов и их математическое представление.

Разделение сигналов на классы производится по следующим признакам:

- форме – простые и сложные;

- информативности – детерминированные и случайные;

- характеристикам – непрерывные, дискретные и цифровые.

 

Математической моделью простого сигнала является простая функция времени. Из простых сигналов в электросвязи находят применение гармонические сигналы, конечные и бесконечные последовательности прямоугольных импульсов, испытательные сигналы и др.

Гармонический сигнал, который часто называют гармоническим колебанием, записывается в виде

 

при ,

 

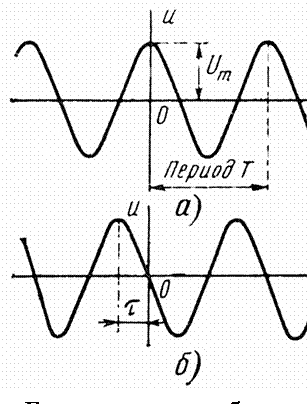где – максимальное значение (амплитуда); – циклическая частота; – начальная фаза. Сдвиг по фазе приводит к сдвигу гармонического колебания на время влево. Начальная фаза , циклическая частота . Часто при расчетах используется угловая частота .

 

 

Импульсными сигналами являются сигналы, отличные от нуля в течение ограниченного времени. Эти сигналы существуют лишь в пределах конечного отрезка . При этом различают видеоимпульсы и радиоимпульсы.

 

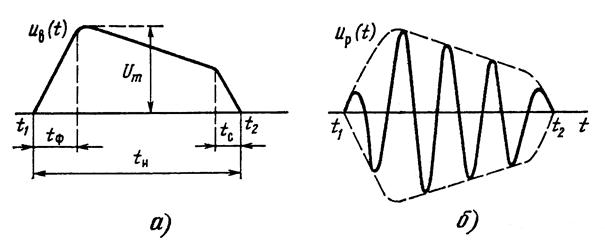
Импульсные сигналы: а) – видеоимпульс; б) – радиоимпульс.

 

Если – видеоимпульс, то соответствующий ему радиоимпульс (частота и начальная фаза могут быть произвольными). В радиоимпульсе называется огибающей, а функция – заполнением. Параметры видеоимпульса: – амплитуда; – длительность импульса; – длительность фронта импульса; – длительность спада импульса. Происхождение термина «видеоимпульс» связано с тем, что впервые такие импульсы начали применять для описания сигналов в телевидении.

В электросвязи наибольшее применение находят одиночные импульсы или их периодическая последовательность, форма которой приближается к прямоугольной. Для периодической последовательности импульсов, кроме перечисленных параметров, вводится понятие скважности, определяемой как отношение периода к длительности импульса:

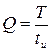
Бесконечно короткий видеоимпульс бесконечной амплитуды называется δ – функцией (дельта – функция), которая записывается в виде:

 

 

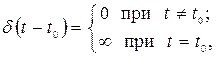
где – момент действия импульса. Эта функция обладает следующим свойством:

,

физически означающим, что хотя значение δ – функции в точке и равно бесконечности, но площадь ее конечна и единична.

Широко используется δ – функция при анализе различных радиотехнических цепей. Она является математической моделью прямоугольного импульса малой длительности и большой амплитуды.

Сложные сигналы представляют собой такие функции времени, которые трудно выразить в виде простой математической формулы. Например – отрезок речевого сигнала. Большинство реальных сигналов – это сложные сигналы. Возникает вопрос, как же для них подобрать приемлемое математическое выражение, причем желательно такое, которое подходило бы для большинства сигналов?

Математиками найдено такое решение. Им широко пользуются в электро– и радиотехнике. Сигнал можно представить в виде ряда некоторых элементарных (простых) функций , называемых базисными:

,

где – коэффициенты разложения, зависящие от сигнала .

Выбор системы базисных функций зависит от вида сигнала и решаемой задачи. Но имеется общее правило – функции сами должны быть простыми, обеспечивать простое вычисление коэффициентов и давать хорошую сходимость ряда к сигналу . Выбор функции считается тем лучше, чем меньше требуется составляющих ряда для представления сигнала с заданной точностью:

 

.

 

Детерминированные и случайные сигналы.

Детерминированным является сигнал, задаваемый функцией времени, по которой можно вычислить его мгновенные значения в любые моменты. Примерами таких сигналов являются гармоническое колебание, видеоимпульсы с известными параметрами. Детерминированные сигналы используются в технике связи как контрольные, испытательные и в качестве переносчика (несущей) для получения модулированных сигналов.

Случайным называется сигнал, математическим описанием которого является случайная функция времени. Физически сигнал можно считать случайным, если невозможно определенно предсказать или вычислить его мгновенные значения. Помехи системы связи чаще всего являются случайными. Сигналы же, в зависимости от обстоятельств, могут быть и детерминированными, и случайными. Случайные сигналы не обязательно являются сложными, они могут быть и простыми.

 Непрерывные, дискретные и цифровые сигналы.

Сигналы, которые существуют непрерывно во времени и принимают любые значения из какого – то интервала называются непрерывными. Также непрерывные сигналы называются аналоговыми.

Первоначально в электросвязи использовались преимущественно аналоговые сигналы. Их можно просто генерировать, усиливать, передавать и принимать. Недостатком таких сигналов является то, что любое изменение их формы из – за помех и искажений влечет за собой изменение формы принимаемого сообщения. Возросшие требования к точности воспроизведения сообщений заставили перейти к дискретным и цифровым сигналам.

Дискретные сигналы – это сигналы, принимающие конечное число значений или состояний. Дискретные сигналы могут непосредственно создаваться на выходе преобразователя сообщение – сигнал или образовываться в результате дискретизации аналогового сигнала.

Цифровые сигналы – разновидность дискретных сигналов, когда квантованные отсчетные значения представлены в виде цифр. Цифровыми также являются сигналы, соответствующие кодовым комбинациям на выходе кодера. Преимущество цифровых сигналов – более высокая помехоустойчивость и возможность их формирования и обработки микроэлектронными логическими устройствами. Цифровые сигналы находят все большее применение в новых системах электросвязи.

 

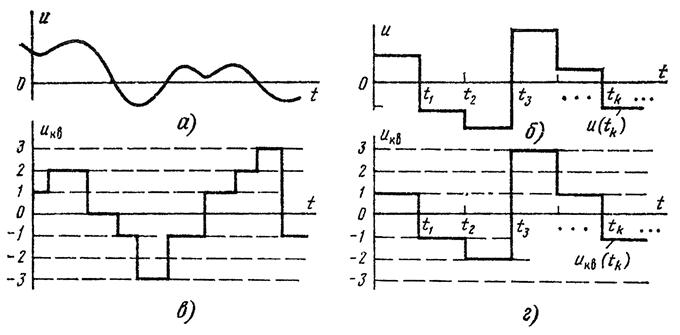
Сигналы: а) – непрерывные; б) – дискретные по времени; в) – квантованные по уровню и непрерывные по времени; г) – квантованные по уровню и дискретные по времени.

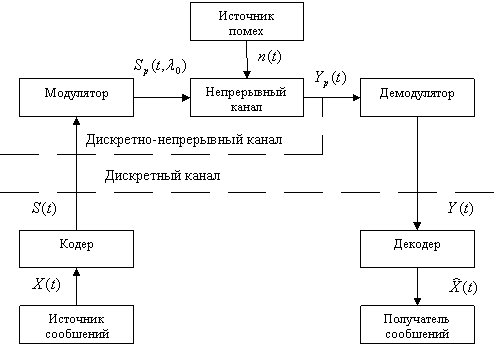
Вопрос№13. Пассивные, активные четырехполюсники, их частотные характеристики.

Четырёхпо́люсник — электрическая цепь, разновидность многополюсника, имеющая четыре точки подключения. Как правило, две точки являются входом, две другие — выходом.
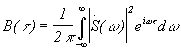