33. Ко́льца Нью́тона — кольцеобразные интерференционные максимумы и минимумы, появляющиеся вокруг точки касания слегка изогнутой выпуклой линзы и плоскопараллельной пластины при прохождении света сквозь линзу и пластину.

Классическое объяснение явления[править | править вики-текст]

Удовлетворительно объяснить, почему возникают кольца, Ньютон не смог. Удалось это Юнгу. Проследим за ходом его рассуждений. В их основе лежит предположение о том, что свет — это волны. Рассмотрим случай, когда монохроматическая волна падает почти перпендикулярно на плосковыпуклую линзу.

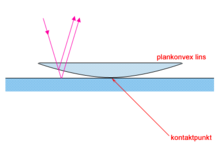
Рис. 1

Пример колец Ньютона

Волна 1 появляется в результате отражения от выпуклой поверхности линзы на границе стекло — воздух, а волна 2 — в результате отражения от пластины на границе воздух — стекло. Эти волны когерентны, то есть у них одинаковые длины волн, а разность их фаз постоянна. Разность фаз возникает из-за того, что волна 2 проходит больший путь, чем волна 1. Если вторая волна отстает от первой на целое число длин волн, то, складываясь, волны усиливают друг друга.

 — max, где -    любое целое число,    -  длина волны.

Напротив, если вторая волна отстает от первой на нечетное число полуволн, то колебания, вызванные ими, будут происходить в противоположных фазах и волны гасят друг друга.

 — min, где -    любое целое число,    -  длина волны.

Для учета того, что в разных веществах скорость света различна, при определении положений минимумов и максимумов используют не разность хода, а оптическую разность хода. Разность оптических длин пути называется оптической разностью хода.

 — оптическая длина пути,

 — оптическая разность хода.

Если известен радиус кривизны R поверхности линзы, то можно вычислить, на каких расстояниях от точки соприкосновения линзы со стеклянной пластиной разности хода таковы, что волны определенной длины λ гасят друг друга. Эти расстояния и являются радиусами темных колец Ньютона. Необходимо также учитывать тот факт, что при отражении световой волны от оптически более плотной среды фаза волны меняется на  , этим объясняется тёмное пятно в точке соприкосновения линзы и плоскопараллельной пластины. Линии постоянной толщины воздушной прослойки под сферической линзой представляют собой концентрические окружности при нормальном падении света, при наклонном — эллипсы. Радиус k-го светлого кольца Ньютона (в предположении постоянного радиуса кривизны линзы) в отражённом свете выражается следующей формулой:

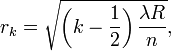
где

R — радиус кривизны линзы;

k = 1, 2, …;

λ — длина волны света в вакууме;

n — показатель преломления среды между линзой и пластинкой.

34. Применение интерференции.

Просветление оптики Просветление оптики, то есть создание покрытий на поверхности оптических деталей, в первую очередь линз, является одним из простейших и наиболее распространенных применений интерференции света. На поверхности линзы создаётся специальное покрытие. В таком случае волны, отраженные от границ раздела пленка-воздух и пленка-стекло будут складываться в противофазе и “гасить” друг друга. Для того чтобы это гашение было наиболее эффективным, необходимо дополнительно постараться уравнять амплитуды обеих отраженных волн. Это достигается подбором материала пленки. На практике удачным подбором материала пленки удается снизить коэффициент отражения поверхности в 20-100 раз по сравнению с исходной поверхностью стекла - для когерентного излучения данной длины волны. В случае когда падающий на поверхность свет не монохроматический, т.е. состоящий из света разных цветов (фотографические, микроскопические устройства), из вышеприведенной формулы очевидно, что обеспечить идеальное просветление для всех спектральных компонент невозможно. Поэтому просветление обычных бытовых фотообъективов и т.п. устройств выполняется в расчете на наилучшее просветление в области максимальной спектральной чувствительности глаза. Кроме того, существует техника создания многослойных просветляющих покрытий со слоями различной толщины, эффективно осуществляющих гашение отраженного света в достаточно широкой спектральной области. Принцип действия таких слоев тот же что и описанный выше - взаимное интерференционное гашение двух или нескольких волн, отраженных от границ раздела многослойного покрытия. Голография Ещё одним важным применением интерференции является голография. При голография представляет собой "трёхмерную фотографию". Смотря на голографию под разными углами вы сможете рассмотреть изображённый на ней предмет с разных сторон. Подробнее о голографии вы сможете узнать в 11 классе на факультативном курсе "Современная оптика". С помощью явления интерференции проверяют качество деталей, определяют показатель преломления различных сред и т.д.

35. Дифракцией света называется явление отклонения света от прямолинейного направления распространения при прохождении вблизи препятствий. Как показывает опыт, свет при определенных условиях может заходить в область геометрической тени. Если на пути параллельного светового пучка расположено круглое препятствие (круглый диск, шарик или круглое отверстие в непрозрачном экране), то на экране, расположенном на достаточно большом расстоянии от препятствия, появляется дифракционная картина– система чередующихся светлых и темных колец. Если препятствие имеет линейный характер (щель, нить, край экрана), то на экране возникает система параллельных дифракционных полос.

Принцип Гюйгенса является развитием принципа, который ввёл Христиан Гюйгенс в 1678 году: каждая точка фронта(поверхности, достигнутой волной) является вторичным (т.е. новым) источником сферических волн. Огибающая фронтов волн всех вторичных источников становится фронтом волны в следующий момент времени.

Принцип Гюйгенса объясняет распространение волн, согласующееся с законами геометрической оптики, но не может объяснить явлений дифракции. Огюстен Жан Френель в 1815 году дополнил принцип Гюйгенса, введя представления о когерентности и интерференции элементарных волн, что позволило рассматривать на основе принципа Гюйгенса — Френеля и дифракционные явления.

Принцип Гюйгенса — Френеля формулируется следующим образом:

Каждый элемент волнового фронта можно рассматривать как центр вторичного возмущения, порождающего вторичные сферические волны, а результирующее световое поле в каждой точке пространства будет определяться интерференцией этих волн.

36. Метод зон Френеля Френель предложил метод разбиения фронта волны на кольцевые зоны, который впоследствии получил название метод зон Френеля.

Пусть от источника света S распространяется монохроматическая сферическая волна, P - точка наблюдения. Через точку O проходит сферическая волновая поверхность. Она симметрична относительно прямой SP.

Разобьем эту поверхность на кольцевые зоны I, II, III и т.д. так, чтобы расстояния от краев зоны до точки P отличались на l/2 - половину длины световой волны. Это разбиение было предложено O. Френелем и зоны называют зонами Френеля.

Возьмем произвольную точку 1 в первой зоне Френеля. В зоне II найдется, в силу правила построения зон, такая соответствующая ей точка, что разность хода лучей, идущих в точку P от точек 1 и 2 будет равна l/2. Вследствие этого колебания от точек 1 и 2 погасят друг друга в точке P.

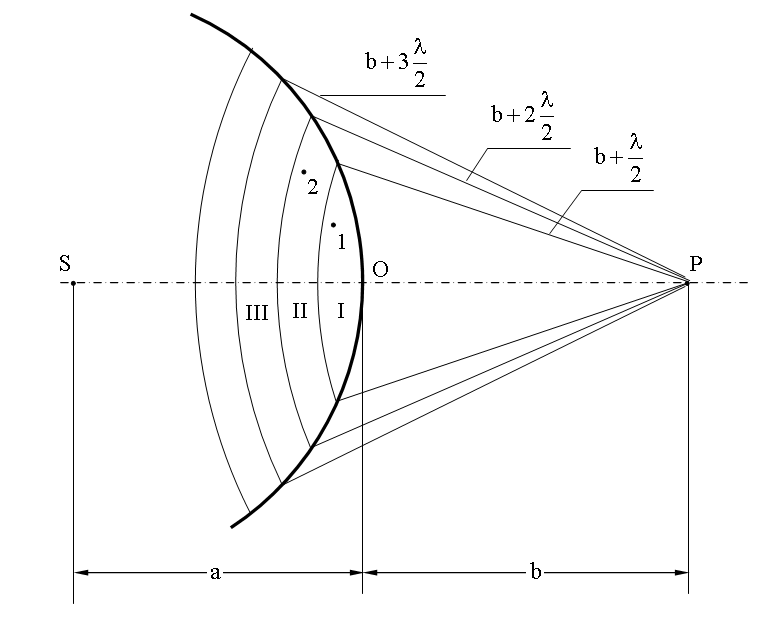
Из геометрических соображениях следует, что при не очень больших номерах зон их площади примерно одинаковы. Значит каждой точке первой зоны найдется соответствующая ей точка во второй, колебания которых погасят друг друга. Амплитуда результирующего колебания, приходящего в точку P от зоны с номером m, уменьшается с ростом m, т.е.

37. Дифракция на круглом отверстии. Сферическая волна, распространяющаяся из точечного источника S, встречает на своем пути экран с круглым отверстием. Дифракционную картину наблюдаем на экране Э в точке В, лежащей на линии, соединяющей S с центром отверстия (рис. 259). Экран параллелен плоскости отверстия и находится от него на расстоянии b. Разобьем открытую часть волновой поверхности Ф на зоны Френеля. Вид дифракционной картины зависит от числа зон Френеля, открываемых отверстием. Амплитуда результирующего колебания, возбуждаемого в точке В всеми зонами (см. (177.1) и (177.6)),

где знак плюс соответствует нечетным m и минус — четным т.

Когда отверстие открывает нечетное число зон Френеля, то амплитуда (интенсив­ность) в точке В будет больше, чем при свободном распространении волны; если четное, то амплитуда (интенсивность) будет равна нулю. Если отверстие открывает одну зону Френеля, то в точке В амплитуда А=А₁, т. е. вдвое больше, чем в отсутствие непрозрачного экрана с отверстием. Интенсивность света больше соответственно в четыре раза. Если отверстие открывает две зоны Френеля, то их действия в точке В практически уничтожат друг друга из-за интерференции. Таким образом, дифракционная картина от круглого отверстия вблизи точки В будет иметь вид чередующихся темных и светлых колец с центрами в точке В (если т четное, то в центре будет темное кольцо, если m нечетное — то светлое кольцо), причем интенсивность в максимумах убывает с расстоянием от центра картины.

Расчет амплитуды результирующего колебания на внеосевых участках экрана более сложен, так как соответствующие им зоны Френеля частично перекрываются непроз­рачным экраном. Если отверстие освещается не монохроматическим, а белым светом, то кольца окрашены.

Число зон Френеля, открываемых отверстием, зависит от его диаметра. Если он большой, то А_m<<A₁ и результирующая амплитуда A=A₁/2, т. е. такая же, как и при полностью открытом волновом фронте. Никакой дифракционной картины не наблю­дается, свет распространяется, как и в отсутствие круглого отверстия, прямолинейно.