5. За рисунком 3 знайти х

А	Б	В	Г	Д
77	70	72	80	60

6. На рисунку 4 ОS перпендикулярно до АС. SА = 15 см. Знайти СА.

А	Б	В	Г	Д
15 см	20 см	45 см	30 см	Неможливо визначити

7. Діагональ трапеції поділяє її середню лінію на відрізки 7см і 10 см. Знайти основи трапеції.

А	Б	В	Г	Д
5 см і 20 см	7 см і 30 см	21 см і 30 см	Визначити неможливо	14 см і 20 см

8. Знайти у прямокутному трикутнику, з гострим кутом 30⁰ і меншим катетом 21 см, відрізки, на які медіана, проведена до гіпотенузи, поділяється іншою медіаною.

А	Б	В	Г	Д
15 см і 12 см	7 см і 14 см	8 см і 16 см	5 см і 9 см	6 см і 24 см

Частина 2

Завдання 9 передбачає установлення відповідності між відношеннями (1 – 4) та їх значеннями (А – Д).

9. В трикутнику MNL проведені медіани NP i MK, що перетинаються в точці A. Промінь AT перетинає сторону NL в точці T так, що ML //AT Знайти відношення відрізків (1 - 4) і відповіді обрати серед варіантів А – Д.

1	MA : AK		A	2 : 1
2	NK : TK		Б	3 : 1
3	NT : NL		В	1 : 2
4	NP : AP		Г	2 : 3
			Д	3 : 1

Частина 3

Завдання 10 -11 відкритої форми з короткою відповіддю.

Розв’яжіть завдання та запишіть відповіді.

10. Бісектриса кута А трикутника АВС перетинає сторону ВС в точці М. З точки М проведена пряма паралельна стороні АВ, що перетинає АС в точці К. Знайти відрізки АК і КС, якщо АВ = 12, АС = 20.

11. В трикутнику РМК до сторони РК проведені паралельні прямі ВS і OQ (B i O належать РМ, S і Q – МК) так, що ВМ = 9 см, ВО = 11 см, МQ = 40 см. Знайти МS.

Частина 4

Завдання 12 -13 відкритої форми з розгорнутою відповіддю.

Розв’яжіть завдання та запишіть відповіді.

12. Катети прямокутного трикутника рівні 6 см і 8 см. Півколо, центр якого лежить на гіпотенузі, дотикається катетів. У якому відношенні центр кола поділяє гіпотенузу.

13. У паралелограмі АВСD точки F і E – середини сторін AВ і CD відповідно. Відрізок CF перетинає діагональ BD в точці S, а відрізок AE – в точці K. Знайти відношення

ВO : ОК, якщо О – точка перетину діагоналей.

Відповіді

№	В – 1	В – 2	В – 3	В – 4
1	Б	Д	Г	Б
2	Г	В	Б	А
3	Д	Г	В	В
4	А	В	Д	Б
5	Д	А	А	Г
6	В	Б	А	Г
7	А	Г	Б	Д
8	Б	Д	Г	Б
9	1 - В 2 - А 3 - Д 4 - Г	1 - А 2 - В 3 - Б 4 - Д	1 - Б 2 - Д 3 - Г 4 - А	1 - А 2 - Д 3 - Г 4 - Б
10	8 см	4,8 см, 3,2 см	10 см	12,5; 7,5
11		10 cм або 160 см		18
12	2 : 3	20 : 21	3 : 4	4 : 3
13	1 : 2	1 : 6	1 : 4	3 : 1

Частина третя

10.

Н ехай АВС заданий трикутник, висота якого ВD = 20, АВ = ВС, точка О – центр вписаного кола, радіус якого ОD. Оскільки центр вписаного кола лежить на перетині бісектрис, то АО – бісектриса трикутника АВD. АВ :

АD = 3 : 2 за умовою задачі. Позначимо ОD – х, тоді ВО – (20 - х). За властивістю бісектриси трикутника маємо рівняння:

;

Відповідь: 8 см.

11.

ABCD – даний паралелограм. AN = ND, BM = MC. Чотирикутник BMDN – паралелограм за ознакою

(BM // ND, BM = ND), тому КО = ОЕ. Розглянемо кут ВСА: за теоремою Фалеса КЕ : ЕС = ВМ : МС = 1 : 1. Аналогічно, АК = КЕ (кут САD).

Отже, АК : КС = 1 : 2

В – 2

Частина перша

1	2	3	4	5	6	7	8
Д	В	Г	В	А	Б	Г	Д

Частина друга

	А	Б	В	Г	Д
1
2
3
4

Частина третя

10. - заданий. За властивістю бісектриси кута А

Розглянемо кут С: за теоремою Фалеса

Позначимо АК – х, тоді КС – (8 – х). Маємо рівняння:

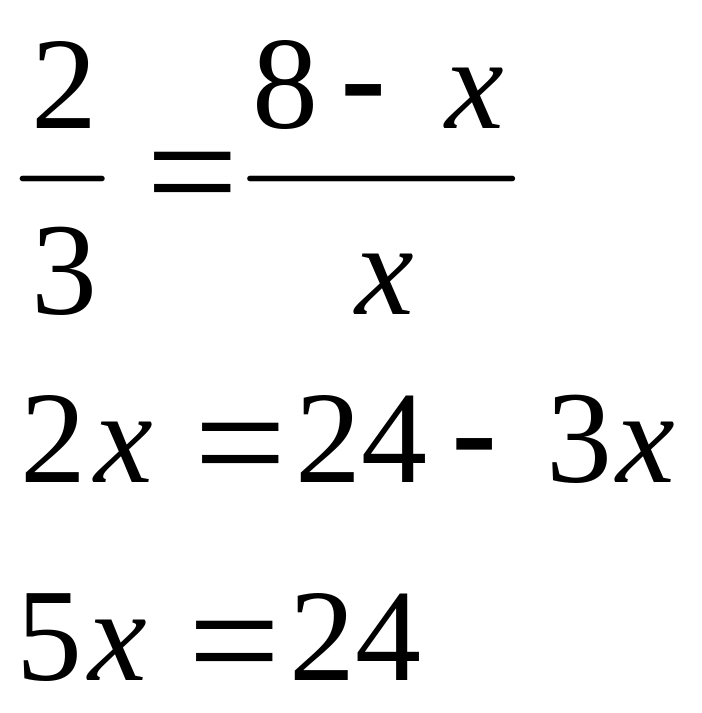
Отже, АК = 4,8; КС = 8 – 4,8 = 3,2.

11. В ідповідь:

В – 3 В - 4

	А	Б	В	Г	Д
1
2
3
4

	А	Б	В	Г	Д
1
2
3
4