МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ

Донецкий национальный технический университет

Кафедра геоинформатики и геодезии

Методические указания

к лабораторным работам по курсу «Высшая геодезия»

Раздел: «Теоретическая геодезия»

для студентов специальности: 7.070901 «Геодезия»

7.070904 «Землеустройство и кадастр»

7.070908 «Геоинформационные системы

и технологии»

Рассмотрено

на заседании кафедры

геоинформатики и геодезии

Протокол № ___ от ___________

Донецк ДонНТУ – 2010

УДК 528.28

Методические указания к лабораторным работам по курсу «Высшая геодезия» (раздел –Теоретическая геодезия) (для студентов специальности 7.070901 «Геодезия», 7.070904 «Землеустройство и кадастр», 7.070908 «Геоинформационные системы и технологии») / Сост.:Ю.Н.Гавриленко, Е.О.Маланчук. – Донецк; ДонНТУ. 2010. – 27 с.

Содержит рекомендации, практические примеры решения типовых задач, относящихся к вопросам теоретической геодезии: определение уклонений отвесных линий и высот квазигеоида, системы высот, редуцирование измерений на поверхность эллипсоида.

Составители: профессор Ю.Н.Гавриленко

ассистент Е.О.Маланчук

Отв.за выпуск: профессор С.Г.Могильный

Рецензент: профессор А.А.Шоломицкий

Лабораторная работа №1 Вычисление уклонений отвесных линий и высоты квазигеоида методом численного интегрирования по гравиметрической карте

Уклонения отвесных линий и высота квазигеоида определяются по формулам Венинг-Мейнеса и Стокса:

(1.1)

(1.2)

, (1.3)

где: – аномалия силы тяжести;

– функция Венинг-Мейнеса

– функция Стокса.

Непосредственное решение поставленной задачи оказывается практически невозможным, поэтому применяют графическое решение.

При наличии карты аномалий прилегающую к определяемой точке местность разбивают рядом концентрических окружностей и радиусов на участки равного влияния аномалий на уклонения отвеса. Учет влияния всего пространства сводится в этом случае к суммированию средних аномалий всех участков и умножению суммы на постоянное число – влияние аномалии в 1 мГал.

Разбиение окружающего пространства на области равного влияния осуществляют при помощи палетки В.Ф.Еремеева.

Построение палетки в.Ф.Еремеева.

Палетка строится на кальке размером 2525 см. В центре листа намечают точку и проводят линию S-N. От этого направления под углом 1115′ в обе стороны проводятся радиусы (рис.1.1). Полученный сектор включает в себя направление S-N и имеет номер 16. Затем от него строится еще 15 секторов с центральным углом 2230′. Секторы нумеруют арабскими цифрами, считая вправо от первого радиуса.

Далее строят кольцевые зоны. Их нумеруют римскими цифрами от І до VIII. Размеры кольцевых зон приведены в табл.1.1.

Таблица 1.1 – Размеры круговых зон в палетке В.Ф.Еремеева
Номер зоны	0	I	II	III	IV	V	VI	VII	VIII
Размер зоны, км	0 –5,0	5,0 – 7,3	7,3 –10,7	10,7–15.7	15,7–22,8	22,3–33,3	33,3–48,5	48,5–70,6	70,6–102,6

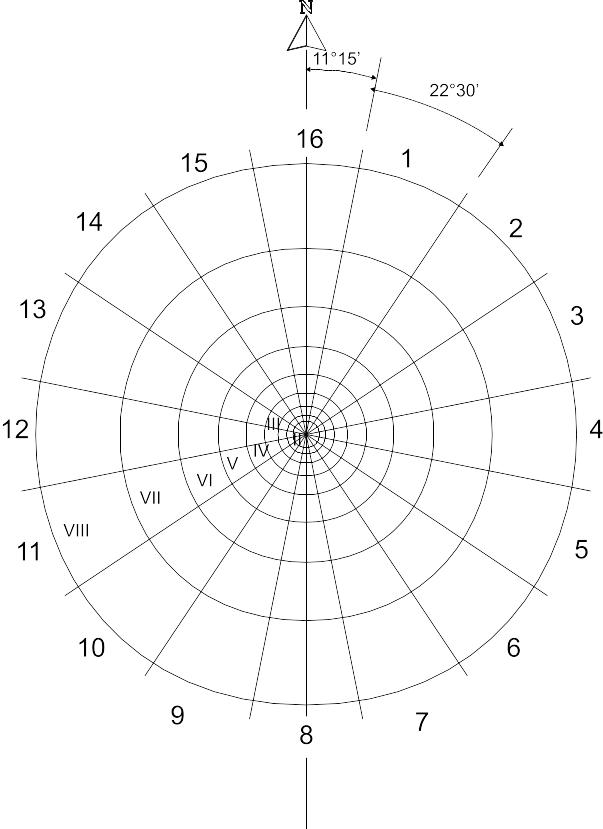
Рисунок 1.1

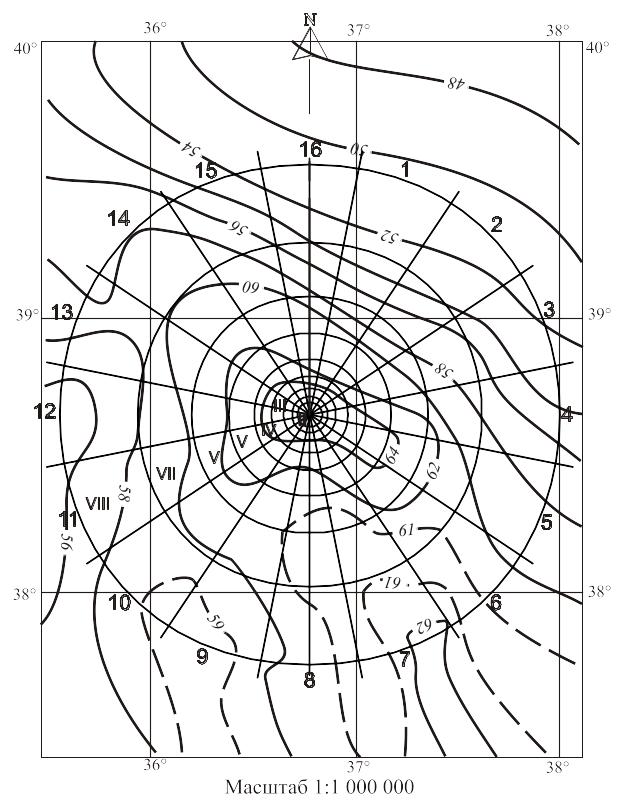
Таким образом, получена центральная зона под номером 0 и радиусом 5 км и ближние зоны в виде криволинейных трапеций с адресом: номер зоны - номер сектора, например, II-12. На рис.2.1 показана палетка, совмещенная с гравиметрической картой.

Рисунок 1.2 – Фрагмент гравиметрической карты с палеткой