Из Лекций.

Затухающий импульс можно получить от 2х колебательных контуров включенных встречно.

Схема: от сети заряжаются конденсаторы- 1 полупериод С2 через R3, 2 полупериод С1; Ток проходит через индуктивности контуров включенных встречно; когда сработает разрядник-потечет ток- высокое испытательное напряжение.

Вместо L2 можно использовать R2, тогда Uс2 будет падать по экспоненте( см. график ниже).

4. Определить пробивное напряжение конденсатора с газообразным диэлектриком, если известны его электрическая емкость С, площадь электродов S_П и электрическая прочность газа Е_Р (табл. 4). Напряжение к обкладкам конденсатора прикладывается "толчком" и выдерживается длительное время.

Определить предразрядные времена t_H , t_З , при которых пробои газового диэлектрика соответственно начинаются и заканчиваются при воздействии на конденсатор импульсов напряжения различной формы:

U = U_Мsin^1/4ωt ; ;

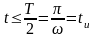U = U_Мsin^1/2ωt ;

U = U_Мsinωt ;

U = U_Мsin²ωt .

При расчетах амплитуда импульса определяется выражением U_м = aU_р , где U_р – величина разрядного напряжения; a – постоянный коэффициент. Частота электрического напряжения составляет 50 Гц.

Провести физический анализ полученных результатов и установить область их практического использования.

Таблица 4. Варианты домашнего задания по разделу 4.1 (задача 4)
№ варианта	С, пФ	SП, см2	ЕP, кВ/мм	а
1	30	400	2,7	1,5
2	40	500	2,8	2,0
3	50	600	2,9	2,5
4	60	700	3,0	3,0
5	70	800	3,1	3,5
6	80	900	3,2	1,7
7	90	450	3,3	1,9
8	100	550	3,4	2,1
9	35	650	3,5	2,3
10	45	750	3,6	2,6
11	55	850	2,7	2.7
12	65	430	2,8	2,9
13	75	530	2,9	3,1
14	85	630	3,0	3,3
1В	95	730	3,1	3,4
1в	32	830	3,2	1,3
17	42	930	3,3	2,4
18	52	460	3,4	2,9
19	62	560	3,5	3,7
20	72	670	3,6	4,3
21	82	780	2,8	4,1
22	92	810	3,1	3,9
23	46	935	2,9	2,8
24	56	867	3,2	2,4
25	77	578	3,4	1,7

2. Рассчитать и построить зависимости P(1,U_M) в области малых вероятностей появления случайной величины 0,001 < P(1,U_M) < 0,1 для двух типов зависимостей P(1,U_M): интегральных кривых нормального закона распределения и трехпараметрического распределения Гнеденко-Вейбулла. При этом параметры распределений для функций P(1,U_M) взять из предыдущей задачи (табл. 6). Расчетные данные представить в виде таблицы, в которой также привести расчетные данные по степени расхождения значений P(1,U_M) при заданном U_M во всей области малых вероятностей P(1,U_M), которую рассчитать по формуле

где P_Н(1, U_М) , P_В(1, U_М) – зависимости при нормальном и трехпараметрическом распределениях.

Оценить области наибольшего расхождения значений вероятностей и сформулировать предложения к оптимальному выбору зависимости P(1, U_М), которую можно было бы использовать для практических расчетов, в том числе и при перерасчете результатов испытаний с малых образцов на большие.

Экзаменационный билет №5