15) Рассмотрите обобщенное отображение пекаря. Проиллюстрируйте возникновение странного хаотического аттрактора

Допустим, что разрез имеет различное соотношение, но α + β = 1. О ба куска растягиваются по горизонтали до единичной длины, сжимаются по вертикали, так что их высоты будут соответственно μ и ν, μ + ν < 1, и располагаются в пределах единичного квадрата у верхнего и нижнего его края. Тогда для x ≤ α , x > α . Система диссипативна и имеет двумерное фазовое пространство, так как сумма μ + ν < 1. С каждой новой итерацией, площадь будет уменьшаться. Образуется характерная система горизонтальных полос, суммарная ширина которых убывает с ростом числа итераций как ( )ⁿ . Объект, возникающий в пределе бесконечно большого числа итераций, в сечении представляет собой, так называемое двухмасштабное канторово множество. Берется единичный отрезок, делится в отношении

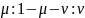, и средняя часть исключается. То же проделывается с двумя оставшимися отрезками, затем с каждым из отрезков, возникших на предыдущем шаге. Классическое множество отвечает частному случаю.

Аттрактор имеет нулевую меру, поскольку суммарная площадь полос на n-м шаге дается выражением (μ + ν)ⁿ и стремится к нулю при n , так как μ + ν < 1. Все точки исходного единичного квадрата приближаются к аттрактору. В тоже время аттрактор обладает тем свойством, что соседние по горизонтали точки удаляются друг от друга при последовательных итерациях, т.е. имеет место неустойчивость. Обобщенное отображение пекаря не является непрерывным.

16 Рассмотрите задачу об одномодовом лазере.

Уравнения динамики одномодового лазера

Еще одна, совершенно иная физическая система, которая опи­сывается уравнениями Лоренца, — это модель одномодового лазера (Ораевский, 1981, 1996).

Предположим, что имеется резонатор (рис. 3.5), в котором мо­жет возбуждаться одна мода — колебания электромагнитного поля на определенной частотеω₀ и с фиксированной пространственной

структурой. Амплитуда колебаний может медленно изменяться во времени благодаря присутствию потерь и взаимодействию поля с активной средой, заполняющей резонатор. Активная среда со­стоит из атомов с двумя энергетическими уровнями, причем раз­ность энергий между уровнями ΔЕ=hω₀, где h — постоянная Планка. Иными словами, частота перехода считается точно совпадающей с собственной частотой моды резонатора, расстройка отсутствует. Далее, предполагается, что присутствует механизм накачки, благодаря которому атомы переходят с нижнего уровня на верхний и в среде создается, как говорят, инверсная заселен­ность. Как будут выглядеть уравнения, описывающие динамику такой модели?

Выясним сначала, с какими динамическими переменными нам предстоит работать. Электрическое поле в резонаторе представим в виде

гдеE(t) — медленно меняющаяся амплитуда, E_s(r) характеризует распределение в пространстве поля рабочей моды резонатора. Да­лее, естественно предположить, что вектор поляризации активнойсреды — дипольный момент единицы объема характеризуется та­ким же пространственным распределением, как и электрическое поле, и может быть представлен в виде

Наконец, введем величину, характеризующую мгновенную раз­ность населенностей уровней, — инверсию

где N₁ и N₂ — число атомов, пребывающих в данный момент, со­ответственно, на нижнем и верхнем энергетическом уровне. Итак, мы должны сконструировать уравнения, описывающие динамику во времени величин Е, Р иD.

Выпишем сначала уравнение возбуждения резонатора. В ле­вой части будет стоять производная от амплитуды поля , а в правой — член, пропорциональный поляризации Р, отвечающий за возбуждение поля атомами среды, и член, описывающий потери энергии колебаний моды:

где α — параметр потерь, β — некоторая постоянная.

Второе уравнение, имеющее в левой части производную 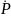, описывает изменение поляризации активной среды. В правой ча­сти будет присутствовать релаксационный член (-γР) и еще один член, происхождение которого можно пояснить следующим обра­зом. Дипольный момент, который приобретает каждый атом ак­тивной среды в присутствии электрического поля, пропорциона­лен величине поля и зависит от того, на каком энергетическом уровне находится атом. Поэтому средний вклад в поляризацию будет пропорционален произведению амплитуды поля и разности населенностей. Таким образом, второе уравнение имеет вид

где γ и с — постоянные.

Наконец, третье уравнение описывает изменение инверсии на­селенностей и имеет вид

где Г — параметр релаксации населенностей, aD₀ характеризует интенсивность накачки. Член вида ЕР соответствует мощности, которую тратит поле на поляризацию среды (эта мощность может быть положительной или отрицательной). Если энергия переда­ется полю, инверсия уменьшается.

Заменой переменных и параметров

уравнения (3.32)-(3.34) приводятся к виду

Эти соотношения превращаются в уравнения Лоренца, если по­ложитьω = r-z. Таким образом, в лазерной интерпретации переменнаяxотвечает амплитуде поля,y— поляризации, az— инверсии населенностей. Место параметра геометрии bи числа Прандтля σ занимают отношения коэффициентов релаксации ин­версии и поля к коэффициенту релаксации поляризации. Интен­сивность накачки играет ту роль, какую в гидродинамической си­стеме играло число Рэлея.