7.Дайте определение бифуркационной диаграмме. На качественном уровне рассмотрите бифуркационную диаграмму логистического отображения.

Широко используемым способом исследования предхаотических или послехаотических изменений динамической системы при вариации ее параметров является построение бифуркационных диаграмм.

Под бифуркационной диаграммой подразумевают изображение на рисунке смены возможных динамических режимов системы (равновесных состояний, стационарных точек, периодических орбит и пр.) при изменении значения бифуркационного параметра. Одной из простейших задач является модель роста популяции, или логистическое уравнение

, . (1)

где х_n – реализация физической величины, r– управляющий параметр.

Бифуркационная диаграмма логистического отображения приведена на рис. 3.1.

Рис. 3.1. Бифуркационная диаграмма логистического отображения

На рисунке хорошо видны точки бифуркаций удвоений периода, где каждая ветвь дерева расщепляется на две. Когда параметр системы становится больше критического значения, в определенных диапазонах значений параметра движение становится хаотическим, соответствующие области выглядят как более или менее равномерно заполненные точками участки "кроны". Однако такие диапазоны могут иметь конечную ширину; другими словами, при изменении параметра могут встречаться окна периодического движения. В этом режиме периодические движения могут вновь проходить через бифуркации удвоения периода, вновь приводя к хаотическому движению.

8 .Приведите основные этапы построения карты динамических режимов автоколебательной системы.

Представленные выше иллюстрации относились к случаю, когда изменялся один параметр системы. Поведение систем, зависящих от двух (и более) параметров оказывается значительно более сложным. Для анализа таких нелинейных систем существует простой компьютерный метод, который основан на численном определении типа режима. Результат представляется на плоскости параметров, на которой каждая точка окрашена в соответствующий цвет. Например, режим периода 1 - зеленым, периода 2 – желтым, периода 4 – синим и т.д., а серым цветом – области хаоса. Такой анализ выявляет некоторые типичные структуры, а также области тонкой и сложного устройства плоскости параметров. Для исследователя он является своего рода «географической картой», дающий представление о типах режимов при «путешествии» по разным маршрутам.      На рисунке показана карта режимов для отображения Икеды  , которое описывает динамику возбуждаемого внешними импульсами нелинейного осциллятора.

     Аналогичные карты можно построить для других нелинейных систем.

9 .Рассмотрите на качественном уровне фазовый портрет системы Лоренца

   Рассмотрим поведение системы Лоренца

 

Рисунок 1 уравнение(13.1) Система Лоренца

при   и         При   седловые предельные циклы L₁ и L₂ стягиваются соответственно к стационарным точкам O₁ и O₂ и при r = r₃ исчезают, сливаясь с ними; стационарные точки O₁ и O₂ становятся при этом неустойчивыми. 

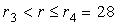     При   все стационарные точки (O, O₁ и O₂) являются неустойчивыми. Единственным устойчивым предельным множеством - аттрактором - будет B₂, т. е. аттрактор Лоренца (см. рисунок). Следовательно, в системе (13.1) при любых начальных условиях будет устанавливаться хаотический режим движения. Хаотическая траектория аттрактора, представленного на рисунке (внизу), просчитывалась при   и начальных условиях   плоскость (x, y) соответствуетz = 27. 
     Таким образом, можно сделать вывод, что диссипативные динамические системы (например, система Лоренца), размерность фазового пространства которых больше или равна трём, могут иметь наряду с регулярными и очень сложные, хаотические режимы движения. Математическим представлением такого хаотического поведения диссипативных систем является притягивающее множество сложной структуры - странный аттрактор.