1.Сформулируйте основные понятия динамических систем. Проведите историческое введение в теорию динамического хаоса.Динамические системы - это системы, которые под действием внешних и внутренних сил изменяют во времени свои состояния. Представления о динамических системах возникли как обобщение понятия механической системы, поведение которой описывается законами динамики. В современной науке понятие динамической системы охватывает системы практически любой природы—физические, химические, биологические, экономические, социальные и др. При этом системы характеризуются различной внутренней организацией—жестко-детерминированные, стохастические, нелинейные, системы с элементами самоорганизации, самоорганизующиеся. Важнейшим свойством динамических систем является их устойчивость, т. е. сохранение системой своей базовой структуры и основных выполняемых функций в течение определенного времени и при относительно небольших и разнообразных внешних воздействиях и внутренних возмущениях. Устойчивость есть внутреннее свойство систем, а не результат внешнего воздействия. Представления же о развитии этих систем отражают такие изменения их структурной организации, которые ведут к более эффективному выполнению системой своих основных функций. Качественные перестройки систем анализируются в теории катастроф, которая рассматривается как ветвь общей теории динамических систем.Историческое введние.1.Механика. Ньютон, Лаплас, Лагранж, Гамильтон – результат их деятельности стало формирование представления о том, что мы сейчас называем консервативной или гамильтоновой системой. Проблема трёх тел в небесной механике – первая задача, анализируя которую исследователи столкнулись с возникновением сложной динамики и хаоса. Новым толчком к развитию исследований стало появление компьютеров и вычислительных машин. Одним из первых примеров компьютерного исследования стала работа французских астрофизиков М. Хенон и С. Хейлис, рассмотревших модель движения звезды через галактический диск. Значительный прогресс в понимании соотношения между квазипериодической динамикой и хаосом связан с теорией, которую создали в 50-60-х годах А.Н. Колмагоров, В.И.Арнольд и Ю. Мозер (теория КАМ). Основная теорема утверждает, что при включении достаточно слабого взаимодействия между движениями нелинейных систем с иррациональным соотношением частот квазипериодический характер динамики в большинстве случаев сохраняется.

2.Статическая физика. Гиббс (1839-1903), Больцман(1844-1906) – рассматривали фазовое пространство гамильтоновых систем, образованных совокупностью большого числа микрочастиц. Работы Ляпунова (1857-1918) показали количественную характеристику неустойчивости систем. Энтропия Калмагорова-Синая (1959) позволяет определить простую или сложную динамику системы.

3.Теория колебаний, радиофизика и электроника. Б.Ван-дер-Поль (1889-1959) – создание классической модели – периодического нелинейного осциллятора, который носит его имя. Режим работы устройства контролировался с помощью звука в наушниках. Исследователи отметили явление синхронизации при определённых соотношениях частот генератора и внешнего воздействия.

В России в 20-е годы в Московском университете сформировалась школа Мандельштама. В к. 20-х годов ученика Мандельштама Андронов установил, что адекватным математическим образом периодических автоколебаний являются предельные циклы. Одно из важных достижений – исследование момента возникновения автоколебаний при изменении параметров, ситуации, которую теперь называют бифуркацией Андронова – Хопфа. Также важным достижением стало формирование Андроновым и Понтрягиным представление о грубых или структурно-устойчивых системах.

4.Гидродинамика. Теория турбулентностей. Число Рейнольдса (1842-1912), которое показывает, будет ли течение жидкости турбулентным или ламинарным. Работы Ландау (1908-1968) и Хопфа (1902-1983) по возникновению турбулентности в результате бифуркаций называют сценарием Ландау-Хопфа. В 1963 году Лоренц показал, что динамику жидкости можно описать через три дифференциальных уравнения (конвекция жидкости подогреванием снизу), показал связь между сложной динамикой и неустойчивостью фазовых траекторий (эффект бабочки).

5.Дискретное отображение. Т. Мальтус (1766-1834) – автор концепции о том, что численность человечества растёт в геометрической а средства поддержания жизни – в арифметической прогрессии, поэтому численность людей должна регулироваться войнами, болезнями и т.д. Вводится логистическое отображение .

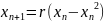В 1975 году Ли и Йорк публикуют работу «Период 3 означает хаос». Если при каком-то значении R отображение имеет цикл периода 3, то оно имеет бесконечное множество циклов всех прочих периодов.

В 1978-1979 году Фейгенбаум разрабатывает теорию универсального удвоения периода.

6.Математика. Разработка теории бесконечных множеств Г. Кантором (1845-1918). Введение множеств с нецелой размерностью Хаусдорфа (1868-1942) называют фракталами. Понятие фрактал ввёл Мандельброд в своей книге «Фрактальная геометрия».

7.Прикладной хаос. Работы Болта и Ме йса (1995) где рассматривается применение методики управления хаосом для отправления объекта на Луну. Разработка методики по обработке сигналов, их качественного анализа для выявления природы и структуры источника сигнала. Конструирование моделей управления хаосом применительно к медицине и биологии. В телекоммуникации – защита информации хаосом, новые методики кодирования инфомрации.

2.Объясните различия между линейным и нелинейным уравнениями колебаний математического маятника.

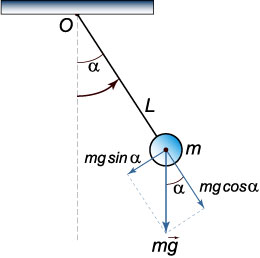
Математический маятник представляет собой идеальную модель, в которой материальная точка массой m подвешена на невесомой и нерастяжимой нити длиной L. В такой системе происходят периодические колебания, которые можно рассматривать как вращение маятника вокруг оси O (рисунок 1).

Рис.1		Рис.2

Динамика вращательного движения описывается дифференциальным уравнением

где ε − угловое ускорение, M − момент силы, вызывающий вращение, I − момент инерции тела относительно оси вращения.  В нашем случае момент силы определяется проекцией силы тяжести на тангенциальное направление, т.е.

Знак минус означает, что при положительном угле поворота α (против часовой стрелки) момент сил вызывает вращение в противоположном направлении.  Момент инерции маятника выражается формулой

Тогда уравнение динамики принимает вид:

В случае малых колебаний полагают sin α ≈ α. В результате возникает линейное дифференциальное уравнение

где 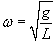  − круговая частота колебаний.  Период малых колебаний маятника описывается известной формулой

Однако при увеличении амплитуды колебаний линейная формула перестает быть справедливой. В этом случае для корректного описания колебательной системы нужно решать исходное нелинейное дифференциальное уравнение.

3.Опишите классический пример автоколебательной системы – генератор Ван-дер-Поля

Осциллятор Ван дер Поля — осциллятор с нелинейным затуханием.

Система Ван-дер-Поля – является «эталонной» моделью теории колебаний и нелинейной динамики, описывающую автоколебания и простейший вариант бифуркации Андронова-Хопфа. При наличии внешнего гармонического воздействия.

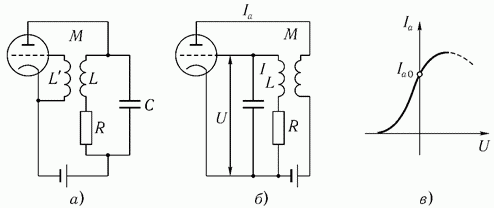
Схемы генераторов Ван-дер-Поля: а — с контуром в цепи анода; б - с контуром в цепи сетки; в — характеристика лампы, аппроксимированная кубическим полиномом

Вынужденные колебания.

Вынужденные колебания осциллятора Ван дер Поля как с потерями энергии, так и без иных рассчитываются по формуле

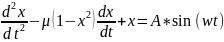
где

A — амплитуда внешнего гармонического сигнала,

w — его угловая частота.

x - координата точки зависящая от времени

µ - некий коэффициент, характеризующий нелинейность и силу затухания колебаний

У осциллятора Ван дер Поля существуют два режима: при µ = 0 и при µ>0. Очевидно, что третьего режима µ<0 — не существует, так как трение в системе не может быть отрицательным.

1) Когда µ = 0 , то есть осциллятор рассчитывается без затухания

Это уравнение гармонического осциллятора.

2) При µ>0 система имеет некие предельные циклы. Чем дальше µ от нуля, тем хаотичнее ведёт себя система.

4.Дайте понятие фазового портрета динамической системы.

Фазовый портрет- совокупность фазовых траекторий, характеризующая состояния и  движения динамической системы.

Поведение динамической системы изучают в "пространстве состояний". Точка в этом пространстве однозначно задает состояние системы в простейшем случае, например, для маятника - это плоскость (координата, скорость). Притягивающие объекты в фазовом пространстве - аттракторы - определяющие свойства установившегося с течением времени колебательного процесса в системе. Аттрактор (от английского to attract - притягивать) может иметь вид простой замкнутой кривой. это предельный цикл являющийся образом автоколебаний.

Подход основанный на таких представлениях, явился революционным в нелинейной теории, поскольку позволил сопоставить эволюции системы во времени наглядные геометрические образы. В настоящее время построение фазового портрета на компьютере - атрибут почти любого исследования. Экспериментаторы получают фазовые портреты на экране осцилографа.

Для качественного исследования динамической системы большое значение имеет зависимость решения системы ОДУ от начальных условий. Очень наглядным образом можно визуализировать такую информацию на фазовой плоскости. Каждое решение будет выходить из точки, координаты которой являются начальными условиями. Множество решений, вычисленное для всевозможных начальных условий, образует фазовый портрет динамической системы. С вычислительной точки зрения задача исследования фазового портрета часто сводится к обычно мусканированию семейств решений ОДУ при разных начальных условий (например, при помощи алгоритма Рунге-Кутты).  В частности, фазовый портрет системы модели динамики популяций(Вольтерра), определенный для нескольких (четырех) начальных условий,  изображен на рис.