1. Биномдық үлестіру бойынша ненің ықтималдығын табуға болады.Физикада биномдық үлесуді қайда қолданады.Биномдық үлестірулер — тәуелсіз сынаулар тізбегіне байланысты болып келген негізгі ықтималдықтар үлестірілулерінің бірі. А оқиғасының P ықтималдығы деп А-ға қолайлы элементар оқиғалар санының барлық мүмкін оқиғалар санына қатынасын айтады.Классикалық жағдайда тәжірбие саны тең ықтималды элементар оқиғалардың шекті санынан құралады. Тиынның “елтаңба” жағымен түсу ықтималдығы 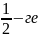тең екендініне қалай көз жеткізуге болады? Ол үшін n тәжірбие нәтежиесінде 50% елтаңба, 50% сан жағы түсу керек.Практикада егер n саны аз болса бұл жүзеге аспауы мүмкін.Мысалы 10 рет лақтырылғанда“елтаңба” жағы 5 рет , сан жағы 5 рет болмауы әбден мүмкін.Бірақ тәжірбие саны n өскен сайын тең ықтимал заңдылығы дәлірек орындалады: 100 сынақта 10-қарағандa дәлірек,1000 сынақта одан да дәлірек.Сонымен сынақ n рет жүргізілсін.Осы кезде А оқиғасының k рет болуы биномдық үлесу заңына бағынады.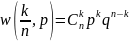 . Мұнда 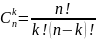-n-нен k бойынша теру , p – “елтаңбаның” жеке бір рет лақтырғанда түсу ықтималдығы (немесе А оқиғасының ықтималдығы ), q- “елтаңбаның” жеке бір рет лақтырғанда түспеу ықтималдығы( немесе жеке бір сынақта А оқиғасының болмай B оқиғасының - тиынның сан жағымен түсу ықтималдығы).

Биномдық үлесу төменгі шарттар үшін орындалады:

• Сынақ саны n тұрақты

• Әрбір сынақ нәтежиесі басқа сынақ нәтежиелеріне тәуелсіз

• А оқиғасының болу ықтималдығы сынақ номеріне тәуелді емес(p=const)

• А оқиғасының болмау ықтималдығы q=1-p

Аталған шарттар жиынтығы биномдық эксперименттердің математикалық моделі деп аталады.

Биномдық үлесуді молекулалық физикада қолдану.Макрокүй ықтимадығы . Макрокүй саны өте көп микрокүйлер арқылы жүзеге асады.Егер осы микрокүйдің барлық белгілері мәлім болса,онда осы белгілерге сәйкес келетін барлық макрокүйлерді көрсетуге және олардың санын санауға болады.Айталық 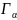микрокүйлер саны,ал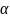 макрокүйді сипаттасын , 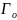барлық микрокүйлер саны болсын.Онда микрокүйлердің тең ықтималдығы туралы постулат негізінде қарастырып отырған макрокүй ықтималдығы: w( )= .

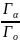Лаплас Гаусс және Гаусс таралуларының биномдық үлесуден айырмашылығы. Л.Г. Ықтималдық үлесуінің биномдық заңы n шексіздікке жағдайында Лаплас Гаусс өрнегін береді.Факториалдарға Стирлинг өрнегін қолданып

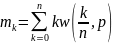өрнегін төмендегідей жазуға болады:

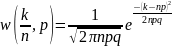(1) .Осыны Лаплас-Гаусс өрнегі деп атайды.Осы үлесу биномдық үлесуге сәйкес келетінін ескерсек онда Л.Г. үлесуінің математикалық күтімі мен дисперсиясы 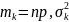=npq бойынша есептеледі.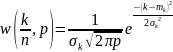 .(2) Демек n үлкен болған жағдайда . орнына (1),(2) өрнектерін қолдануға болады.Бұл жерде к кездейсоқ шамасы биномдық заңдағыдай дискретті шама болып табылады.

Г. Бұл үлестіру өлшенетін физикалық шаманың мәні кездейсоқ шама екекін жете түсіну эксперимент нәтежиесін өңдеу үшін ықтималдық теориясын қолдануға мүмкіндік береді.Механика бөліміндегі 1лаб.қ жұмыста электр импульстарын өлшеу нәтежиелері Гаусс үлесуіне сай келетін 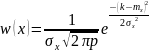.Мұнда 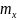x шамасының математикалық күтімі, 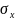дисперсия. Өлшенген x шаманың x, x+dx интервалында болу ықтималдығы w(x) функциясымен анықталады.(аталған ықтималдық w(x)dx-ке тең.)

“

Өлшеуіш құрал – «зерттелуші объект» жүйесіне n кездейсоқ бақылануы мүмкін емес себептер әсер етеді.Олардың әрқайсысы бір біріне тәуелсіз және 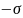ауытқу тудырады және де 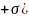p( +p(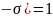 .Осы ауытқулар жиынтығы физикалық шама мәнінің 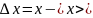қателігіне алып келеді.

Осы модель терминдерінің атауына дейінгі дәлдікпен биномдық эксперимент моделіне сәйкес келеді,ал Л.Г. үлесуі практика жүзінде Г. Заңына сәйкес.Осы өрнектер арасындағы айырмашылық біреу,ол үлесуде кездейсоқ шама к дискретті шама болса,үлесудегі аргумент х үздіксіз кездейсоқ шама. Үздіксіз кездейсоқ х шамасының негізгі сипаттамалары математикалық күтімі мен дисперсиясы төменгі өрнектермен анықталады: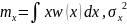 = 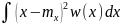. Гаусс үлесуін қолдана отырып идеал газ молекулаларының жылдамдық пен кинетикалық энергия бойынша үлесуін Максвел үлесуін алуға болады.

3.Математикалық күтім мен кездейсоқ шаманың дисперсиясына анықтама бер. Ықтималдық теориясында кездейсоқ шамаларды дискретті және үздіксіз деп бөледі. Дискретті кездейсоқ шама шекті немесе санаулы сандар мәніне ие болады.Бұл сандар жиынтығы немесе дискретті мәндерге ие функция болуы мүмкін. Үздіксіз кездейсоқ шама үздіксіз мәндер жиынтығына ие болады.Көп қайталанған өлшеу нәтежиелері Үздіксіз кездейсоқ шамалар,өйткені өлшеу кезінде белгілі бір интервалдағы кез келген мәндер алынуы мүмкін.

Кездейсоқ шаманың ықтималдық арқылы табылған арифметикалық ортасын математикалық күтім деп атайды.Математикалық күтім , биномдық үлесу үшін 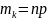Егер, p=q, онда математикалық күтім ең ықтимал мәнге ие болады.

Дисперсия ықтималдығын ескере отырып алынған кездейсоқ шаманың математикалық күтімнен ауытқуларының квадраттарының орташа мәні. 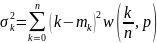. Дисперсия шама мәндерінің орта мәннен шашырауын сипаттайды.Биномдық үлесу үшін 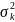=npq.

4.Термоэлектрлік термометрдің жұмыс істеу принципін түсіндір. Т.т.артықшылықтары мен кемшіліктері.Термоэлектрлік термометр әртекті екі материалдан дәнекерленген,бір өткізгіштің үзілісіне милливольтметр енгізілген тізбекті құрайды.3- суретте термоэлектрлік термометр схемасы көрсетілген. Әртекті екі металдан жасалған 1 және 2 өткізгіштер ұштары А және B түйіндерінде дәнекерленген.

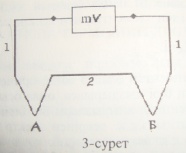
Өлшеу кезінде түйіннің біреуінің (мысалы,А) температурасы тұрақты ұсталып(t=0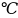 де еріп жатқан мұзы бар Дьюар ыдысына салынады),екінші ұшы (B) температурасы өлшенетін денеге жапсырылады.Осындай термометрлердің сұйықтық термометрлерден бір айырмашылығы ,термоқосақпен өте төмен немесе өте жоғары температураны өлшеуге болады,оның үстіне бұл термометрлер өте сезгіш келеді.Термоэлектрлік термометрдің т.э.қ.к шамасы А және B түйіндеріндегі э.қ.к. айырымымен анықталады және де ,егер А түйіннің температурасы t=0 болса ыстық түйіннің т.э.қ.к-інің температураға тәуелділігін төмендегідей өрнектейді:E=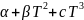 +… Мұнда 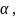және c термоэлектрлік термометр жасалған материалдар тегімен анықталатын тұрақтылар. Жаңадан жасалған Термоэлектрлік термометрді өлшеуге қолдану үшін алдыменен оны өлшемдеу керек,яғни екі түйін температураларының айырмасы мен түйіндер арасындағы туындайтын т.э.қ.к арасындағы тәуелділікті табу керек.Өлшемдеу кезінде температура мәні күні бұрын белгілі реперлік нүктелер:мұздың еру,судың қайнау,таза металдардың балқу температуралары пайдаланылады.Өлшемдеу кезінде термометрдің бір түйіні еріп жатқан мұз салынған Дьюар ыдысында термосталады да (түйіннің температурасы тұрақты болып қалады) ,екінші түйін кезегімен температуралары белгілі ортаға салынады.Термометрлік термометрлермен температураны дәлірек өлшеу үшін тізбектегі токты өлшегеннен гөрі тізбектегі т.э.қ.к өлшеген дұрыс болады.Өйткені , т.э.қ.к шамасы түйінді құрайтын метал өткізгіштер тегі мен түйіндер температурасымен ғана анықталса,электр тогы өлшеуіш құралдар,жалғау сымдар кедергілеріне және түйіндердің ішкі кедергісіне тәуелді болады.

Қос өткізгіштің термоэлектрлік қасиетін сипаттау үшін дифференциалдық т.э.қ.к 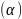деген ұғым енгізіледі. Дәнекерленген

қос өткізгіштер тегі мен температураға тәуелді болады және оның сандық мәні түйіндер арасындағы темп. айырымы t=1 кезінде туындайтын т.э.қ.к сандық мәніне тең. Т.э.қ.к тің температурадан тәуелділігін сызықтық функция деп алуға болады. Дәлірек өлшеу үшін бұл қатынасты квадраттық функция деп қарастырады. = 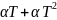.Бұл өрнекті y=A+Bx түріне келтірген қолайлы.Ол үшін өрнектің екі жағын да T-ға бөлсек: .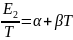

Осы теңдеудегі 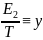, деп қабылдап y=A+Bx түріне келеміз.Осы теңдеудегі Aжәне B коефиценттері ең аз квадраттар әдісінде төмендегі өрнектер арқылы есептеледі: 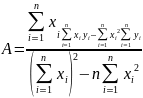, B=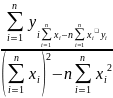

5. Зеебек эффектісі дегеніміз қандай эффект. Әр түрлі материалдан жасалған екі өткізгішті бір біріне тиістіргенде өткізгіштер арасында электрон алмасуы өтіп,осының салдарынан екі өткізгіштің тиісу нүктесінің жарсарларында потенциал айырмасы пайда болады.Соңғысының шамасы тиісіп тұрған өткізгіштер тегіне және тиісу нүктесінің температурасына тәуелді болады. Бір бірімен А және B нүктелерінде дәнекерленіп біріктірілген әртүрлі екі өткізгіштен тұратын электр тізбегін қарастырайық.

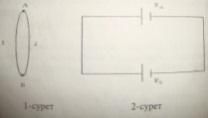
А және B түйіндерінің температуралары тең болса,осы нүктелер жапсарында пайда болатын потенциалдар айырмасы да тең болады.Осы тізбекке эквивлентті схема 2-суретте көрсетілген. Дәнекерленген түйіндерде (А және B) пайда болатын э.қ.к бір біріне қарсы қосылған тең элементтермен кескінделген: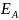 = 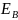.Мұндай тізбектегі электр тогы әрине нөлге тең.Егер екі түйіннің бірі қыздырылса,онда осы түйіндерде туындайтын потенциалдар айырмалары бір біріне тең емес,сондықтан қорытқы э.қ.к. әсерінен электр тогы пайда болады.Осы э.қ.к. термоэлектрлік қозғаушы күш деп аталады.Зеебек ашқан бұл құбылыс Зеебек эффектісі деп аталады. Зеебек эффектісі – түйіспелерінде әр түрлі температурасы бар әр текті өткізгіштерден тізбектеп құрастырылған электр тізбегінде электр қозғаушы күшінің пайда болуы. Оны 1821 жылы неміс физигі Т.И. Зеебек (1770 – 1831) ашқан. Терможұптың көмегімен температураны реттеу осы Зеебек эффектне негізделген.Термоэлектрлік термометр деп аталатын құралдарда температураны өлшеу үшін аталған құбылыс кеңінен қолданылады.

5.Зеебек эффектісі дегеніміз қандай эффект?

Әртүрлі материалдан жасалған екі өткізгішті бір-біріне тиістіргенде өткізгіштер арасында электрон алмасуы өтіп, осының салдарынан екі өткізгіштің тиісу нүктесінің жапсарларында потенциал айырмасы пайда болады. Соңғының шамасы тиісіп тұрған өткізгіштер тегіне және тиісу нүктесінің температурасына тәуелді болады. Бір-бірімен А және В түйіндерінде дәнекерленіп біріктірілген әртүрлі екі өткізгіштен тұратын электр тізбегін қарастырайық. А және В түйіндерінің температуралары тең болса, осы нүктелер жапсарында пайда болатын потенциалдар айырмасы да тең болады. Дәнекрленген түйіндерде пайда болатын э.қ.к. бір-біріне қарсы қосылған тең элементтермен кескінделген: . мұндай тізбектегі электр тоғы, әрине, нөлге тең. Егер екі түйіннің бірі қыздырылса, онда осы түйіндерде туындайтын потенциал айырмалары бір-біріне тең емес., сондықтан қорытқы э.қ.к. әсерінен электр тоғы пайда болады. Осы э.қ.к. термоэлектрлік қозғаушы күш д.а. Зеебек ашқан бұл құбылыс Зеебек эффектісі д.а. Оны 1821 жылы неміс физигі Т.И. Зеебек (1770 – 1831) ашқан.Термоэлектрлік термометр деп аталатын құралдарда темпаретураны өлшеу үшін аталған құбылыс кеңінен қолданылады.

6.Молекула-кинетикалық теорияның негізгі теңдеуінің мағынасын түсіндіріңіз.

Молекула-кинетикалық теория (МКТ) – заттардың молекулалық құрылысына негізделген жылу құбылыстару туралы ілім.МКТ-ның үш негізі бар:1) Барлық заттар – сұйық, қатты және газ күйіндегі – кішкентай бөлшектерден – молекулалардан, ал олар атомдардан құралады. Химиялық заттың молекулалары күрделі және жай болып, бір немесе бірнеше атомдардан құралады.2) Атомдар және молекулалар бейберекет қозғалыста болады.3) Молекулалар бір-бірімен өзара әсерлеседі. Бөлшектер арасындағы гравитациялық әсерлесу өте аз. МКТ-ның атомдардың бейберекет қозғалуының айқын экспериментальды көрінісі – броундық қозғалыс болып табылады. Броундық бөлшектер молекулалардың бейберекет соғылысуларынан қозғалады. Хаостық қозғалысынан оның соғылысулары модулі және бағыты жағынан ешқашан теңгерілмейді, сондықтан броундық бөлшектің жылдамдығы модулі және бағыты жағынан бейберекет өзгереді.Броундық қозғалыстың теориясын А. Эйнштейн жасады. Екі молекуланың арасындағы күштер олардың ара қарақашықтығына байланысты. Молекулалар оң және теріс  кеңістіктік күрделі структураларға ие болады. Егер молекулалардың арасындағы қашықтық үлкен болса, онда молекула арасындағы тартылыс күштері жеңеді, кішкентай арақашықтықта итеру күштері жеңеді. Қысым деп бiрлiк ауданға нормаль бойымен әсер ететiн күштi айтады. Қысым p әрпiмен белгiленiп, анықтамасы бойынша мынаған тең: p=F_n/S, мұнда S – бет элементiнiң ауданы, ал F_n – бет элементiне перпендикуляр әсер ететiн күш шамасы (1- сурет).  И деал газ жағдайында F_n нормаль күштiң шамасы келесi өрнекпен анықталады:  Бұл қатынастың қорытындысы.Газдың барлық молекулаларда v_x жылдамдық мәнi бiрдей бола бермейдi, олай болса қабырғаға әсер ететiн күштiң уақыт бойынша орта мәнi v²_x -қа емес, жылдамдықтарының орташа квадратына пропорционал:  . Жоғарыдағы формуланы ескере отырып, алатынымыз:  Анықтамасы бойынша p = F_n/S. Бұдан шығатыны,  = немесе = мұндағы m₀–газ молекуласының массасы,  – молекулалардың жылдамдықтары квадратының орта мәні, n – молекулалардың концентрациясы.Бұл молекула – кинетикалық теорияның негізгі теңдеуі болып табылады. Егер идеал газ молекулаларының ілгерілемелі қозғалысының кинетикалық энергиясының орта мәнін   арқылы белгілесек:  =  бұдан шығатыны = яғни идеал газ қысымы көлем бірлігіндегі молекулалардың ілгерілемелі қозғалысы орташа кинетикалық энергиясының үштен екісіне тең. 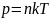бұл өрнек газ қысымы мен газ концентрациясы және абсолюттік температура арасындағы байланысты көрсетеді.

7.Температураның физикалық мағынасы? Больцман тұрақтысы туралы не білесіз?

Температура  макроскопикалық жүйенің термодинамикалық тепе-теңдік күйін сипаттайтын физикалық шама. Егер оқшауланған немесе тұйықталған жүйе термодинамикалық тепе-теңдік күйде болса, онда оқшауланған немесе тұйықталған жүйенің кез келген бөлігінде температура бірдей болады. Ал егер жүйе тепе-теңдік күйде болмаса, онда жылу (энергия) оның температурасы жоғары бөлігінен температурасы төмен бөлігіне қарай ауысып, белгілі бір уақыт өткеннен кейін жүйенің барлық бөліктеріндегі температура өзара теңеседі. Молекула кинетикалық теория тұрғысынан тепе-теңдіктегі жүйенің температурасы сол жүйені құрайтын атомдардың, молекулалардың, т.б. бөлшектердің жылулық қозғалысының қарқындылығын сипаттайды. Мысалы, классикалық статистикалық физиканың заңдарымен сипатталатын жүйе үшін бөлшектердің жылулық қозғалысының орташа кинетикалық энергиясы жүйенің абсолют температурасына тура пропорционал болады. Бұл жағдайда температура дененің жылыну (қызу) дәрежесін сипаттайды. Жалпы жағдайда температура жүйе энергиясының энтропия бойынша алынған туындысымен анықталады және ол әрқашан оң болады. Осылай анықталған температура абсолют температура немесетермодинамикалық шкала температурасы деп аталады. Бірліктердің халықаралық жүйесінде абсолют температураның бірлігіне кельвин (К) қабылданған. Көп жағдайда температураны Цельсий шкаласы (t) бойынша өлшейді. Ал t және Т бір-бірімен: t=T-273,15К теңдігі арқылы байланысқан (мұнда Цельсий градусы кельвинге тең). Дене температурасы термометр арқылы өлшенеді. Больцман тұрақтысы — іргелі физика тұрақтылардың бірі; газ тұрақтысының (R) Авогадро тұрақтысына (NA) қатынасына тең және k әрпімен белгіленеді: k  R/NA. Австрия физигі Л. Больцманның (1844 — 1906) құрметіне аталған. Больцман тұрақтысының сандық мәні: k1,380662(44) 10–23Дж/К (1984). Больцман тұрақтысы физиканың басты қатыстарының құрамына енеді (мысалы, идеал газ күйінің теңдеуі, т.б.), физика жүйе энтропиясын оның термодинамикалық ықтималдығымен байланыстырады. Больцман тұрақтысының шамасы сәуле шығару заңдарын тәжірибе жүзінде тексеру арқылы тікелей анықталады. ; ; ; ; ;

;

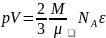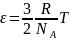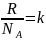8. Идеал газ күй теңдеуін келтіріңіз

Газ қысымының оның молекулаларының шоғырына және температурасына тәуелді болатыны аныкталды.Осы тәуелділік негізінде жеткілікті сиретілген газдың берілген массасының күйін сипаттайтын барлық үш макроскопиялық параметр р, V жэне Т-т байланыстыратын теңдеуді алуға болады. Бұл тендеу идеал газ күйінің теңдеуідеп аталады.Мына р = пкТ тендеуіне газ молекулалары шоғырына арналған өрнекті қоямыз, осы арқылы  газ шоғырын мына түрде жазуға болады:n=

мұндағы N_А —Авогадро тұрақтысы, m — газдың массасы, М — оның мольдік массасы. Жоғардағы теңдеуді р = пRТ теңдеуінің орнына қойсақ мынандай формола шығады:PV=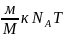  Мұндағы Больцман тұрақтысы к мен Авогадро тұрақтысы N_А -ның көбейтіндісін универсал (мольдік) газ тұрақтысы деп атайды жә­не оны R әрпімен белгілейд  R=1.38 Дж/K 1/моль=8.31Дж/(моль.К) PV=    

Бұл теңдеуде газдың тегіне тәуелді болатын бір ғана шама бар, ол — оның мольдік массасы.

Жоғадағы күй тендеуінен кез келген екі күйдегі идеал газдың кысымы, келемі және температурасы арасындағы байланыс келіп шығады.

Егер индекс 1-мен — екінші күйге катысты параметрлерді белгілесек, ал индекс 2-мен — екінші күйге қатысты параметрлерді белгілесек, онда жоғардағы теңдеуге сәйкес газдың берілген мас­сасы  ушін 

және  теңдеулерін  аламыз.Бұл тендеулердің, оң бөліктері бірдей. Демек, олардың сол бөліктері де тең болуға тиіс:  tБұл түрдегі күй тендеуі Клапейрон теңдеуі делінеді жә­не бұл күй тендеуін жазудың, бір түрі болып табылады. және     түріндегі күй теңдеуін бірінші рет ұлы орыс ғалымы Д. И. Менделеев алған. Сондықтан оны Менделеев - Клапейрон тендеуі деп атайды.

9. Адиабаттық процесс. Адиабата теңдеуі. Адиабата тұрақтысы туралы не білесіз?

термодинамикалық жүйеде оны қоршаған сыртқы ортамен жылу алмаспай ( ) орындалатын процесті адиабаттық  деп атайды. адиабаттық процесс үшін пуассон теңдеуі:  мұндағы    - адиабата көрсеткіші. пуассон теңдеуінің:

температура мен көлем арқылы жазылуы:  температура мен қысым арқылы жазылуы:

адиабаттық процесс үшін термодинамиканың бірінші бастамасы:  .

1)  , сыртқы күштердің жұмысы есебінен газдың ішкі энергиясы  артады,   яғни  .

2)  , газ ішкі энергиясының кемуі есебінен сыртқы күштерге  қарсы жұмыс атқарады, яғни  .   адиабаттық процесте атқарылатын жұмыс: 

         

10. Газдың парциал қысымы

1801 ж.  Дальтон заңы газ қоспасының қысымын және  жеке компоненттердің  жалпы қысымға  беретін  нақты «үлесін» анықтады. Парциал  қысым деп газ қоспасының әрбір газы осы көлемді жалғыз өзі алатын кездегі қысымды атайды.

11. 3-суреттегі 1-жұмыс сұйығы құйылған ыдыс (тостаған), 2-ұзына бойы шкала орнатылған көлбеу өлшеуіш түтік. Тостағанға тығыздығы р=809,5 кг/м3 этил спирті құйылады. Спирт деңгейі шкаланың «ноль» мәніне сәйкес келуі керек. Шкала ұзындығы мөлшермен 250/300 мм. Өлшеуіш түтіктің көлбеулігі абсолюттік мәні кіші қысымды өлшегенде аспап дәлдігін арттырады.

Егер объект қысымы атмосфера кысымынан үлкен болса, (Р>Ратм), объект тостағанға, керісінше болса (Р<Ратм) объект түтікке жалғанады.

Өлшенетін қысым әсерінен көлбеулік бұрышы α түтіктегі сұйық деңгейі вертикаль бағытта Һ2-ге төмендесін. Сонда, өлшенетін Р шамасын теңгеретін аспаптағы жұмыс сұйығы деңгейлерінің айырымы Һ: Һ=Һ1+Һ2

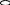
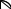
L Һ 1

Һ2

1 2

α

3-сурет. Көлбеу өлшеуіш шыны түтікті микроманометр сызбасы.

1-жұмыс сұйығы құйылған ыдыс (тостаған), 2-ұзына бойы шкала орнатылған өлшеуіш түтік. Егер түтіктегі сұйық бағанасының ұзындығы шкала бөліктерінің саны бойынша L (мм) десек, онда

Һ1= L*sin α

Түтіктегі сұйық көлемі тостағаннан ығысып шыққан сұйық көлеміне тең:

LS1=h2S2

S1-өлшеуіш түтіктің көлденең қима ауданы,

S2-тостағаннан көлденең қима ауданы,

Соңғы үш теңдеуді бірлестіре отырып шешкенде аларымыз:

Р=рgфh=рgфL(sin α+ S1/ S2),

Мұнда к=рgф(sin α+ S1/ S2)- аспап тұрақтысы.

Егер S1/ S2 <_1/400=0,0025 болса, онда

к= к1=рgф(sin α+ S1/ S2) және Р= к1* L (8)

L- мм-мен өлшенген бағана ұзындығы. к1-дің сандық мәндері (к1=0,2; 0,3; 0,4; 0,6; 0,8) көлбеу түтік бекітілетін (3) доғада көрсетілген (4-сурет). (8) өнректегі қысым бірліктер жүйесіне кірмейтін шамамен (кгс/м2) өлшенеді. Қысымды СИ жүйесінде алу үшін, (8) өрнекті Алматы қаласының географиялық ендігіне сәйкес келетін gф=9,804 м/с2 шамасына көбейту керек.

Сонымен, микроманометрмен өлшенген қысым СИ жүйесінде төмендегідей өрнекпен анықталады:

Р=gф к1* L , Па,

Немесе

Р=9,804к1* L , Па, Бұл жерде L мм-мен өлшенген.

Тостаған, өлшеуіш түтік, тұтік бекітілетін доға, қондырғы табаны, өлшеуіш түтіктің шкаласы, деңгей көрсеткіш, аспапты деңгей бойынша рететуші винт, сұйық ығыстырғыш (сұйық деңгейін реттеуші).

Аспап негізінен жұмыс сұйығы (спирт) құйылған тостаған (1) мен оған жалғанған өлшеуіш түтіктен (2) тұрады. Аспаптың барлық бөлшектері қондырғы табанына (4) бекітілген. Өлшеуіш түтіктің бес көлбеулік мәнені сәйкес келетін аспап тұрақтысы к1-дің сандық шамалары (к1=0,2; 0,3; 0,4; 0,6; 0,8) бекітуші доғада (3) жазылып қойылған. Өлшеуді бастамай тұрып, ығыстырғыштың (8) көмегімен көлбеу түтіктегі сұйық деңгейін шкала «нөліне» келтіру керек.

12. Фаза – деп заттың, жүйенің қалған бөліктерінен бөліну шекараларымен ажыратылған макроскопиялық біртекті бөлігі аталады, яғни оны жүйедегі механикалық жолмен бөліп алуға болады.

Температуралар мен қысымдардың теңдігі әлі де жүйенің тепе-теңдікте екендігін білдірмейді, себ., жанасатын фазалардың бір біріне өтуі мүмкін. Мұндай өтулер фазалық өтулер д.а. Зат қатты күйге сұйық күйден де, газ күйінен де келе алады. Осының екеуінде де зат құрылымында симметрия мүлдем болмайтын күйден симметриялы күйге ауысады (бұл тұжырым кристалдарда байқалатын алыс тәртіпке қатысты айтылып отыр).

Алдымен сұйықтың қатты затқа айналуын қарастыр. Сұйық заттың қатты күйге айналу процесі белгілі бір тұрақты температурада өтеді. Осы темп-ра кристализауия темп-сы (Тк) д.а. Тк-ның тұрақты болу себ., мынада: кристализация кезінде заттың молекулааралық н/е атомаралық әсерлесу потенциялық энергиясы кемиді (3), ал осының салдарынан бөлініп шыққан жылу «сұйық-кристалл» жүйесінің қоршаған ортаға беретін жылуын компенсациялайды. Осы жылуды кристализация жылуы д.а. Кристализация кезінде заттың бірлік массасынан бөлініп шығатын жылуды меншікті кристализация жылуы д.а. Кристализацияға кері процесс-балқу да тұрақты балқу темп-да (Тб) өтеді. Балқу кезінде жүйе энергия бөліп шығармайды, керісінше-коршаған ортадан энергия жұтады. Жұтылған энергия кристалдық торды бұзуға жұмсалады. Осныдай процестерді-бірінші текті фазалық ауысу д.а. Сонымен, бірінші түрдегі фазалық өту (мыс: балқу, кристализация және т.б.) фазалық өті жылуы д.а-н жылуды жұту н/е шығарумен қатар жүретін фазалық өту. Темп-ның тұрақтылығымен, энтропия мен көлемнің өзгеруімен сип-ды.

13. Зат қатты күйге сұйық күйден де, газ күйінен де келе алады. Осының екеуінде де зат құрылымында симметрия мүлдем болмайтын күйден симметриялы күйге ауысады (бұл тұжырым кристалдарда байқалатын алыс тәртіпке қатысты айтылып отыр).

Алдымен сұйықтың қатты затқа айналуын қарастыр. Сұйық заттың қатты күйге айналу процесі белгілі бір тұрақты температурада өтеді. Осы темп-ра кристализауия темп-сы (Тк) д.а. Тк-ның тұрақты болу себ., мынада: кристализация кезінде заттың молекулааралық н/е атомаралық әсерлесу потенциялық энергиясы кемиді (3), ал осының салдарынан бөлініп шыққан жылу «сұйық-кристалл» жүйесінің қоршаған ортаға беретін жылуын компенсациялайды. Осы жылуды кристализация жылуы д.а. Кристализация кезінде заттың бірлік массасынан бөлініп шығатын жылуды меншікті кристализация жылуы д.а. Кристализацияға кері процесс-балқу да тұрақты балқу темп-да (Тб) өтеді. Балқу кезінде жүйе энергия бөліп шығармайды, керісінше-коршаған ортадан энергия жұтады. Жұтылған энергия кристалдық торды бұзуға жұмсалады. Осныдай процестерді-бірінші текті фазалық ауысу д.а. Сонымен, бірінші түрдегі фазалық өту (мыс: балқу, кристализация және т.б.) фазалық өті жылуы д.а-н жылуды жұту н/е шығарумен қатар жүретін фазалық өту. Темп-ның тұрақтылығымен, энтропия мен көлемнің өзгеруімен сип-ды.

Балқу темп-да заттың бірлік массасы қатты күйден айналдыру үшін қажетті энергия мөлшері меншікті балқу жылуы д.а.

Кристализация кезінде бөлініп шыққан жылу денеден осы уақыт ішінде қоршаған ортаға берілген жылуға тең:

Q=g(Tk-Tf)(ta-T6), (10)

g=g1+g2/2 – қоршаған ортаға жылу берудің орташа жылдамдығы;

T6 және ta – крист/ция басталған және аяқталған уақыт мезеттері.

(9) бен (10) өрнектердің оң жақтарын теңестірсек

ƛm0=g(Tk-Tf)( ta-T6) осыдан ƛ=g(Tk-Tf)( ta-T6)/ m0

g- ді табу үшін (3) пен (8)-ден

g1= к1(C01m0+CTmT), g2=k2 (C02m0+CTmT),

яғни,

g= 1/2[k1(C01m0+CTmT)+k2 (C02m0+CTmT)]

сонымен, ƛ үшін түбегейлі соңғы өрнек былай жазылады.

ƛ=(Tk-Tf)(ta-T6)/ 2m0*[k1(C01m0+CTmT)+k2 (C02m0+CTmT)], (14)

k1, k2, ta, T6 эксперимент нәтижелері бойынша тұрғызылған графиктен (1-суреттегі графикке ұқсас табылады).

Ол үшін T6, уақыт мезеті үшін (5) теңдеуді анық.

In(Tk-Tf)=In(T0-Tf)-k1 T6 (15)

Одан: [In(T0-Tf)- In(Tk-Tf)/ T6] (16)

Осылай, ta және t2 моменттері үшін

k2- In(Tk-Tf)- In(T2-Tf)/( t2- ta).

Тәжірибе кезінде термоқосақпен –өлшенетін темп. Айырымының бүкіл өзгеріс интервалында термоқосақта пайда болатын термоэлектрлік қозғаушы күш (Е) термоқосақ түйіндері арасындағы темп. айырымына (∆Т) тура пропорционал

Е=а∆Т (а-тұрақты)

Деп жорамалдасақ, 2-суреттегі InЕ =Inа+In∆Т н/е InЕ=С+ In∆Т

С-тұрақты шама.

14. күй фунциясы болып табылатын энтропия мына формуламен анықт:

S=KБInΏ

Мұнда KБ – Больцман тұрақтысы, Ώ – термодинамикалық ықтималдық, (н/е статистикалық аймақ), яғни осы макроскопиялық күйге сәйкес келетін микрокүйлердің саны.Термодинамикалық ықтималдық, әрине, энтропия да, жүйенің күй параметрлерінің функциясы болып табылады. Сондықтан зат балқығанда, не сипатталғанда заттың энтропиясы өзгеру керек.

Жылулық процестердегі энтропия өзгерісін өлшеу кездегі келтірілген жылу шамасын өлшеуге негізделген.

Келтірілген жылу шамасы деп жүйе алмасқан энтроптар жылудың осы алмасу кезіндегі темп/ға қайнауын айтады.

Сонымен, dS=dQ/T (21)

Жүйе бір күйден 2 күйге өткенде энтропияның өзгерісі:

2

g(S)=S(I)=∫ dQ/T (22)

1

Оның ішінде, кристалдану (балқу) кезіндегі энтропия өзгерісі (2,3-сур/ге сәйкес) төменгі форм/мен анықталады: g(S)=S(B)= ∆S= ƛ*m/Tk

16. Кез келген дененің жылдамдығы С осы дененің темпр/сын 1 Кельвинге өзгерту үшін қажет жылуға тең. егер дене темп/сы dT-ға өзгерсе, жылусиымдылық

С=dQ/dT

Бұл жерде dQ –дене темп-сын dT-ға өзгерту үшін жұмсалған жылу шамасы. Жылусиымдылық өлшемі – Дж/К. Осы дене жасалған массалық жылусиымдылық енгізіледі:

Cm=C/m=dQ/m*dT, Дж/кг*К.

(2)-ден көрініп тұрғандай, меншікті массалық жылусимдылық заттың 1кг массасының темп/сын 1К-ге өзгерту үшін қажет жылуға тең. Бір моль затқа қатысты жылусиымдылықты меншікті мольдік жылусиямдылық д.а.

Cμ=C/V=dQ/V*dT, Дж/моль*К

V- заттың моль саны.

Сонымен, меншікті массалық немесе меншікті мольдік жылусиымдылық дененің өзін емес, денені құрайтын заттың жылулық қасиетін сипаттайды. Молекулалық физикада көбінесе меншікті мольдік жылусиымдылықты қолданамыз (2).

Жылусиымдылық денені қыздыру кезіндегі процесс түріне байланысты болады. Оның ішінде тұрақты қысым кезіндегі изобаралық жылусиымдылық Ср және тұрақты көлем кезіндегі изохоралық жылусиымдылық СV физикада пайдал/дыжәне де:

С V=(dQ/dT)V=Cp=(dQ/dT)p (3)

Газ үшін изобаралық жылусиымдылық Ср изохоралық жылусиымдылықтан үлкен болады (Ср>СV). Оның себебі мынада: изохоралық процесте келтірілген жылу тек газдың ішкі энергиясын өзгерту үшін ғана жұмсалса (изохоралық процесте жұмыс атқарылмайды), изобаралық процесте газ бұған қоса ұлғаю жұмысын атқарады.

Заттың жылусиымдылығы оның ішкі құрылысына тәуелді және оның заттың ішкі құрылымы туралы белгілі бір болжамдар негізінде теория жүзінде есептеуге болады. Молекуланың еркіндік жәрежелері бойынша энергияның тең үлесу заңына негізделген классикалық теория Ср және СV қатынасы үшін:

Ƴ=Cp/Cv=1+2/i.

Мұндағы i- еркіндік дәрежелер саны.

(4) өрнекке сәйкес, Ƴ шамасы молекуланың еркіндік дәреже санымен анықталады. Механикалық жүйенің еркіндік дәреже саны деп осы жүйенің кеңістіктегі орны және конфигурациясын анықтайтын тәуелсіз координаттар санын айтады. Бір атомдық газ үшін i=5, үш атомдық молекуланың еркіндік дәреже саны i=6 (молекула атомдары қатаң байланыста).

17. Квазистационарлық режим дегеніміз не? Квазистационарлық өрістерді талдау кезінде өткізу тоқтармен салыстырғанда жылжу токтарды есепке алмасада болады. Максвелл теңдеулерінен шығатын квазистационарлық өріс негізгі теңдеулерінің жүйесі мына түрде жазылады

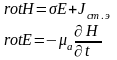(1.17)

1.2 сурет

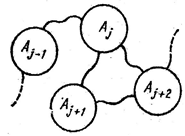
Маңызды жүйелер ол квазистационарлық жағдайға сәйкес, тізбекті структуралар болады (1.2 сурет). Олар үшін бір бірімен өткізгіштер жүйесімен жалғанған көптеген кеңістікті аймақтардың Аj(j -1,2,...) бар екені сипат болып тұр. Тізбекті стуктуралар өткізгіштер жүйесінің кеңістікті деформапияларына қатысты инвариантты болады. Осы жағдай тізбекті структурадан оның абстракті моделіне - тізбектер теориясының әдістері арқылы талдауға болатын принципиалды электрлік сұлбаға көшу мүмкіндік береді.

Квазистационарлық әдістердің іске асуының екінші жағдайы - жақсы өткізетін (металлдың) ортадағы электрмагниттік ауытқылар таралу порцессін зерттеу. Өткізу тоқтың тығыздығы Јпр =σЕ жылжу тоқтың тығыздығынан Јсм=ωεаЕ едәуір артық болады. Бұл кезде (1.18) жүйеден екінші реттік дифференциалдық теңдеулер шығады

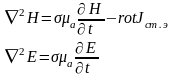(1.18)

Толқындық теңдеулерге қарағанда берілген теңдеулерге уақыт бойынша бірінші туынды пайда болып отыр.

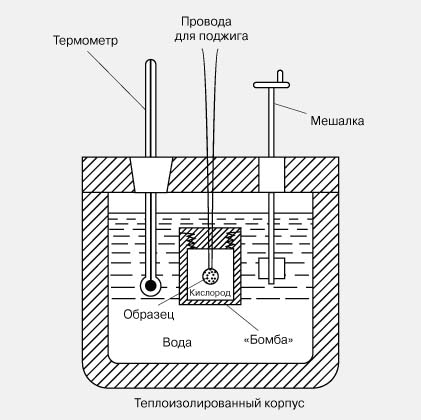
18. Калориметрден қоршаған ортаға кететін жылу шығыны қалай ескеріледі?

Калориметр (латынша: calor - жылу, ыстық және метр) — әр түрлі физикалық, химиялық және биологиялық процестер кезінде денелерден бөлінетін немесе олардың қабылдайтын жылу мөлшерін өлшейтін аспап.

19. Жанама үйкеліс кернеуі дегеніміз не ? Сұйық тұтқырлығын сипаттайтын Ньютон заңын жазыңыз.

Барлық наќты газ бен сұйыќтарѓа тән ќасиет оның тұтқыр болуы немесе ішкі үйкелістің болуы. Егер А жєне О немесе О жєне В жазыќтыќтармен шектелген аралыќта газ (сұйыќ) аѓысы баѓытта байќалса, онда газ аѓыныныњ жылдамдыѓы ќабаттарды бµліп тұрѓан бетке перпендикуляр баѓытында ќабаттан ќабатќа µзгеріп отырады, демек (8.3-сурет). Мұндай құбылысты єр түрлі ќабаттаѓы сұйыќтыњ бөлшектерініњ жылдамдыѓын зерттегенде түсінуге болады. Жазыќтыќтарѓа тікелей жанасќан бөлшектер, оларѓа жабысып ќалѓан-дай болады, егер жазыќтыќтар ќозғалмаса, онда “жабысќан” бөлшек-тер ќозѓалысќа ұшырамайды, ал керісінше ќозѓалыста болса – жазыќтыќтардыњ жылдамдыѓындай жылдамдыќќа ие болады. Ењ ұлкен жылдамдыќтыњ мєні осы жазыќтыќтар арасында орналасќан сұйыќтыњ (газдың) ортасында байќалады; неѓұрлым жазыќтыќтар бетіне жаќындаѓан сайын жылдамдыќ кішірейе береді, тікелей беттік ќабаттаѓы “жабысќан” бөлшектер ќозѓалмайды.

Мысалы, 8.3-суреттегі ќабаттар дµњгелек түтіктің ойша алынѓан ќабырѓаларыныњ беті деп есептесек, онда кез келген ќабаттыњ радиусы бойындаѓы жылдамдыќ былай өзгеретінін көрсетуге болады:

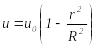, (8.24)мұндаѓы – түтіктің радиусы, – түтіктің (сұйыќ ќабатыныњ орта-сы) ортасындаѓы жылдамдыќ, – түтіктіњ ортасынан ќашыќтыќ-таѓы жылдамдыќ. Сондыќтан, 8.3-суреттегі жылдамдыќтардыњ түтік бойымен ОА жазыќтыќтармен шектелген аралыќта таралу кескіні парабола тєріздес, мұндаѓы сызыќтардыњ тілшіктерініњ ұшы газдыњ жылдамдыќтарыныњ векторын көрсетеді.

Бұндай аѓыста газдың ортасындаѓы жоѓары ќабаттан, жылдам-дыѓы кіші, баяу ќозѓалатын ќабаттарѓа импульстің тасымалдауы байќалады. Газ аѓыныныњ жылдамдыѓыныњ ќабаттан ќабатќа өзгеруі, жылдамдыќтыњ градиентініњ пайда болуына єкеледі. Сондыќтан, ќатар жатќан газдыњ єр түрлі жылдамдыќпен ќозѓалатын екі ќабатының арасындаѓы шекарада ішкі үйкеліс күші әсер ететін болады, оныњ шамасы тµмендегідей эмпирикалыќ формуламен аныќталады: , (8.25)мұндаѓы – газдыњ ќатар көршілес жатќан ќабаттарын бөлетін жазыќтыќтыњ бірлік ауданына түсірілген күш; – тұтќырлыќ коэффициенті немесе ішкі үйкеліс коэффициенті деп аталады.

Бұл теңеуді И.Ньютон таѓайындаѓан, егер деформациялану жылдамдыѓына тєуелсіз болса, дєл орындалады. Газдыњ (сұйыќтыњ) єр түрлі ќабаттарыныњ жылдамдыѓы осы тұтќырлыќ (немесе ішкі ұйкеліс) деген ќасиетініњ арќасында теңеледі. Соның нєтижесінен ортаның деформациялану жылдамдыѓына тєуелді кернеуліктер пайда болады.

Осыдан тұтќырлыќ коэффициентініњ сандыќ мєні жылдамдыќ градиенті бірге тењ болѓанда, бірлік ауданѓа єсер ететін күшке тењ. Бұл коэффициенттіњ СИ жүйесіндегі өлшем бірлігі .

Бұл жаѓдайда газдыњ әрбір молекуласы екі түрлі ќозѓалысќа ќаты-сады: орташа жылдамдыѓы хаосты жылулыќ ќозѓалысќа жєне газдың аѓыныныњ жылдамдыѓына ие болады. Сондыќтан єр молекула жылдамдыѓы әр түрлі бір ќабаттан екінші ќабатќа жылулыќ ќозѓалыстыњ єсерінен µткенде, өзара соќтыѓысулар нєтижесінде импульспен алмасады. Бұл импульспен алмасу процесі газдыњ єр түрлі ќабаттарыныњ аѓын жылдамдыѓын теңестіреді.

Сөйтіп, бұндай газдаѓы өтетін тасымалдау процесі импульстіњ – компонентініњ градиентініњ шамасымен аныќталады. Сондыќтан, (+z) баѓытта О жазыќтыќтыњ бірлік ауданын бірлік уаќытта ќиып өтетін -ның ќорытқы импульс аѓынының тыѓыздыѓын (8.12)-ні ескеріп, былай аныќтаймыз:

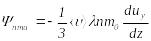. (8.26)(8.26)-шы µрнекті (8.25)-пен салыстырып, тұтќырлыќ коэффициен-тін аныќтайтын формуланы мына түрде жазамыз:

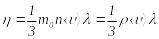, (8.27)

мұндаѓы – газдыњ тыѓыздыѓы, – молекула массасы, – еркін жүру жолыныњ орташа ұзындыѓы.

(8.27)-ші формула бойынша болѓандыќтан, тұтќырлыќ коэффициенті температураға байланысты шамасына пропор-ционал µседі. , ал , олай болса, элементар кинетикалыќ теориясы бойынша тұтќырлыќ коэффициенті ќысымѓа тєуелсіз болады.