2. Параметры сетевой модели и методы их расчета

Введем следующие обозначения:

i, j - номера событий;

N - количество событий;

(i,j) – работа, соединяющая события i,j;

t (i,j) - продолжительность работы, соединяющей события i и j;

- критический путь;

Использование. этого резерва не влияет на величину резер-вов времени других работ.

Путь сетевой модели характеризуется двумя показателями:

1. Продолжительность пути определяется суммой продолжительностей составляющих его работ.

2. Резерв времени пути показывает, на сколько может увеличиться продолжительность работ, составляющих путь , без изменения продолжительности общего срока выполнении всех работ:

Работы, лежащие на критическом пути, резервов времени не имеют.

Определить степень трудности выполнения в срок каждой группы работ некритического пути можно с помощью коэффициента напряженности работ (i, j). Если совпадающую с критическим путем величину отрезка пути обозначить как , а протяженность максимального из некритических путей, проходящих через данную работу, - (i, j), то

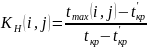
Коэффициент напряженности работы можно рассчитать и через резерв времени:

Коэффициент напряженности изменяется от 0 до 1, причем чем он ближе к 1, тем сложнее выполнить данную работу в установленный срок. Самыми напряженными являются работы критического пути, для которых он равен 1. На основе этого коэффициента все работы разделяются на три группы:

1) напряженные, когда > 0,8;

2) подкритические, когда 0,6 0,8;

3) резервные, когда 0,6.

Оптимизация сетевой модели заключается в перераспределении ресурсов с напряженных работ на критические, в результате чего максимально уменьшается общая продолжительность работ и все переводится в первую группу.

Пример. Рассмотрим задачу о минимизации времени выполнения комплекса работ по переводу торгового предприятия на самообслуживание. Описание работ и их продолжительность представлены в таблице.

Работа (i,j)	Содержание работы	Потребность в ресурсах, i,j	Коэффициент перерасчета ресурсов,	Продолжительность работы, дни
(0,1)	Составление сметы	10	0,1	15
(1,2)	Приобретение оборудования	5	0,2	16
(1,3)	Подбор кадров	2	0,5	6
(2,4)	Монтаж оборудования	3,3	0,3	6
(3,5)	Подготовка кадров	1,6	0,6	5
(4,6)	Оформление зала	2,5	0,4	8
(5,6)	Доставка товаров	1,4	0,7	6
(5,7)	Заказ и получение специальной одежды	1,1	0,9	14
(5,8)	Заказ, получение и установка программного обеспечения	1	1	8
(6,8)	Выкладка товара	1,2	0,8	2
(7,8)	Заполнение базы данных по имеющимся товарам	0,9	1,1	4
(8,9)	Генеральная репетиция	0,8	1,2	3

Составим сетевой график для данной задачи

Рис 2.5 Сетевой график задачи перевода торгового предприятия на самообслуживание

Результаты расчета основных параметров модели оформим в виде таблицы:

Резерв времени	событий		10	0	0	7	0	7	0	0	0	9	0	0	0
	работ	Свободный,	9	0	0	0	0	0	0	13	7	0	0	9	0
Сроки выполнения работ		Полный,	8	0	0	7	0	7	0	13	7	9	0	9	0
	поздние	Окончание,	7	15	31	28	37	33	45	45	47	43	47	47	50
		Начало,	6	0	15	22	31	28	37	39	33	35	45	43	47
	ранние	Окончание,	5	15	31	21	37	26	45	32	40	34	47	38	40
		Начало,	4	0	15	15	31	21	37	26	26	26	45	34	37
Продолжительность работы t(I,j)			3	15	16	6	6	5	8	6	14	8	2	4	3
Колличество предшествующих работ			2	0	1	1	1	1	1	1	1	1	2	1	3
Работа (I,j)			1	(0,1)	(1,2)	(1,3)	(2,4)	(3,5)	(4,6)	(5,6)	(5,7)	(5,8)	(6,8)	(7,8)	(8,9)

Правила заполнения таблицы:

- столбцы 1 и 3 заполняются на основе исходных данныx, представленных в таблице;

- в столбце 2 записывается количество предшествующих работ, которое определяется либо по сетевому графику рис. 2.3, либо из столбца 1: определяем число работ, имеющих одинаковый номер завершения среди всех пар (i, j), например (4,6) и (5,6), и записываем это число (т.е. 2) в столбце 2 против работы (6,8), т.е. количества предшествующих работ;

- в столбце 4 раннее начало работ, выходящих из исходного состояния, равно 0. Раннее начало последующих работ равно максимальному сроку раннего окончания предшествующих работ. Количество сравниваемых сроков равно количеству предшествующих работ в столбце 2. Расчет показателей этого столбца проводится после расчета раннего окончания предшествующих работ, т.е. заполнения предшествующих строк столбца 5;

- в столбце 5 раннее окончание работ, выходящих из исходного события, равно их продолжительности. Ранее окончание последующих работ равно сумме величин раннего начала и продолжительности данной работы, т.е. значение столбца 5 равно сумме значений столбцов 3 и 4;

- перед заполнением столбца 7 необходимо рассчитать продолжительность критического пути как максимум из сроков раннего окончания работ, ведущих к завершающему событию 9 (в нашем случае это шаг{40+3; 47+3;38+ 3} = 50 дн.);

- заполнение столбца 7 ведется снизу вверх. Для всех работ, ведущих к завершающему событию, позднее окончание равно продолжительности критического пути ( (8,9) = 50). Затем находятся предшествующие работы; поздний срок их окончания будет равен разности позднего срока окончания текущей работы и продолжительности текущей работы (например, (7,8) = = (8,9) - = 50-3 = 47);

- столбец 6 заполняется после столбца 7. Позднее начало работы определяется как разность между поздним сроком окончания работы и ее продолжительностью, т.е. значение столбца 6 равно разности значений столбцов 7 и 3;

- в столбце 8 полный резерв времени работы определяется как разность между значениями етопбцов 7 и 5. Если эта разность равна 0, то работа является критической;

- в столбце 10 резерв времени событий j определяется как разность позднего окончания работы, заканчивающегося событием j столбца 7, и поздним началом работы, начинающейся событием j столбиа 4 (например, (5,8)= (6,8)= (7,8)=47-47=0;

- в столбце 9 свободный резерв времени работы определяется как разность значений столбцов 10 и 8 и указывает на расположения резервов, необходимых для оптимизации.

Для определения резервов времени составим все возможные пути перехода из исходного события (0) к завершающему (9). Таких путей четыре:

L₁ = [(0,1)(1,2)(2,4)(4,6)(6,8)(8,9)],

L₂ = [(0,1)(1,3)(3,5)(5,6)(6,8)(8,9)],

L₃ = [(0,1)(1,3)(3,5)(5,8)( 8,9)],

L₄ = [(0,1)(1,3)(3,5)(5,7)(7,8)(8,9)].

Определим длительность этих путей:

Найдём длину критического пути:

Определим полные резервы времени по всем путям:

Расчитаем коэффициенты напряжённости. Для работ критического пути они будут равны 1, для других работ определим их значение. В результате получим:

В соответствии с полученным значением коэффициентов напряженности, можно утверждать, что оптимизация в сетевой модели возможно за счет свободных резервов работ (5,6), (5,8) и (7,8), а также за счет остальных резервов работ (1,3), (3,5) и (5,7).