
- •Лекция 2 Методы математического описания линейных элементов асу
- •1. Обобщенная структурная схема асу с обратной связью
- •2. Структура и структурные схемы асу
- •Моделирование в тау
- •Связь входа и выхода элемента асу
- •Линейность и нелинейность
- •Линеаризация уравнений
- •Линейная интерполяция
- •Линеаризация с помощью ряда Тейлора
Линеаризация уравнений
Выгоды линейности бывают столь велики, что приближенная замена нелинейных соотношений на линейные, нелинейных моделей на линейные, т. е. линеаризация соотношений, моделей и т. д. весьма распространена в моделировании.
Рассмотрим вначале два наиболее часто используемых случаев линеаризации: либо если эксперимент показывает (как, например, для закона Гука), что отклонение от линейности в рассматриваемом диапазоне ab изменения переменных невелико и несущественно (рис.6.1,а), либо же необходимо линеаризовать функцию в окрестности точки a (рис.6.1,б).
В первом случае используется линейная интерполяция, а во втором – линеаризация с применением ряда Тейлора.

Линейная интерполяция
Задача сводится к нахождению прямой, проведенной через две точки:
|
, (1) |
откуда
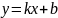 , где
, где
В общем случае линейную интерполяцию можно применить и для большего количества точек – в этом случае вместо кривой линии получаем ломаную линию, состоящую из последовательно соединенных прямых линий (рис.6.2).

Линеаризация с помощью ряда Тейлора
В этом случае функция y(x) раскладывается в ряд Тейлора в окрестности точки a (рис.6.1,б):
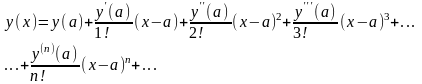
с отбрасыванием всех членов высшего порядка малости (в этом и состоит линеаризация):
|
|
где
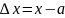 .
.
Второе слагаемое в (2) – дифференциал функции y(x) в точке a.
Пример. Исходная математическая модель является квадратным трехчленом:
 . (3)
. (3)
Необходимо линеаризовать эту модель в окрестности точки x=2.
Решение.
По (3) находим:
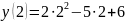 =4.
Производная
=4.
Производная
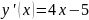 в
точке x=2
равна:
в
точке x=2
равна:
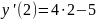 =3,
тогда линеаризованная модель
=3,
тогда линеаризованная модель
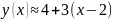 . (4)
. (4)
Сравним результаты расчетов по формулам (3) и (4):
Таблица 1
x |
|
|
Относительная погрешность,% |
2 |
4 |
4 |
0 |
2.01 |
4,03 |
4,03 |
0 |
2,04 |
4,123 |
4,12 |
0,07 |
2,1 |
4,32 |
4,3 |
0,46 |
2,5 |
6 |
5,5 |
8,3 |
Как видим, при малых отклонениях погрешности получаются незначительными.
К тому же, модель (4) проще, чем (3), но недостатком такого подхода является необходимость пересчета коэффициентов (фактически построение другой модели) при существенном изменении значения x (например, при x=3).

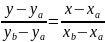

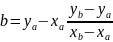
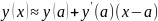 ,
(2)
,
(2)