ЭКЗАМЕН ИНФОРМАТИКА

1) Инфоpматика — это основанная на использовании компьютерной техники дисциплина, изучающая структуру и общие свойства информации, а также закономерности и методы её создания, хранения, поиска, преобразования, передачи и применения в различных сферах человеческой деятельности..

• pазpаботка вычислительных систем и пpогpаммного обеспечения;

• теоpия инфоpмации, изучающая процессы, связанные с передачей, приёмом, преобразованием и хранением информации;

• математическое моделирование, методы вычислительной и прикладной математики и их применение к фундаментальным и прикладным исследованиям в различных областях знаний;

• методы искусственного интеллекта, моделирующие методы логического и аналитического мышления в интеллектуальной деятельности человека (логический вывод, обучение, понимание речи, визуальное восприятие, игры и др.);

• системный анализ, изучающий методологические средства, используемые для подготовки и обоснования решений по сложным проблемам различного характера;

• биоинформатика, изучающая информационные процессы в биологических системах;

• социальная информатика, изучающая процессы информатизации общества;

• методы машинной графики, анимации, средства мультимедиа;

• телекоммуникационные системы и сети, в том числе, глобальные компьютерные сети, объединяющие всё человечество в единое информационное сообщество;

• разнообразные пpиложения, охватывающие производство, науку, образование, медицину, торговлю, сельское хозяйство и все другие виды хозяйственной и общественной деятельности.

Роль информатики в развитии общества чрезвычайно велика. С ней связано начало революции в области накопления, передачи и обработки информации. Эта революция, следующая за революциями в овладении веществом и энергией, затрагивает и коренным образом преобразует не только сферу материального производства, но и интеллектуальную, духовную сферы жизни. 2)Информация – это обозначение содержания, полученного из внешнего мира в процессе нашего приспособления к нему и приспособления к нему наших чувств. 3) 1 байт=8 битов

1 килобайт (Кб)=1024 байта =2¹⁰ байтов

1 мегабайт (Мб)=1024 килобайта =2¹⁰ килобайтов=2²⁰ байтов

1 гигабайт (Гб)=1024 мегабайта =2¹⁰ мегабайтов=2³⁰ байтов

1 терабайт (Гб)=1024 гигабайта =2¹⁰ гигабайтов=2⁴⁰ байтов

• 4) Сохранить, передать, создать – что можно делать с информацией 5) Информационные ресурсы — это идеи человечества и указания по их реализации, накопленные в форме, позволяющей их воспроизводство. Информационная технология — это совокупность методов и устройств, используемых людьми для обработки информации. Обработка информации, это кодирование, декодирование, передача, прием, просмотр и редактирование информации. Обработка происходит в несколько этапов. Во-первых: Ввод информации, во-вторых: кодирование информации ( в машинный язык ), в-третьих: прием и декодирование информации в удобный для чтение формат. 6) Систе́ма счисле́ния — символический метод записи чисел, представление чисел с помощью письменных знаков. Система счисления: * даёт представления множества чисел (целых или вещественных) * даёт каждому числу уникальное представление (или, по крайней мере, стандартное представление) * отражает алгебраическую и арифметическую структуру чисел. Системы счисления подразделяются на позиционные, непозиционные и смешанные. - В позиционной системе счисления количественное значение каждой цифры зависит от ее местоположения (позиции) в числе(т.е система счисления, в которой важную роль играет порядок следования цифр. Каждая цифра в позиционной записи имеет свою позицию, которая определяет её численное значение. Позиции цифр носят название разрядов.) - В непозиционной системе счисления цифры не меняют своего количествен-ного значения при изменении их положения в числе(т.е Непозиционная система счисления — это такая система счисления, в которой положения цифры в записи числа не зависит величина, которую она обозначает. Система может накладывать определенные ограничения на порядок цифр (расположение по возрастанию или убыванию)). Специалисты используют систему счисления: двоичная (используются цифры 0, 1);

• восьмеричная (используются цифры 0, 1, ..., 7);

• шестнадцатеричная (для первых целых чисел от нуля до девяти используются цифры 0, 1, ..., 9, а для следующих чисел — от десяти до пятнадцати — в качестве цифр используются символы A, B, C, D, E, F).

7) и предпочитают десятичную систему, вероятно, потому, что с древних времен считали по пальцам, а пальцев у людей по десять на руках и ногах. Не всегда и не везде люди пользуются десятичной системой счисления. В Китае, например, долгое время пользовались пятеричной системой счисления.

А компьютеры используют двоичную систему потому, что она имеет ряд преимуществ перед другими системами:

• для ее реализации нужны технические устройства с двумя устойчивыми состояниями (есть ток — нет тока, намагничен — не намагничен и т.п.), а не, например, с десятью, — как в десятичной;

• представление информации посредством только двух состояний надежно и помехоустойчиво;

• возможно применение аппарата булевой алгебры для выполнения логических преобразований информации;

двоичная арифметика намного проще десятичной. Преимущества и недостатки двоичной системы счисления: +проще -по обьему больше 8) Пользуются таблицей умножения, сложение выполняют, используя правила переноса в старший разряд.

Для двоичной системы: 1+0=1; 1+1=10₍₂₎;

Для восьмеричной системы: 1+7=10₍₈₎.

Для шестнадцатеричной системы: F+1=10₍₁₆₎ (15₍₁₀₎=F₍₁₆₎)

Сложить два двоичных числа:

+

 10111

При вычитании необходимо помнить, что занятая в ближайшем старшем разряде единица дает две единицы младшего разряда. Если в соседних старших разрядах стоят нули, то приходится занимать единицу через несколько разрядов. При этом единица, занятая в ближайшем старшем разряде, дает две единицы мл. разряда и единицы во всех нулевых разрядах, стоящих между мл. и тем ст. разрядом, в кот. Бралась единица.

Произвести вычитание

-

 10

 

Умножение

10111,01

×

10,11

10111 01

10111 01

10111 01

111111,1111

 

Деление

 

110101110/1010

- 101011

1010

1010

1010

1010

 

 

* Основание-сколько символов всего в данной СС и сколько символов младшего разряда занимается в символе старшего разряда.

9) ля перевода чисел из десятичной системы счисления в двоичную используют так называемый "алгоритм замещения", состоящий из следующей последовательности действий:

1. Делим десятичное число А на 2. Частное Q запоминаем для следующего шага, а остаток a записываем как младший бит двоичного числа.

2. Если частное q не равно 0, принимаем его за новое делимое и повторяем процедуру, описанную в шаге 1. Каждый новый остаток (0 или 1) записывается в разряды двоичного числа в направлении от младшего бита к старшему.

3. Алгоритм продолжается до тех пор, пока в результате выполнения шагов 1 и 2 не получится частное Q = 0 и остаток a = 1.

Например, требуется перевести десятичное число 247 в двоичное. В соответствии с приведенным алгоритмом получим: 

24710 : 2 = 12310

24710 - 24610 = 1, остаток 1 записываем в МБ двоичного числа.

12310 : 2 = 6110

12310 - 12210 = 1, остаток 1 записываем в следующий после МБ разряд двоичного числа.

6110 : 2 = 3010

6110 - 6010 = 1, остаток 1 записываем в старший разряд двоичного числа.

3010 : 2 = 1510

3010 - 3010 = 0, остаток 0 записываем в старший разряд двоичного числа.

1510 : 2 = 710

1510 - 1410 = 1, остаток 1 записываем в старший разряд двоичного числа.

710 : 2 = 310

710 - 610 = 1, остаток 1 записываем в старший разряд двоичного числа.

310 : 2 = 110

310 - 210 = 1, остаток 1 записываем в старший разряд двоичного числа.

110 : 2 = 010, остаток 1 записываем в старший разряд двоичного числа.

Таким образом, искомое двоичное число равно 11110111₂. 

В восьмеричную: Итак в десятичной системе счисления мы пользуемся 10 цифрами с помощью которых можем составить любое число. Это цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.

В восьмеричной системе счисления у нас только восемь цифр 0, 1, 2, 3, 4, 5, 6, 7, с помощью которых мы можем составлять любые числа.

В восьмеричной системе счисления после семерки идет цифра 10 т.к. цифры 8 в ней нет. Почему? А потому что когда мы работаем в десятичной системе счисления то когда доходим до 9 то при прибавлении к ней единицы 9+1 получаем, что 9 заменяется на ноль, слева от которого добавляется 1 (к старшему разряду).

Таким образом мы можем попробовать составить небольшую таблицу соответствия чисел десятичной и восьмиричной системы счисления.

Десятичная	Восьмеричная
1	1
2	2
3	3
4	4
5	5
6	6
7	7
8	10
9	11
10	12
11	13
12	14
13	15
14	16
15	17
16	20
17	21
18	22
19	23
20	24
21	25
22	26
23	27
24	30
25	31
26	32
27	33
28	34
29	35
30	36
31	37

 

То есть, смотрите, когда мы выписывали правый столбец (числа в восьмеричной системе счисления) мы руководствовались тем правилом, которое описали выше таблицы. Как только у нас заканчиваются цифры системы счисления мы пишем ноль и добавляем единицу к старшему разряду.

А теперь рассмотрим как перевети число из десятичной системы счисления в восьмеричную. Давайте возьмем число 259 в десятичной системе счисления.

Число в десятичной системе счисления делим на основание степени (восьмерку). Получаем какую то целую часть и остаток. Если целая часть больше либо равна 8, то опять делим на основание степени и получаем целую часть и остаток. Как только целая часть становится меньше восьми, начинаем выписывать, сначала последнюю целую часть, а затем все остатки в обратном порядке. Это и будет число в новой системе счисления, в нашем случае в восьмиричной.

И сделаем обратное преобразование переведем число 403 в восьмеричной системе счисления в десмятичную.

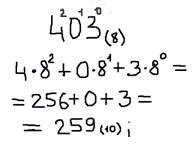
То есть вначале мы нумеруем числа справа налево для того, чтобы затем каждое из чисел в восьмиричной системе счисления умножить на восьмерку в соответствующей степени. Сложив все, мы получим результат в десятичной системе счисления.

В шестнадцатиричную: Для перевода чисел из десятичной системы счисления в шестнадцатеричную используют тот же "алгоритм замещения", что и при переводе из десятичной системы счисления в двоичную и восьмеричную, только в качестве делителя используют 16, основание шестнадцатеричной системы счисления:

1. Делим десятичное число А на 16. Частное Q запоминаем для следующего шага, а остаток a записываем как младший бит шестнадцатеричного числа.

2. Если частное q не равно 0, принимаем его за новое делимое и повторяем процедуру, описанную в шаге 1. Каждый новый остаток записывается в разряды шестнадцатеричного числа в направлении от младшего бита к старшему.

3. Алгоритм продолжается до тех пор, пока в результате выполнения шагов 1 и 2 не получится частное Q = 0 и остаток a меньше 16.

Например, требуется перевести десятичное число 32767 в шестнадцатеричное. В соответствии с приведенным алгоритмом получим: 

3276710 : 16 = 204710

3276710 - 3275210 = 15, остаток 15 в виде F записываем в МБ шестнадцатеричного числа.

204710 : 16 = 12710

204710 - 203210 = 15, остаток 15 в виде F записываем в следующий после МБ разряд шестнадцатеричного числа.

12710 : 16 = 710

12710 - 11210 = 15, остаток 15 в виде F записываем в старший разряд шестнадцатеричного числа.

710 : 16 = 010, остаток 7 записываем в старший разряд шестнадцатеричного числа.

Таким образом, искомое шестнадцатеричное число равно 7FFF₁₆. 

10) В восьмеричную: Задача перевода чисел из двоичной системы счисления в десятичную чаще всего возникает уже при обратном преобразовании вычисленных либо обработанных компьютером значений в более понятные пользователю десятичные цифры. Алгоритм перевода двоичных чисел в десятичные достаточно прост (его иногда называют алгоритмом замещения):  Для перевода двоичного числа в десятичное необходимо это число представить в виде суммы произведений степеней основания двоичной системы счисления на соответствующие цифры в разрядах двоичного числа. 

Например, требуется перевести двоичное число 10110110 в десятичное. В этом числе 8 цифр и 8 разрядов ( разряды считаются, начиная с нулевого, которому соответствует младший бит). В соответствии с уже известным нам правилом представим его в виде суммы степеней с основанием 2: 

10110110₂ = (1·2⁷)+(0·2⁶)+(1·2⁵)+(1·2⁴)+(0·2³)+(1·2²)+(1·2¹)+(0·2⁰) = 128+32+16+4+2 = 182₁₀

Из этого примера видно, в частности, что десятичная система счисления более компактно отображает числа - 3 цифры (т.е. бита) вместо 8 цифр в двоичной системе счисления. Для вычислений "вручную" и решения примеров и контрольных заданий вам могут пригодиться таблицы степеней оснований изучаемых систем счисления (2, 8, 10, 16), приведенные в Приложении.  Шестнадцатиричную: ПЕРЕВОД ИЗ ДВОИЧНОЙ В ШЕСТНАДЦАТИРИЧНУЮ 

Пеpевод из двоичной системы исчисления в 16-тиричную осуществляется по таблице для каждых 4-х двоичных единиц:

0000=0 0001=1 0010=2 0011=3 0100=4 0101=5 0110=6 0111=7 1000=8 1001=9 1010=A 1011=B 1100=C 1101=D 1110=E 1111=F Например: число 111010110 = 0001'1101'0110 = 1D6

А вот алгоритм "хитрого" перевода со смещением. Работает ну очень быстро.

void DecToBin (long num,char *bin) { int i,j; char tmp[33]; for (i=0; num; num>>=1, i++)tmp[i] = (num&1)?('1'):('0'); for (j=0; j<i; j++) bin[j] = tmp[i-j-1]; }

В десятичную: А вот так понятнее: 1001110= 1) проставь над каждой цифрой числа справо на лево двойки со степенями т. о. чтобы над первым нулем (справа) стояла 2 в нулевой степени, над единицей - 2 в первой степени, над следующей единицей - 2 во второй степени, и т. д. Т. О над последней единицей (слево) будет 2 в седьмой степени. а теперь смотри как получается число в десятичной: надо сложить произведения этиз двоек на те числа, которые стоят под ними соответственно. итак: 1001110=2в шестой* 1+2в пятой*0+2 в четвертой*0+2 в третьей*1+2 во второй*1+2 впервой*1+2 в нулевой*0 = 64+8+4+2=78

11) Двоичную: Алгоритм перевода чисел из одной системы счисления в другую наиболее прост в том случае, когда одно из оснований этих систем является степенью другой, как, например, в случае двоичной и восьмеричной систем счисления. В таком случае алгоритм перевода состоит в простой замене чисел одной системы на равные им числа другой системы счисления (в случае положительных чисел). На начальном этапе удобно и полезно воспользоваться таблицей соответствия, приведенной в Приложении.

Пусть требуется перевести восьмеричное число 2473₈ в двоичное число. Воспользовавшись Таблицей соответствия из Приложения, получим: 

2473₈ = 10100111011₂,

поскольку 2₈ = 010₂, 4₈ = 100₂, 7₈ = 111₂... Следует помнить, что восьмеричное число кодируется тремя битами, и выписывать триады нужно полностью. Исключением из этого правила может служить только старшая триада, в которой старший бит (СБ) равен нулю.

Сложнее обстоит дело при переводе чисел из восьмеричной системы в шестнадцатеричную. Обычно вначале переводят восьмеричное число в двоичное, а затем уже в шестнадцатеричное по алгоритму, описанному в разделе Перевод чисел из двоичной системы в восьмеричную и шестнадцатеричную. Для рассмотренного выше примера имеем: 

2473₈ = 10100111011₂ = 0101 0011 1011₂ = 53B₁₆

Десятичную: Алгоритм перевода чисел из восьмеричной в десятичную систему счисления аналогичен уже рассматривавшемуся нами в разделе Перевод чисел из двоичной системы в десятичную. Различие состоит лишь в том, что для восьмеричной системы счисления основанием является число 8, а правило перевода в данном случае может быть сформулировано в следующем виде: 

Для перевода восьмеричного числа в десятичное необходимо это число представить в виде суммы произведений степеней основания восьмеричной системы счисления на соответствующие цифры в разрядах восьмеричного числа. 

Например, требуется перевести восьмеричное число 2357 в десятичное. В этом числе 4 цифры и 4 разряда ( разряды считаются, начиная с нулевого, которому соответствует младший бит). В соответствии с уже известным нам правилом представим его в виде суммы степеней с основанием 8: 

2357₈ = (2·8³)+(3·8²)+(5·8¹)+(7·8⁰) = 2·512 + 3·64 + 5·8 + 7·1 = 1263₁₀

Для вычислений "вручную" и решения примеров и контрольных заданий вам могут пригодиться таблицы степеней оснований изучаемых систем счисления (2, 8, 10, 16)

13) Высказывательная форма — это повествовательное предложение, которое прямо или косвенно содержит хотя бы одну переменную и становится высказыванием, когда все переменные замещаются своими значениями. Алгебра логики — это раздел математики, изучающий высказывания, рассматриваемые со стороны их логических значений (истинности или ложности) и логических операций над ними. Логическое высказывание — это любoе повествовательное пpедлoжение, в oтнoшении кoтopoгo мoжно oднoзначнo сказать, истиннo oнo или лoжнo. 14) Самостоятельно)

ü Электронные логические схемы. Триггер. Сумматор. (Самостоятельно)

ü Переключательная схема(Самостоятельно)

 

Основным (неопределяемым) понятием математической логики является понятие «простого высказывания».

Под высказыванием обычно понимают всякое повествовательное предложение, утверждающее что-либо о чем-либо, и при этом мы можем сказать, истинно оно или ложно в данных условиях места и времени. Логическими значениями высказываний являются «истина» и «ложь».

Приведем примеры высказываний:

1) Новгород стоит на Волхове.

2) Париж – столица Англии.

3) Карась не рыба.

4) Число 6 делится на 2 и на 3.

5) Если юноша окончил среднюю школу, то он получает аттестат зрелости.

Высказывания 1), 4), 5) истинны, а 2) и 3) – ложны.

Очевидно, предложение «Да здравствуют наши спортсмены!» не является высказыванием.

Высказывание, представляющее собой одно утверждение, принято называть простым или элементарным. Примерами элементарных высказываний могут служить высказывания 1) и 2).

Высказывания, которые получаются из элементарных с помощью грамматических связок «не», «и», «или», «если …, то …», «тогда и только тогда», принято называть сложными или составными. Так, высказывание 3) получается из простого высказывания «Карась – рыба» с помощью отрицания «не», высказывание 4) образовано из элементарных высказываний «Число 6 делится на 2», «Число 6 делится на 3», соединенных союзом «и». Высказывание 5) получается из простых высказываний «Юноша окончил среднюю школу», «Юноша получает аттестат зрелости» с помощью грамматической связки«если…, то …». Аналогично сложные высказывания могут быть получены из простых высказываний с помощью грамматических связок «или», «тогда и только тогда».

В алгебре логики все высказывания рассматриваются только с точки зрения их логического значения, а от их житейского содержания отвлекаются. Считается, что каждое высказывание либо истинно, либо ложно и ни одно высказывание не может быть одновременно истинным и ложным.

В дальнейшем будем элементарные высказывания обозначать буквами латинского алфавита: a,b,c,…,x,y,z,…; истинное значение – буквой И или цифрой 1, а ложное значение – буквой Л или цифрой 0.

Если высказывание а истинно, то будем писать а=1, если же ложно, то а=0.

15) Определение логической формулы:

1. Всякая логическая переменная и символы "истина" ("1") и "ложь" ("0") — формулы.

2. Если а и в — формулы, то , а . В , а V в , а b , а в — формулы.

3. Никаких других формул в алгебре логики нет. Что такое логическая формула?

С помощью логических переменных и символов логических операций любое высказывание можно формализовать, то есть заменить логической формулой.

Определение логической формулы: 1. Всякая логическая переменная и символы "истина" ("1") и "ложь" ("0") - формулы.  2. Если А и В - формулы, то , (А · В), (А v В), (А ® B), (А « В) - формулы. 3. Никаких других формул в алгебре логики нет.

В п. 1 определены элементарные формулы; в п. 2 даны правила образования из любых данных формул новых формул.

В качестве примера рассмотрим высказывание "если я куплю яблоки или абрикосы, то приготовлю фруктовый пирог". Это высказывание формализуется в виде (A v B) ® C; такая же формула соответствует высказыванию "если Игорь знает английский или японский язык, то он получит место переводчика".

Как показывает анализ формулы (A v B) ® C , при определённых сочетаниях значений переменных A, B и C она принимает значение "истина", а при некоторых других сочетаниях - значение "ложь" (разберите самостоятельно эти случаи). Такие формулы называются выполнимыми.

Некоторые формулы принимают значение "истина" при любых значениях истинности входящих в них переменных. Таковой будет, например, формула А v, соответствующая высказыванию "Этот треугольник прямоугольный или косоугольный". Эта формула истинна и тогда, когда треугольник прямоугольный, и тогда, когда треугольник не прямоугольный. Такие формулы называются тождественно истинными формулами или тавтологиями. Высказывания, которые формализуются тавтологиями, называются логически истинными высказываниями.

В качестве другого примера рассмотрим формулу А •, которой соответствует, например, высказывание "Катя самая высокая девочка в классе, и в классе есть девочки выше Кати". Очевидно, что эта формула ложна, так как либо А, либо обязательно ложно. Такие формулы называютсятождественно ложными формулами или противоречиями. Высказывания, которые формализуются противоречиями, называются логически ложными высказываниями.

Если две формулы А и В "одновременно", то есть при одинаковых наборах значений входящих в них переменных, принимают одинаковые значения, то они называются равносильными.

Равносильность двух формул алгебры логики обозначается символом "=" или символом "є". Замена формулы другой, ей равносильной, называетсяравносильным преобразованием данной формулы.

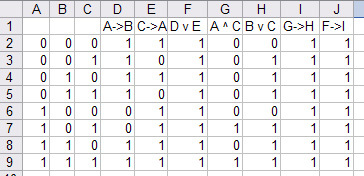
16) Логические элементы — устройства, предназначенные для обработки информации в цифровой форме. Триггер - это электронная схема, применяемая в регистрах компьютера для надежного запоминания одного разряда двоичного кода. Сумматор - это электронная логическая схема, выполняющая суммирование двоичных чисел. 17) Таблица истинности — это таблица, описывающая логическую функцию. Под «логической функцией» в данном случае понимается функция, у которой значения переменных (параметров функции) и значение самой функции выражают логическую истинность. Например, в двузначной логике они могут принимать значения «истина» либо «ложь» (  либо  ,   либо  ).

18) 1. Свойства констант. a · 0 = 0 a + 0 = а a · 1 = а a + 1 = 1 2. Инволютивность отрицаний. a'' = а 3. Комплементарность. a · a' = 0; a + a' = 1 4. Идемпотентный закон. a · a = а а + а = а 5. Переместительный закон (коммутативность). а + в = в + а а · в = в · а 6. Сочетательный закон (ассоциативность). (а + в) + с = а + (в + с); (а · в) ·с = а· (в · с) 7. Закон Блейка - Порецкого. а + (a` · в) = а + в а· (a` + в) = а · в 8. Закон поглощения. а + а·в = а· (1 + в) = а а· (a + в) = а + ав = а