188. Есептеңіз
A) [+]1/3.
B) 1.
C) –1/3.
D) 2/3.
E) –2/3.
189. Есептеңіз
A)
[+]
.
B)
.
C)
.
D)
E)
190.
Интегралды
есептеңіз
A)
B)
C)
D)
E)
[+]
191.Найти
площадь
фигуры, ограниченной линиями
A)
[+]
.
B)
.
C)
D)
E)
192.Найти
площадь
фигуры, ограниченной линиями
A) 1.
B) [+] 2.
C) –1.
D) 0.
E) –2.
193.
Найти
площадь
фигуры, ограниченной линиями
A) 2
B) [+] 4
C) 5
D) 1
E) 0
194. Есептеңіз
A) 21.
B) [+] 10,5.
C) 0,5.
D) 20.
E) 0,1
195.
Интегралды
есептеңіз
A)
.
B)
.
C)
[+]
.
D)
.
E) .
196. Есептеңіз
A) 5/3.
B) 0.
C) –8/3.
D) [+] 8/3.
E) 1/3.
197.
Интегралды
есептеңіз
A)
[+]
B)
C)
D)
E)
198.
Интегралды
есептеңіз
A)
B)
C)
[+]
D)
E)
199.
Вычислить площадь фигуры, ограниченной
линиями
A) 2.
B) 3.
C) [+] 3/2.
D) 5.
E) 6.
200.
Вычислить площадь фигуры, ограниченной
линиями
A) 2
B) 4.
C) 6.
D) [+] 8.
E) 1.
201.
Найти
площадь
фигуры, ограниченной линиями
A) [+]1.
B) 2.
C) –1.
D) 0.
E) -2.
202.
Интегралды
есептеңіз
A) .
B) .
C)
D) .
E)
[+]
.
203.
Интегралды
есептеңіз
A)
[+]
.
B)
.
C)
.
D)
.
E)
.
204.
Есептеңіз
A)
B)
C)
D)
E)
[+]
205.
Интегралды
есептеңіз
A)
B)
[+]
C)
D)
E)
206.
Есептеңіз
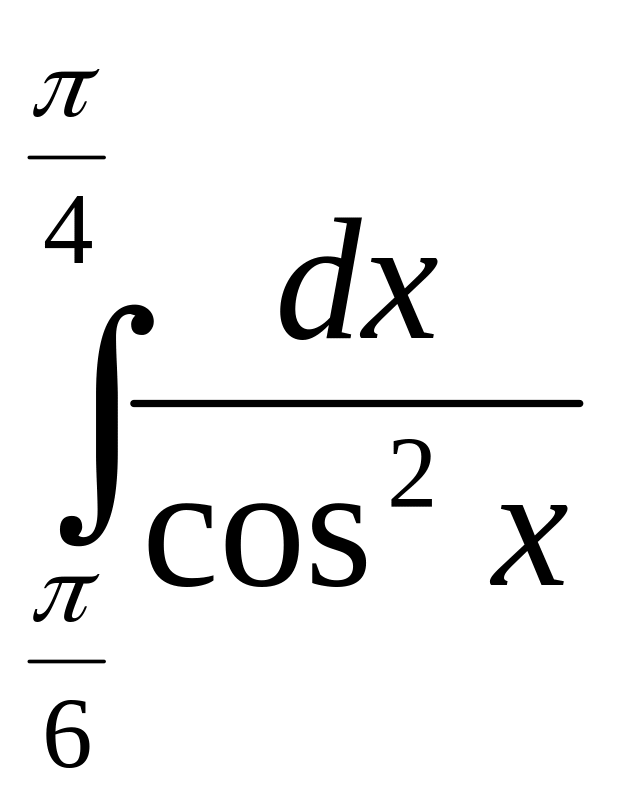
A)
[+]
.
B)
.
C)
.
D) -
E)
1 +
.
207.
Есептеңіз
A)
B)
[+]
C)
D)
E)
208.
Есептеңіз
A) 5
B) 3/2.
C) [+]5/2.
D) 0.
E) 2.
209.
Интегралды
есептеңіз
A)
B)
[+]
C)
D)
E)
210. Неопределенный интеграл, это
A)
[+] совокупность всех первообразных от
функции
B) первообразная от функции
C) производная от функции
D) дифференциал от функции
E) C,D.
211. Интегрирование посредством замены
A)
где
B)
[+]
где
C)
где
D)
где
E) C, D.
212.Формула интегрирования по частям:
A)
где
дифференцируемые функции.
B)
где
дифференцируемые функции.
C)
[+]
где
дифференцируемые функции.
D)
где
дифференцируемые функции.
E)
где
дифференцируемые функции.
213.
A)
B)
C)
D)
[+]
E)
214. Функция имеет максимум при , если для всех значений и достаточно близких к , выполняется неравенство:
A) [+]
B)
C)
D)
E)
215. Формула Ньютона-Лейбница
A)
[+]
.
B)
.
C)
.
D)
.
E)
.
216. Есептеңіз
A)
.
B) [+] 0.
C)
.
D)
.
E) 1.
217. Продолжить следующее свойство определенного интеграла.
При перестановки пределов интегрирования:
A) интеграл удваивается.
B) интеграл не изменяется.
C) [+] изменяется знак интеграла.
D) интеграл будет равен нулю.
E) A,C.
218.
Если функция
дифференцируема
и возрастает на промежутке
,
то при всех
A) ее производная отрицательна.
B) [+] ее производная положительна.
C) ее производная равна нулю.
D) не существует производной
E) A, C.
219.
Если функция
дифференцируема и убывает на промежутке
,
то при всех
:
A) [+] ее производная отрицательна.
B) ее производная положительна.
C) ее производная равна нулю.
D) не существует производной .
E) A,C.
220.Если
тело образуется при вращении вокруг
оси
,
то обьем этого тела определяется
формулой:
A)
B)
[+]
C)
D)
E)
221. Функция называется убывающей на промежутке , если:
A) на этом промежутке принимает только положительные значения.
B)
большему значению
соответствует большее значение
.
C) [+]большему значению соответствует меньшее значение .
D) на этом промежутке принимает отрицательные значения.
E) A, C.
E)[+]
222.
Интегралды есептеңіз
A)
B)[+]
C)
D)
E)
223.
Интегралды
есептеңіз
A)
.
B)
[+]
C)
D)
E)
224. Какие из следующих формул верны:
1)
,
2)
,
3)
,
4)
,
5)
.
A) 1, 2, 3, 4, 5.
B) 1, 2.
C) 2, 4.
D) [+]2, 3, 5.
E) 1, 4, 5.
225. Функция называется возрастающей на промежутке , если:
A) на этом промежутке принимает только положительные значения.
B) [+] большему значению соответствует большее значение .
C) большему значению соответствует меньшее значение .
D) на этом промежутке принимает отрицательные значения.
E) A, C.
226. Какое из указанных свойств определенного интеграла называют теоремой о среднем
A)
B)
C)
D)
[+]
,
если
непрерывна
на отрезке
E)
,
если
227.
Интегралды
есептеңіз
A)
B)
C)
[+]
D)
E)
