1. теңдеулер жүйесінің анықтауышы –25-ке тең екенін біле отырып, х₁ -ді табу керек:

A) –1.

B) 0.

C) 1.

D) 2.

E) [+] 3

2. Сызықтық теңдеулер жүйесі үйлесімді, егер:

A) шешімі болмаса

B) [+] кем дегенде бір шешімі болса

C) шешімдері бос жиын

D) түріндегі теңдеу болса

E) барлық жауаптар дұрыс

3. А - сызықтық теңдеулер жүйесінің негізгі матрицасы, В - кеңейтілген матрица болсын. Сызықтық теңдеулер жүйесі үйлесімді, егер

A) rang A ≠ rang B.

B) rang A < rang B.

C) [+]rang A = rang B.

D) барлық жауаптар дұрыс

E) Rang A> rang B.

4. Сызықтық теңдеулер жүйесін шешіңіз

A) [+](-4; -1).

B) (0; 3).

C) (1; -4).

D) (4; 1).

E) (-4; 1).

5.  -ның қандай мәнінде, сызықтық теңдеулер жүйесінің шешімі шексіз көп:

A) [+]1

B) –1.

C) 0.

D) 1.

E) 2.

6. Сызықтық теңдеулер жүйесін шешіңіз

A) (1,1,0).

B) (-1,1,-1).

C) (-1,1,2).

D) (2,1,0).

E) [+](1,1,1).

7. Теңдеулер жүйесінің анықтауышын табыңыз:

A) =8.

B) [+] =6.

C) =-8.

D) =4.

E) =1.

8. Теңдеудің түбірлерін табыңыз = 0:

A) [+]

B)

C)

D)

E) Түбірлері жоқ

9. Анықтауышты есептеңіз

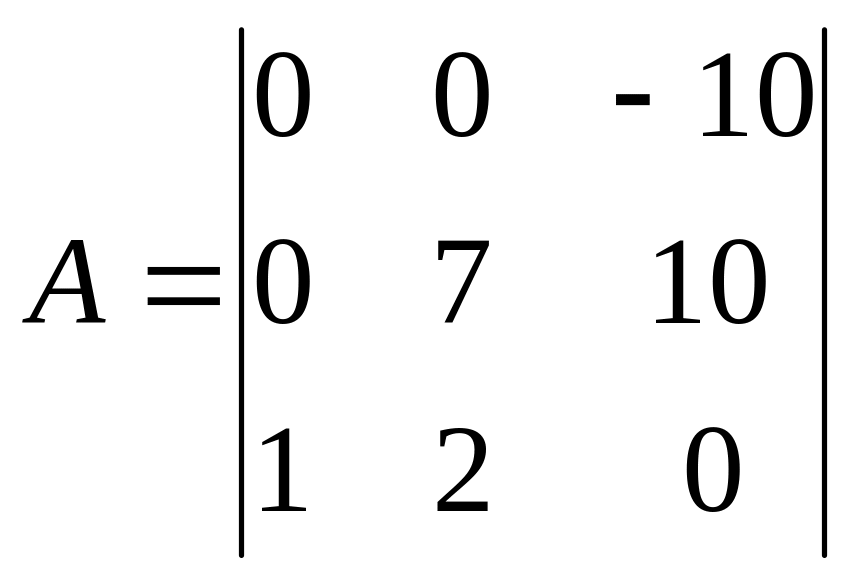
A) 25.

B) [+]70.

C) 80.

D) 50.

E) -70.

10. Анықтауышты есептеңіз

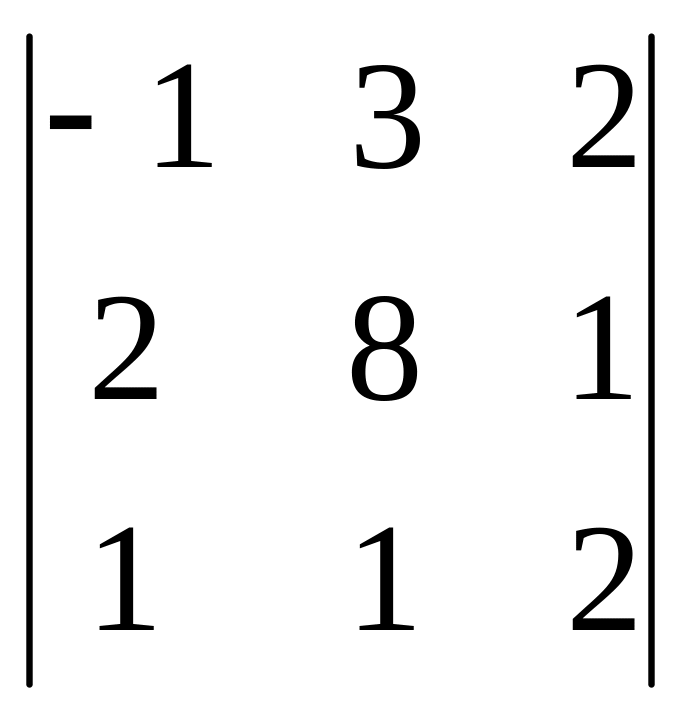
A) 3.

B) –36.

C) [+]–40.

D) –5.

E) -2.

11. Есептеңіз

A) 2sin α.

B) 2cos α.

C) 2sin α.

D) 2.

E) [+] 1

12. Анықтауышты есептеңіз А=

A) 24.

B) 40.

C) [+] -8.

D) -16.

E) 14.

13. Сызықтық теңдеулер жүйесін шешіңіз

A)

B)

C)

D)

E) [+]

14. Есептеңіз

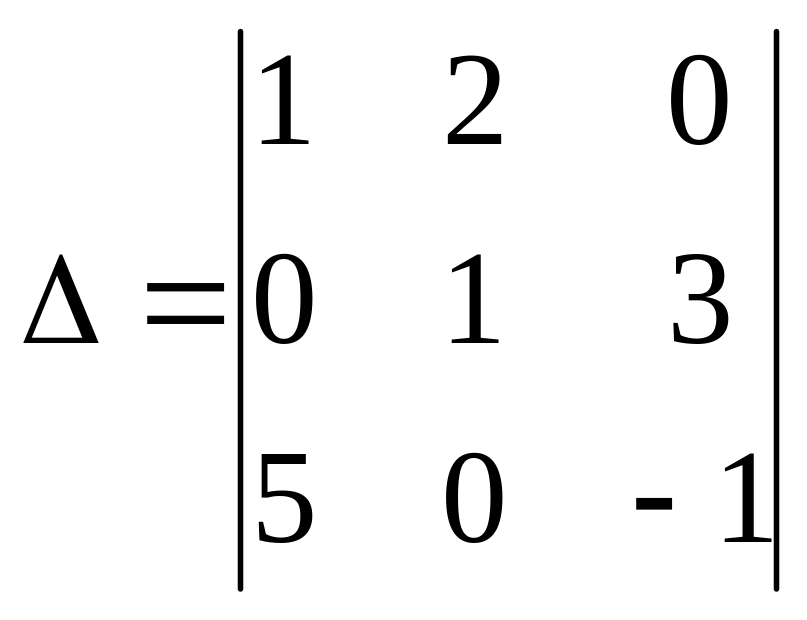
A) [+]29.

B) 22.

C) -31.

D) 31.

E) -29.

15. Сызықтық теңдеулер жүйесін шешіңіз:

A) [+](3;3)

B) (2;-2)

C) (5;3)

D) (4;1)

E) (2;1)

16. Теңдеудің түбірлерін табыңыз 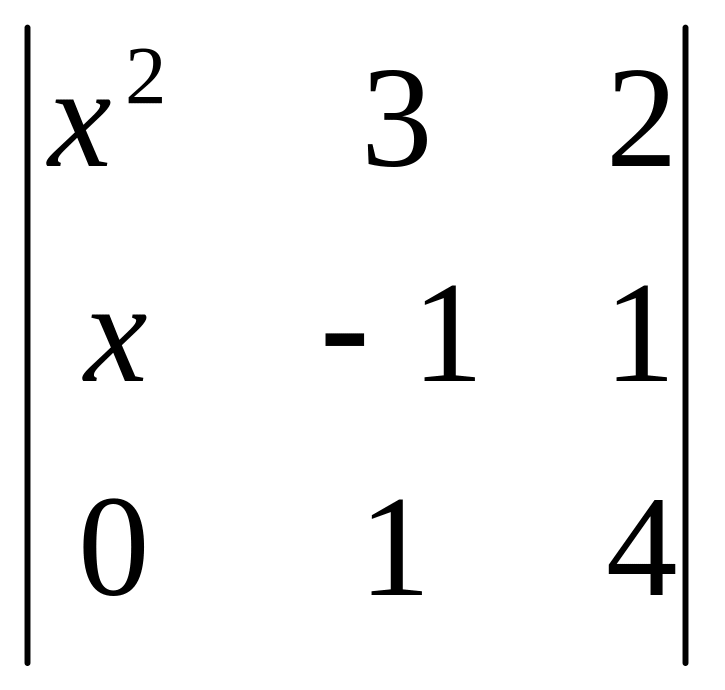=0

A) [+]

B)

C)

D)

E) Түбірлері жоқ.

17. Есептеңіз :

A) [+] 9.

B) 6.

C) -2

D) –9.

E) 4.

18. Есептеңіз :

A) [+] 1.

B) 3

C) –5.

D) 4.

E) 5.

19. Есептеңіз

A) [+] –8.

B) 40.

C) 45.

D) –40.

E) 9

20. Есептеңіз :

A) [+] –55.

B) 50.

C) 45.

D) 60.

E) –65.

21. Есептеңіз :

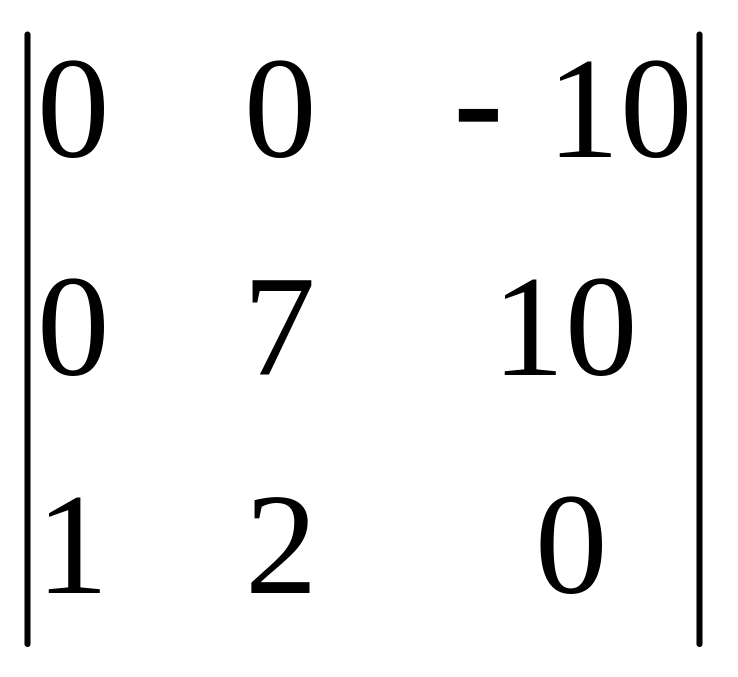A) [+] 70.

B) 20.

C) –35.

D) 60.

E) 65.

22. Есептеңіз

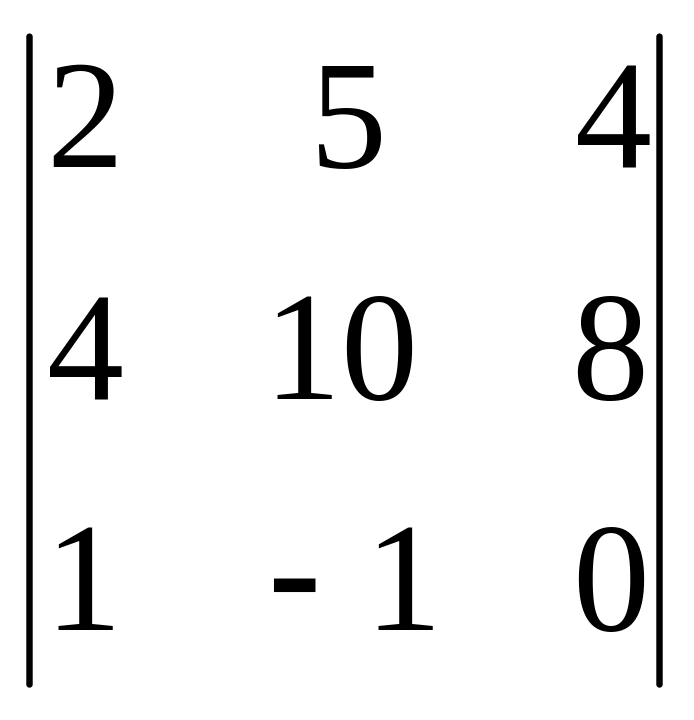
A) [+] 0.

B) 1.

C) –1.

D) 2.

E) –2.

23. Есептеңіз

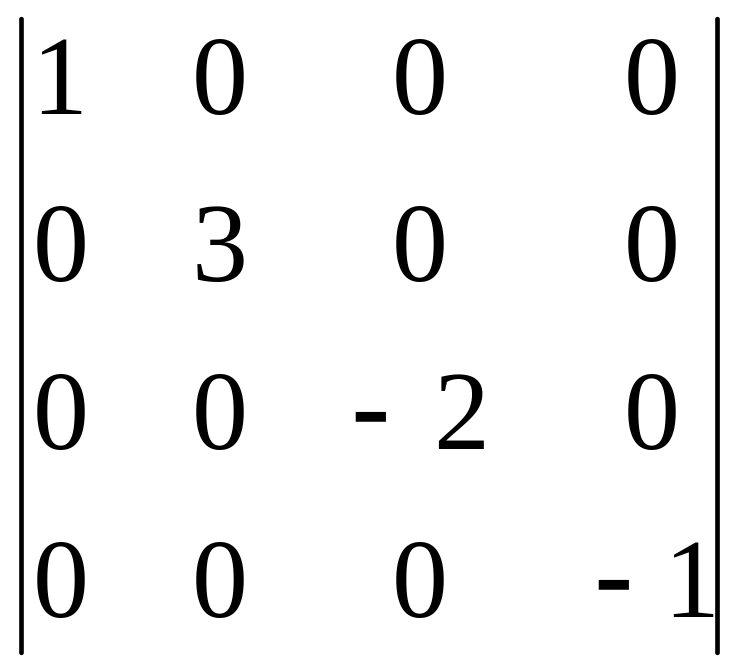
A) [+] 6.

B) 0.

C) 5.

D) –5.

E) –6.

24. Есептеңіз :

A) [+] 1.

B) .

C) .

D) –1.

E) 0.

25. Есептеңіз :

A) [+] .

B) .

C) .

D) .

E) 1.

26. Есептеңіз :

A) [+] 1.

B) .

C) .

D) 0.

E) –1.

27. анықтауышын есептеу формуласы:

A) [+] .

B) .

C) .

D) .

E) .

28. 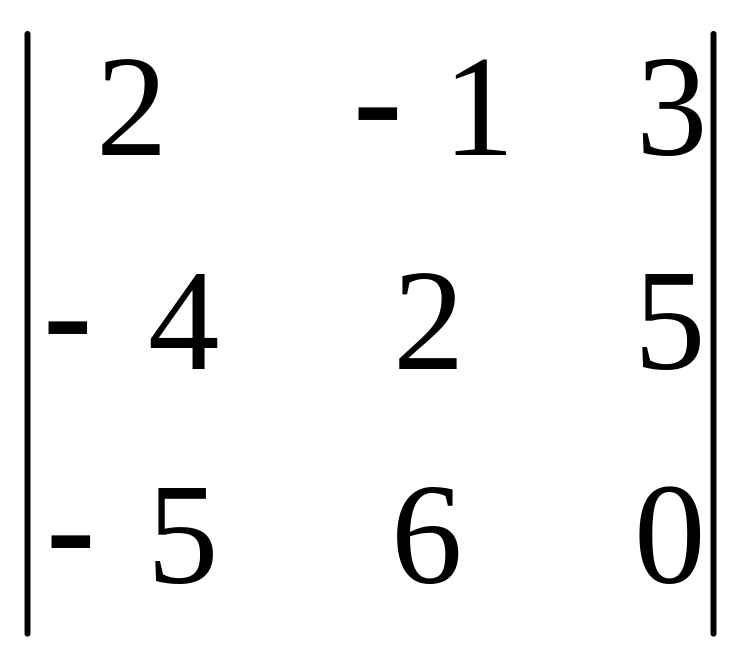анықтауышының алгебралық толықтауышын есептеңіз:

A) [+] –22.

B) –7.

C) 22.

D) 7.

E) 6.

29. Есептеңіз

A) [+] 30.

B) 28.

C) 34.

D) 32.

E) –30.

30.Үшінші ретті анықтауыштың элементінің минорына сәйкес өрнекті көрсетіңіз

A) [+] .

B) .

C) .

D) .

E) Дұрыс жауап жоқ.

31. Теңдеуді шешіңіз

A) Дұрыс жауап жоқ.

B) –2.

C) 2.

D) [+] .

E) .

32. 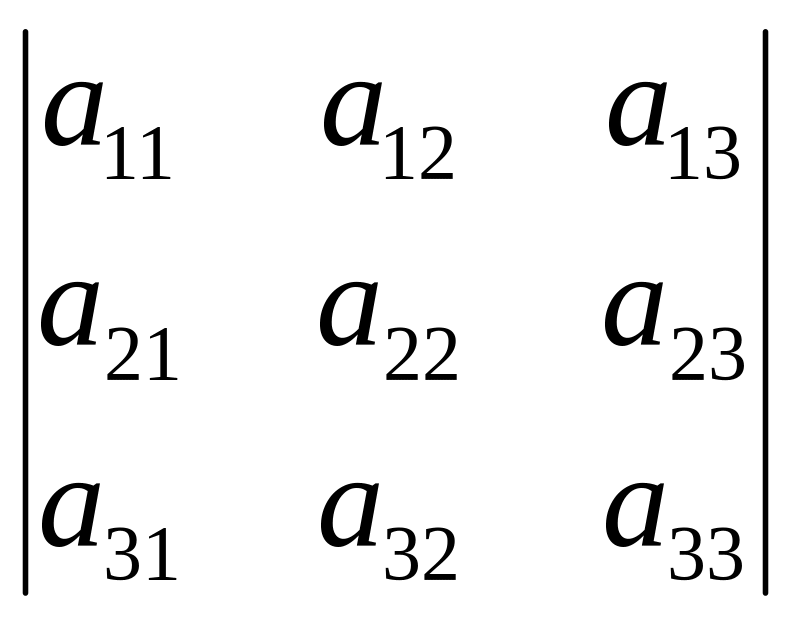анықтауышының алгебралық толықтауышы:

A) [+] .

B) .

C) .

D) .

E) .

33. Егер анықтауыштың екі параллель қатарларының орындарын ауыстырса, онда анықтауыш ...:

A) [+] (-1)-ге көбейтіледі

B) өзгермейді

C) 0-ге тең болады

D) 1-ге тең болады

E) кері шамаға өзгереді.

34. Егер анықтауыш екі қатары тең болса, онда анықтауыш ...:

A) [+]0-ге тең болады

B) ортақ көбейткішті анықтауыш таңбасының алдына шығаруға болады.

C) анықтауыш есептелмейді

D) (-1)-ге көбейтіледі

E) 1-ге тең болады

35. Анықтауыштың элементінің алгебралық толықтауышы ...:

A) [+] элементінің минорының -ге көбейтіндісі.

B) -ші жолы мен -ші бағанын сызып тастағаннан кейінгі анықтауыш

C) элементінің минорының бағаны.

D) элементінің минорының -ге көбейтіндісі.

E) Дұрыс жауап жоқ.

36. Есептеңіз .

A) –10.

B) 0.

C) 5.

D) –5.

E) [+]10

37. Егер анықтауыш кейбір қатарының барлық элементтері нолге тең болса, онда анықтауыш

A) [+]0-ге тең болады

B) ортақ көбейткішті анықтауыш таңбасының алдына шығаруға болады.

C) анықтауыш есептелмейді

D) (-1)-ге көбейтіледі

E) 1-ге тең болады

38. жазықтығының нормаль векторын анықтаңыз

A)

B)

C)

D) [+]

E) .

39. жазықтығына тиісті нүктесін анықтаңыз

A)

B)

C)

D) E) [+] .

4 0. -ның қандай мәнінде және түзулері параллель болады?

A) ;

B) [+] ;

C) ;

D) ;

E) .

41. Есептеңіз :

A) [+] 2 .

B) 0.

C) .

D) .

E) .

42. Есептеңіз :

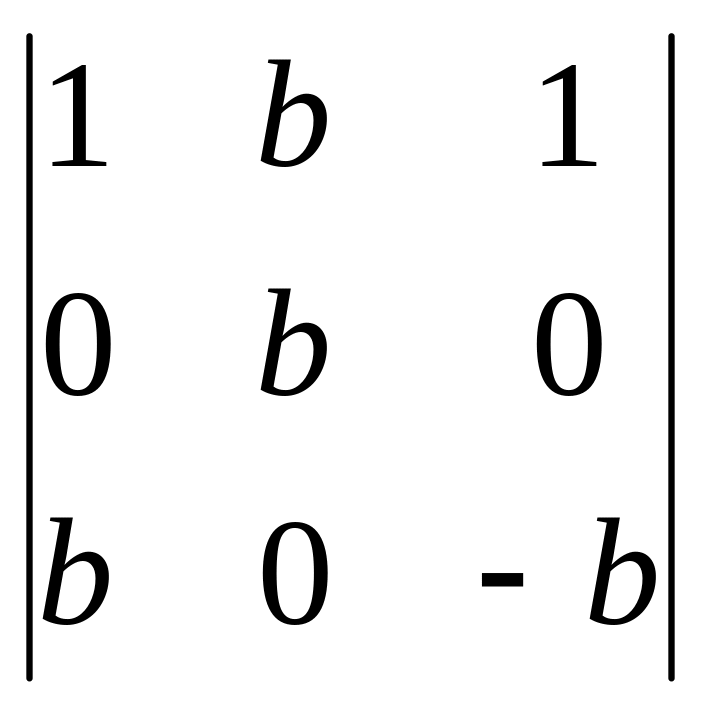A) [+] .

B) 0.

C) .

D) .

E) .

43. Есептеңіз :

A) [+] –11.

B) 1.

C) 10.

D) 12.

E) –1.

44. Есептеңіз :

A) [+] cos6x.

B) 1.

C) –1.

D) -cos6x.

E) sin6x.

45. Есептеңіз :

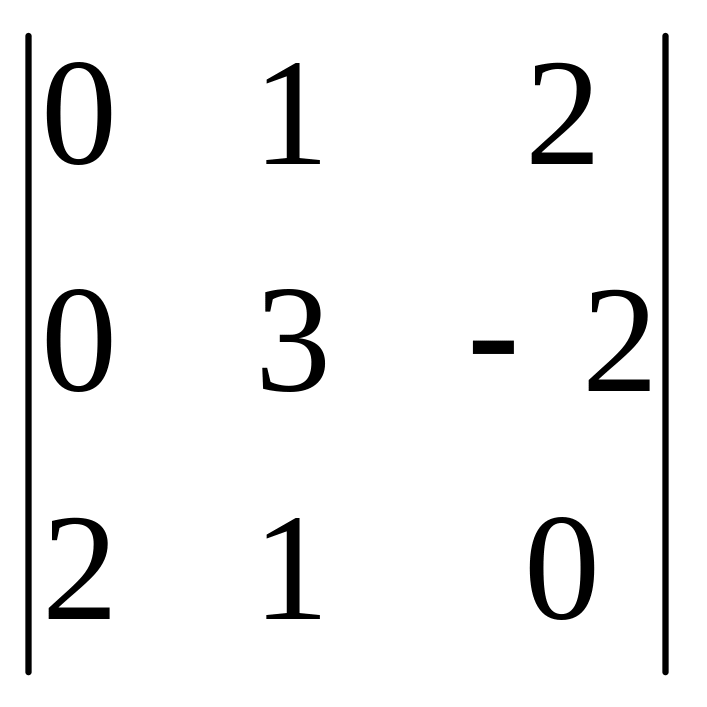A) [+] –16.

B) 8.

C) 16.

D) 7.

E) –6.

46. 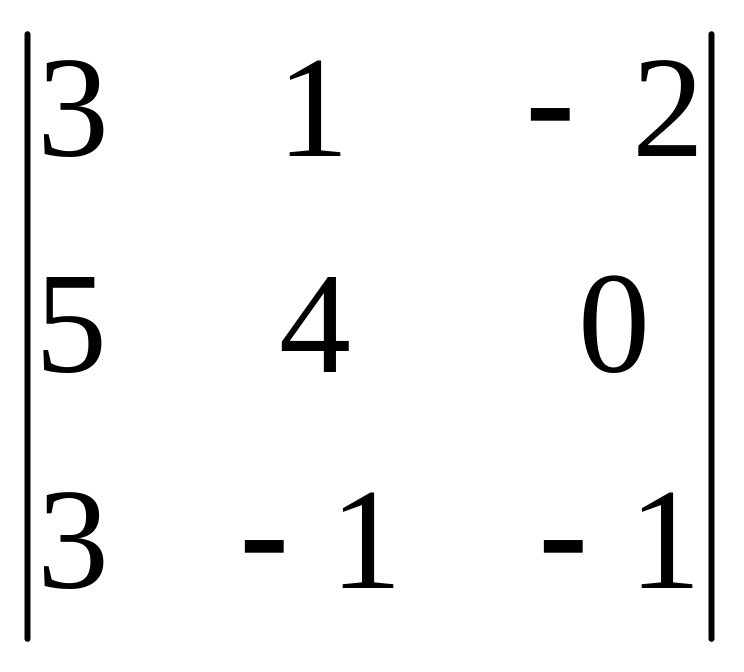анықтауышының минорын табыңыз

A) –6.

B) 0.

C) [+] 6.

D) 10.

E) –10.

47. 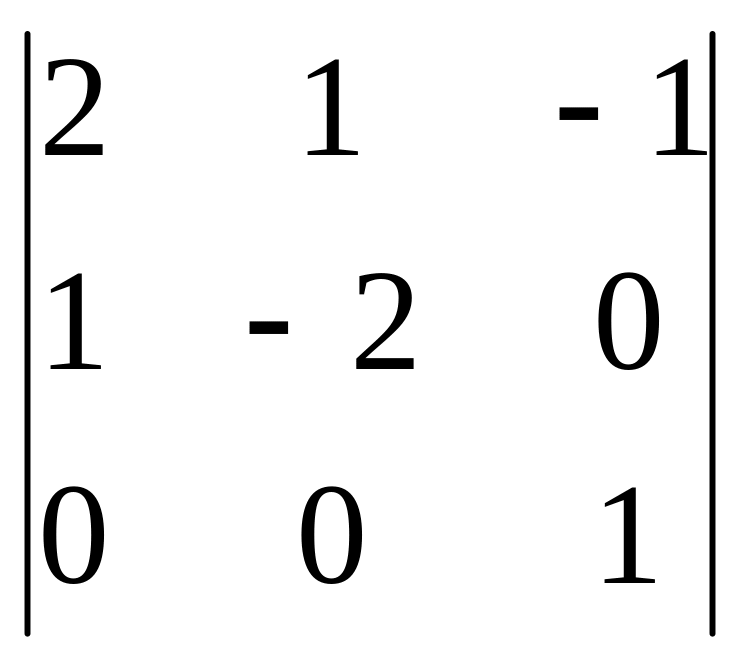анықтауышының минорын табыңыз

A) 1.

B) [+] –1.

C) 3.

D) –3.

E) 2.

48. Есептеңіз :

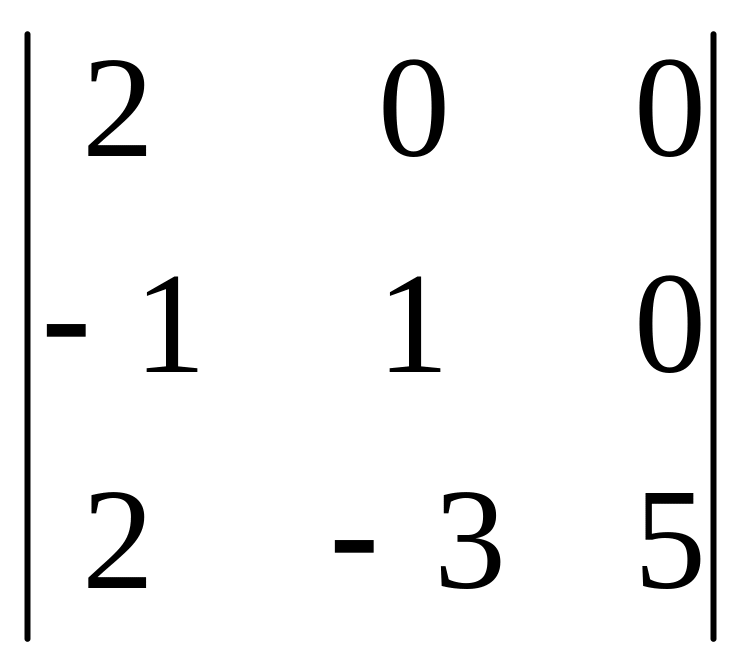A) [+] 10.

B) –10.

C) 3.

D) 7.

E) 6.

49. өлшемді матрицасына кері матрицасы бар болады, егер:

A) [+] .

B) .

C) .

D) .

E) .

50. берілген. матрицасының элементтерінің қосындысын табыңыз

A) [+] 2.

B) –6.

C) 6.

D) –2.

E) 4

51. Матрицаның рангы дегеніміз...:

A) [+] Нольге тең емес минорларының ең үлкен реті

B) бағандар саны

C) қатарлар саны

D) нольге тең емес минорларының саны

E) дұрыс жауап жоқ.

52. Бірлік матрицаны көрсетіңіз:

A) [+]

B)

C) .

D) .

E) .

53. Дұрыс теңдікті көрсетіңіз:

A) [+] .

B) .

C) .

D) .

E) дұрыс жауап жоқ.

54. Есептеңіз

A) [+] .

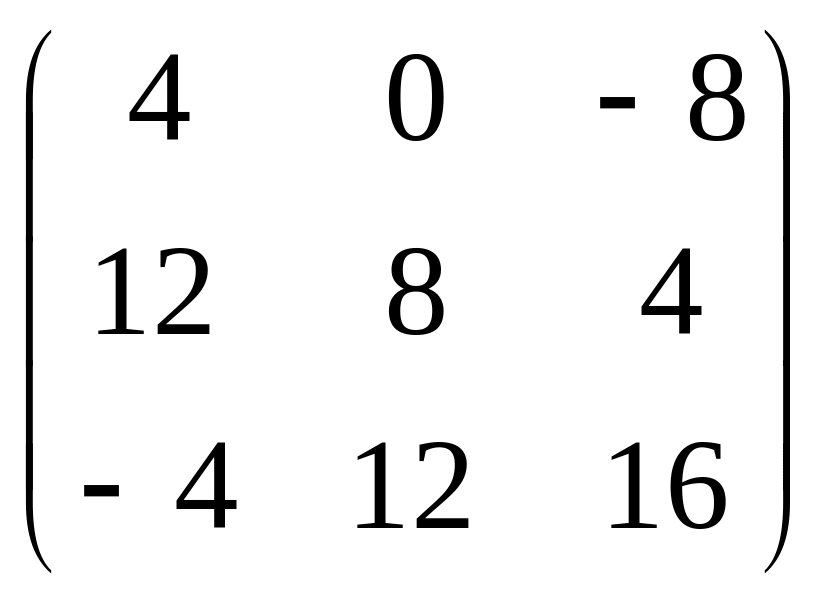B)

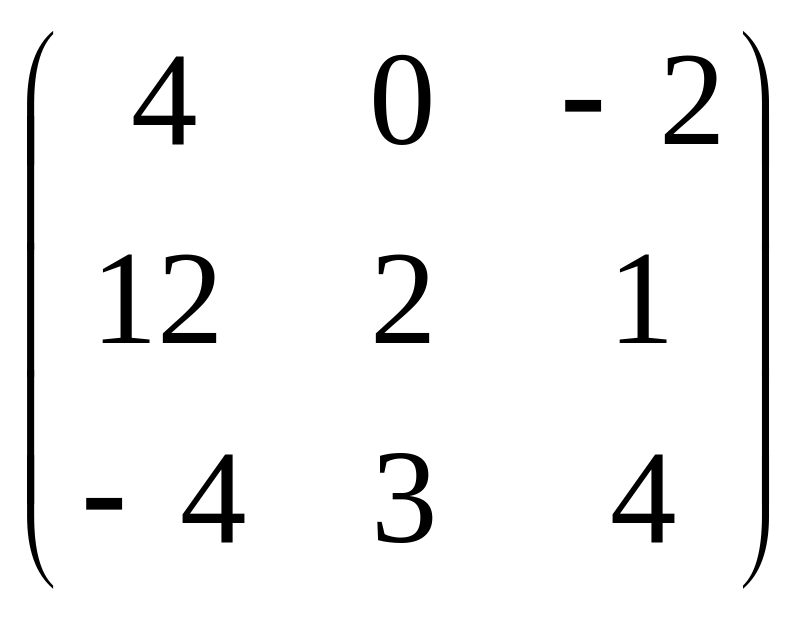
C) .

D) .

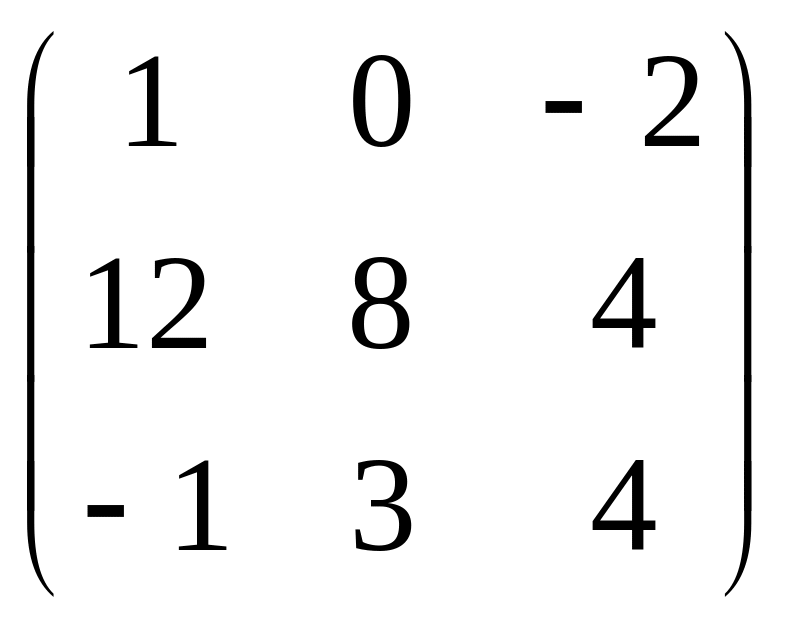E) .

55. 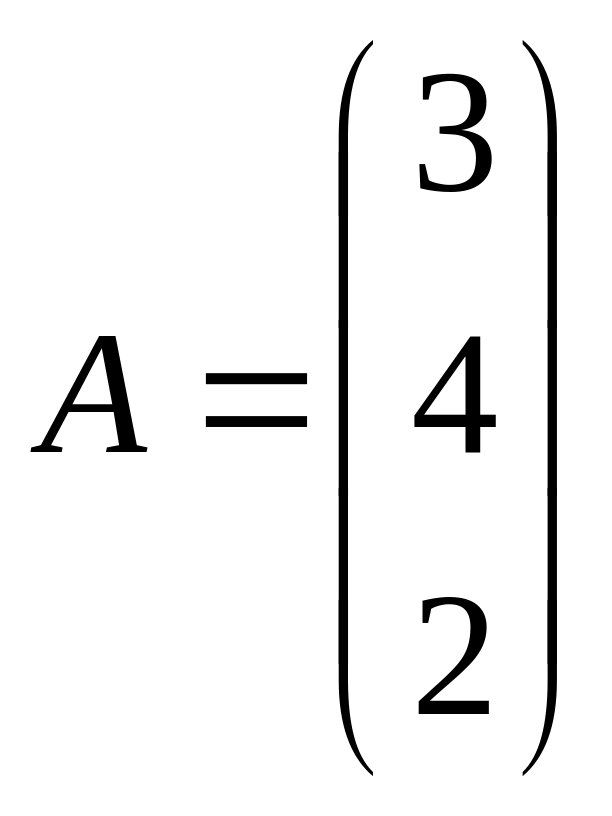және матрицалары берілген. табыңыз

A) көбейтуге болмайды

B) 13.

C) 29.

D) [+] .

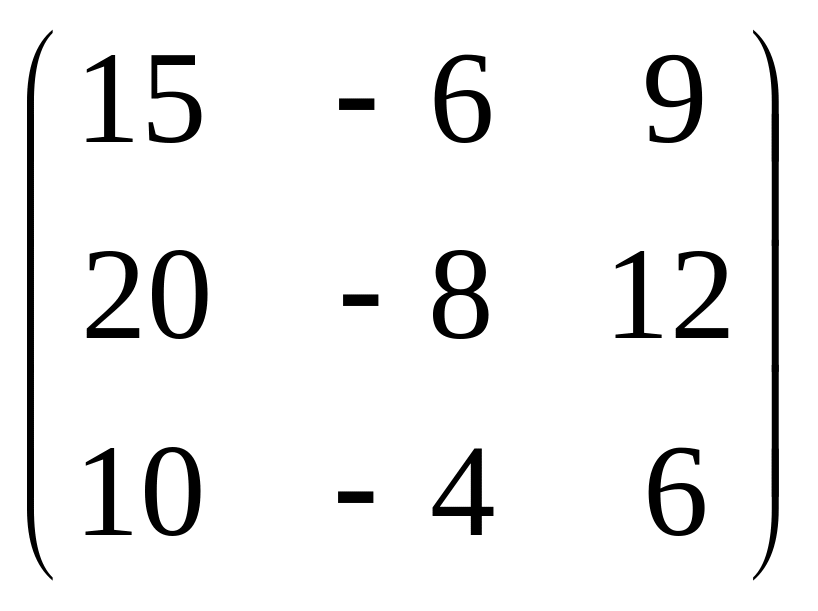E) .

56. матрицасы матрицасына көбейтілсін. С=АВ, ; болатындай матрицасы үшін орындалатын дұрыс өрнекті көрсетіңіз

A) .

B) .

C) .

D) [+] табылмайды

E) .

57. Есептеңіз , егер .

A) [+] табылмайды

B) .

C) .

D) .

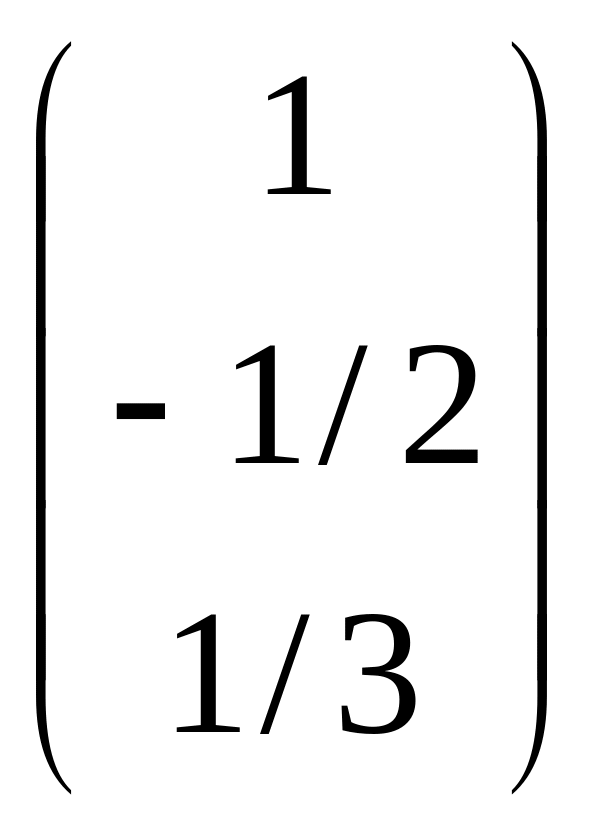E) .

58. Есептеңіз егер :

A) дұрыс жауап жоқ

B) .

C) .

D) [+] .

E) .

59. және матрицалары берілген. табыңыз

A) [+]табылмайды

B) .

C) .

D) .

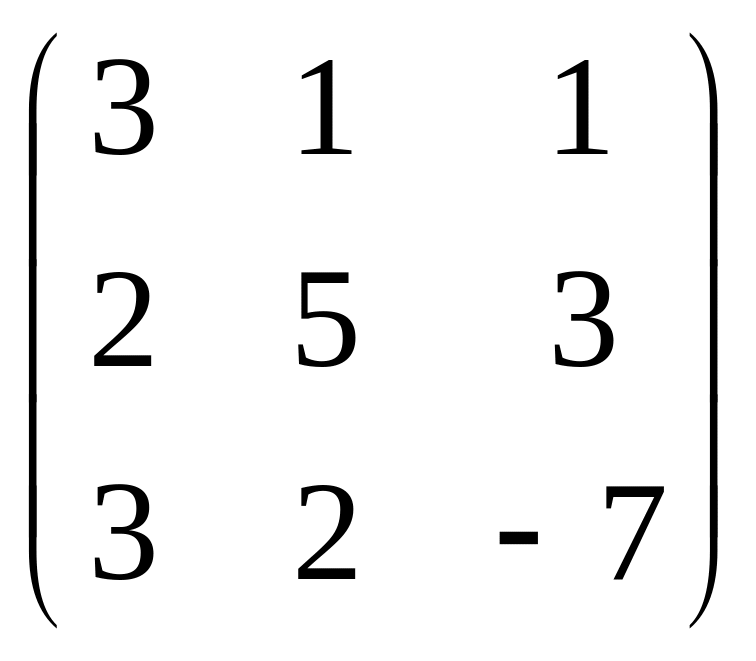E) дұрыс жауап жоқ

60. жүйесі анықталған және үйлесімді, егер:

A) [+] :

B) .

C) .

D) .

E) .

61. және векторларының скаляр көбейтіндісін табыңыз

A) 15;

B) [+]16;

C) 17;

D) 18;

E) 19.

62. жүйесінің шешімдерінің қосындысын табу (x+y+z) керек, егер y=1 болса:

A) [+] 2.

B) 0.

C) –4.

D) –2.

E) 4

63. теңдеулер жүйесінің шешімінің матрицалық түрі:

A) [+] .

B) .

C) .

D) .

E) дұрыс жауап жоқ

64. -ның қандай мәнінде жүйесінің шешімі нолдік болмайды?

A) [+] –3.

B) 2.

C) 5/2.

D) –2.

E) 3.

65. Жүйенің шешімдерін табыңыз .

A) [+]

B)

C)

D)

E)

66. Үйлесімді теңдеулер жүйесінің шешімі...:

A) [+] біреу немесе бірнеше

B) жалғыз

C) жоқ

D) шексіз көп

E) нолдік

67. Система линейных уравнений называется однородной, если:

A) [+]Bсе свободные члены равны нулю.

B) Хотя бы один из свободных членов системы отличен от нуля.

C) Хотя бы один из свободных членов равен нулю.

D) Все свободные члены не равны нулю.

E) Только один из свободных членов не равен нулю.

68. Система линейных уравнений называется определенной, если она...:

A) Совместна.

B) Совместна и имеет множество решений.

C) [+]Совместна и имеет единственное решение.

D) Несовместна.

E) Однородная.

69. -ның қандай мәнінде жүйесінің шешімі жалғыз?

A)

B) 0

C) 1

D)

E) [+] кез-келген

70. үйлесімсіз, егер:

A) .

B) .

C) .

D) [+] .

E) .

71. Жүйені шешіп, (2x+y)-ті табыңыз :

A) [+] 4.

B) –3.

C) 2.

D) –2.

E) 0.

72. -ның қандай мәнінде жүйесінің шешімі болмайды?

A) [+] –1.

B) 2.

C) 1.

D) –2.

E) 3.

73. -ның қандай мәнінде жүйесі анықталмаған?

A) [+] –12.

B) 3.

C) –3.

D) 12.

E) 4.

74. түзуіне перпендикуляр түзу:

A) ;

B) ;

C)

D) ;

E) [+] .

75. АВ кесіндісінің ортасының координаталарын табыңыз, егер А(3; 6), В(5; 2)

A) [+] (4; 4).

B) (3; 5).

C) (4; 5).

D) (2; 3).

E) (1; 2).

76. түзуіне тиісті нүкте:

A) [+] (2;-5).

B) (4;2).

C) (3;0).

D) (0;0).

E) (1;-1).

77. a=1; b=2 болатын гиперболаның теңдеуі:

A) [+] .

B) .

C) .

D) .

E) .

78. Түзудің бұрыштық коэффициенті арқылы жазылған теңдеуі:

A) [+] .

B) .

C) .

D) .

E) .

79. түзуіне перпендикуляр түзу :

A) [+]

B)

C)

D)

E)

80. Қай теңдеу шеңберді анықтайды?

A) [+] .

B) .

C) .

D) .

E) .

81. Екі нүкте арқылы өтетін түзу теңдеуі:

A) [+] .

B) .

C) .

D) .

E) .

82. эллипсіне тиісті нүктені анықтаңыз?

A) [+] (2; 1).

B) (0; 1).

C) (9; 5).

D) (3; 2).

E) (0; 9).

83. Егер нүкте осінде жатса оның ординатасы:

A) [+] 0.

B) 1.

C) x.

D) y.

E) .

84. және түзулерінің арасындағы бұрышты анықтайтын формула:

A) [+] .

B)

C) .

D) .

E) .

85. түзуіне параллель түзу

A) [+]

B)

С) .

D) .

E) .

86. түзуінің бұрыштық коэффициенті:

A) [+]

B)

C)

D)

E)

87. Түзудің кесінділік теңдеуі:

A) [+] .

B) .

C) .

D) .

E) .

88. a=4; b=3 болатын эллипстің теңдеуі:

A) [+] .

B) .

C) .

D) .

E) .

89. және түзулерінің өзара орналасуын анықтаңыз

A) [+] өзара перпендикуляр

B) параллель

C) сүйір бұрыш жасап қиылысады

D) беттеседі

E) доғал бұрыш жасап қиылысады

90. А(3; 6), В(3; 4) болса, АВ кесіндісінің ортасының координаталарын табыңыздар

A) (4; 4).

B) [+] (3; 5).

C) (4; 5).

D) (2; 3).

E) (1; 2).

91. А (2;1) нүктесінен түзуіне түсірілген перпендикулярдың ұзындығы:

A) [+] .

B) .

C) 3.

D) 5.

92. Түзулердің параллельдік белгісі:

A) [+]

B)

C)

D)

E)

93. түзуі осін қандай бұрышпен қияды?

A)[+]

B)

C)

D)

E)

94. Егер ax+by+c=0 жазықтықтағы түзуді анықтаса, онда

A) [+]

B)

C)

D)

E)

95. Егер А(-6; -2) және В(4;3) болса, АВ кесіндісін А нүктесінен бастап 1:4 қатынаста бөлетін С нүктесінің координаталарын табыңыз :

A) (-1; 0,5).

B) (5; 25).

C) [+] (-4; -1).

D) (1; -0,5).

E) (4; 1).

96. Егер А(-2; 0) және В(3;3) болса, АВ түзуіне тиісті ординаталар осіндегі нүктені табыңыз:

A) (0; 3/2).

B)[+] (0; 6/5).

C) (0; 3).

D) (0; 2).

E) (0; -2).

97. векторларының скаляр көбейтіндісінің координаталық формасы :

A) [+] .

B) .

C) .

D) .

E) .

98. Егер , онда векторының координаталары:

A) [+] .

B) .

C) .

D) .

E) .

99. Егер болса, онда шартын қанағаттандыратын векторлары:

A) [+] бағыттас

B) қарама-қарсы бағытталған

C) перпендикуляр

D) әртүрлі бағытталған

E) тең

100. Егер А (-2; 0), С (4; 2), АС нүктелерінің ара қашықтығы:

A) 40.

B) [+] .

C) .

D) 20.

E) 30.

101. А (2; 3) нүктесінен түзуіне дейінгі ара қашықтық:

A) 3.

B) 2,5.

C) 3,5.

D) 2,8.

E) [+]1,6

102. А (-3; 4) нүктесінен осіне дейінгі ара қашықтық:

A) -3.

B) [+] 4.

C) 25.

D) 7.

E) 1.

103. түзуінің кесінділік теңдеуін жазыңыз.

A) = 1.

B) = 1.

C) [+] = 1.

D) = 1.

E) .

104. түзуіне тиісті нүкте:

A) (2; 1).

B) (2; 3).

C) [+] (2; 2).

D) (-2; -2).

E) (-2; 2).

105. Екі вектор өзара тең,егер:

A) модулдері тең болса

B) коллинеар болса

C) қарама-қарсы бағытталса

D) бағыттас болса

E) [+] модулдері тең, коллинеар және бағыттас болса

106. Егер және векторлары үшін шарты орындалса мұндағы , онда бұл векторлар:

A)[+] коллинеар

B) коллинеар емес

C) тең

D) бағыттас

E) тең және коллинеар

107. және векторларының арасындағы бұрыштың косинусы тең:

A) .

B) .

C) [+] .

D) .

E) .

108. және векторларының скаляр көбейтіндісі:

A) [+] .

B) .

C) .

D) .

E) .

109. Егер және векторлары үшін шарты орындалса, онда олар:

A) коллинеар

B) [+] перпендикуляр

C) тең

D) бағыттас

E) тең және коллинеар

110. Егер , болса, онда-ның қандай мәнінде , векторлары коллинеар болады?

A) 1

B)-1

C) -2,5

D) [+] 0

E) 2

111. және векторларының скаляр көбейтіндісін табыңыз:

A) 21

B) 19

C) [+]18

D) -12

E) 15

112. және нүктелері берілген. векторының координаталарын табыңыз:

A) (5;6)

B) [+](3;-4)

C) (-3;-4)

D) (-5;6)

E) (6;5)

113. және векторларының модулін табыңыз.

A) [+] .

B) .

C) .

D) .

E) .

114. Егер болса, онда векторының координаталарын табыңыз:

A) [+] .

B) .

C) .

D) .

E) .

115. А(6; 3; 4) және В(4;7;3) болса, векторының координаталарын табыңыз:

A) (2; 4; 1).

B) (-2; 4; 1).

C) (2; -4; -1).

D) (6; 10; -1).

E) [+](-2; 4; -1).