5. Сглаживние эмпирического распределения
Таблица 5.1.
Проверка гипотезы о нормальном распределении переменной Var1.
Рис. 1.1. Гистограмма и расчетная кривая нормального распределения для переменной Var1.
Таблица 5.2.
Проверка гипотезы о логарифмически нормальном распределении переменной Var1.
Рис. 2.1. Гистограмма и расчётная кривая логарифмически нормального распределения для переменной Var1.
Таблица 5.3.
Проверка гипотезы о прямоугольном распределении переменной Var1.
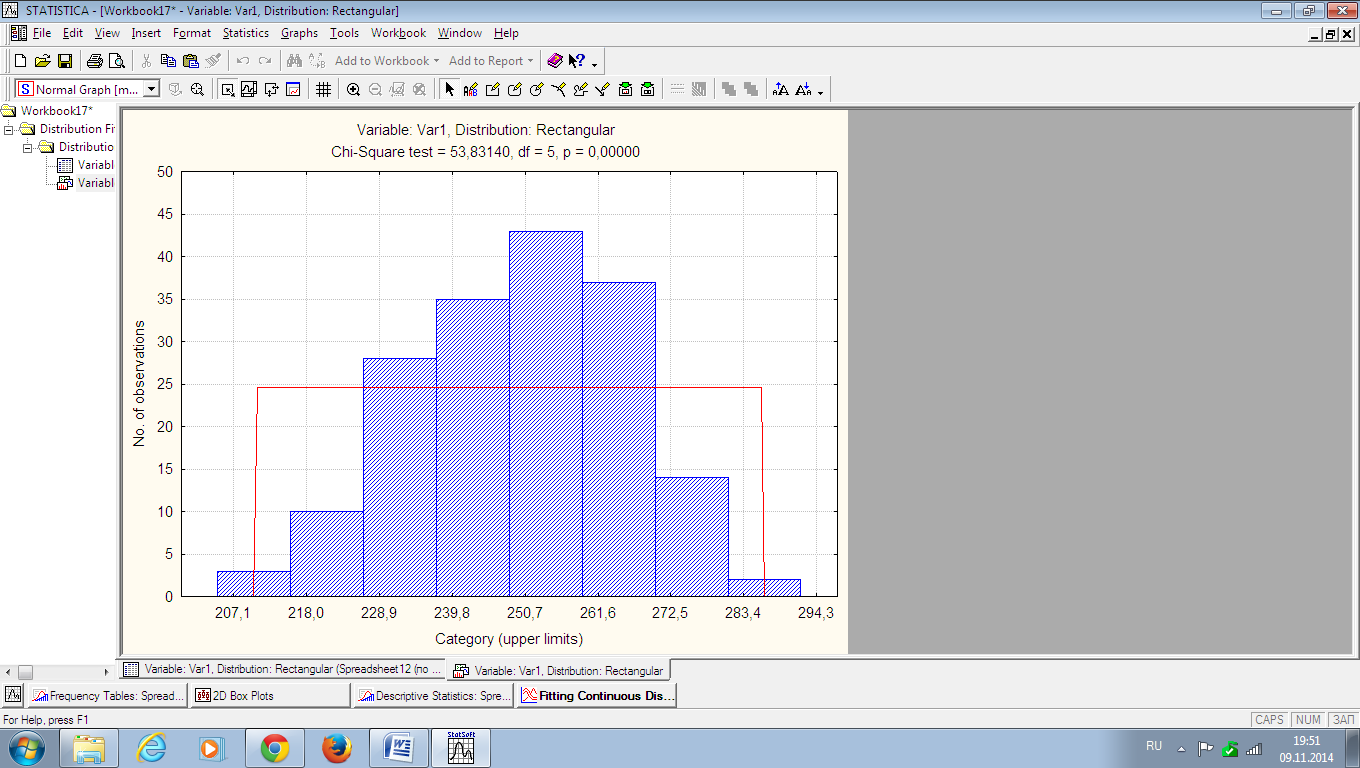
Рис. 3.1. Гистограмма и расчетная кривая прямоугольного распределения для переменной Var1.
Таблица 5.4.
Результаты решения задачи сглаживания
-
Тип распределения
Число степеней свободы
R
Расчетное значение критерия
Табличное значение критерия
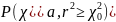
(расчетное значение уровня значимости)
1
Нормальное
5
381,45187
11,07
0,00000
2
Логнормальное
3
5,01112
7,815
0,17098
3
Прямоугольное
5
53,83140
11,07
0,00000
1. Так как
=
381,45187>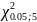
=
11,07
и
=
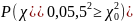0,00000 < α = 0,05,
то гипотеза о нормальном распределении переменной Var1 отвергается на 0,00000 уровне значимости.
2. Так как
=
5,01112 <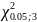
=
7,815 и
=
0,17098 > α = 0,05,
то гипотеза о логнормальном распределении переменной Var1 не противоречит статистическим данным.
3. Так как
= 53,83140 > = 11,07 и
= 0,00000 < α = 0,05,
то гипотеза о прямоугольном распределении переменной Var1 отвергается на 0,00000 уровне значимости.
Заключение
В результате в лабораторной работе проанализированы данные о распределении, были описаны и найдены статистические характеристики, выявлены закономерности распределения и определён её характер. В работе были проверены гипотезы соответствия эмпирического вариационного ряда нормальному, логнормальному и прямоугольному распределениям с помощью критерия 2 (критерий Пирсона).