Министерство образования и науки Российской Федерации
Государственное образовательное учреждение высшего
профессионального образования
«Санкт- Петербургский государственный
политехнический университет»
Инженерно-экономический институт
Кафедра « Предпринимательство и коммерция»
Лабораторная работа №1
по дисциплине « Статистика»
на тему « Анализ эмпирического распределения»
Выполнил: студент группы 33707/3
Сахно И.А.
Принял: ст. преподаватель
Куприенко Н.В.
Санкт- Петербург
2014
ОГЛАВЛЕНИЕ
ВВЕДЕНИЕ 4
1.ИСХОДНЫЕ ДАННЫЕ 5
2. РУЧНАЯ ОБРАБОТКА ДАННЫХ 7
3. ОБРАБОТКА ДАННЫХ В ПРОГРАММЕ STATISTICA 10
3.1. Табличное представление. 10
3.2. Графическое представление. 11
4. РАСЧЕТЫ ОСНОВНЫХ СТАТИСТИЧЕСКИХ ПОКАЗАТЕЛЕЙ 17
n – объем совокупности (Valid N). 17
5. СГЛАЖИВНИЕ ЭМПИРИЧЕСКОГО РАСПРЕДЕЛЕНИЯ 20
Введение
STATISTIKA – это универсальная интегрированная система, предназначенная для статистического анализа и визуализации данных, управления базами данных и разработки пользовательских приложений, содержащая широкий набор процедур анализа для применения в научных исследованиях, технике, бизнесе, а также специальные методы добычи данных.
Цель работы – приобретение практических навыков анализа распределения, в том числе в табличном и графическом виде.
Одним из важнейших направлений анализа исходных данных является статистический анализ распределений, поскольку позволяет получить обширную информацию об объекте исследования. Комплексный анализ рядов распределений включает расчёт характеристик центра распределения, его структуры, оценку степени вариации и дифференциации изучаемого признака, характеристику формы распределения.
1.Исходные данные
Таблица 1.1.
Исходные данные
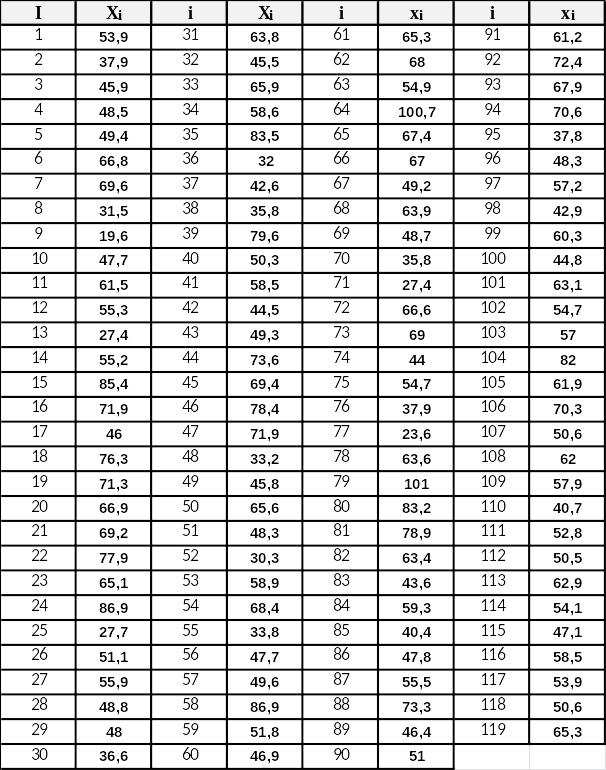
Таблица 1.2.
Исходные данные в порядке возрастания
2. Ручная обработка данных
Таблица 2.1.
Ручная обработка данных
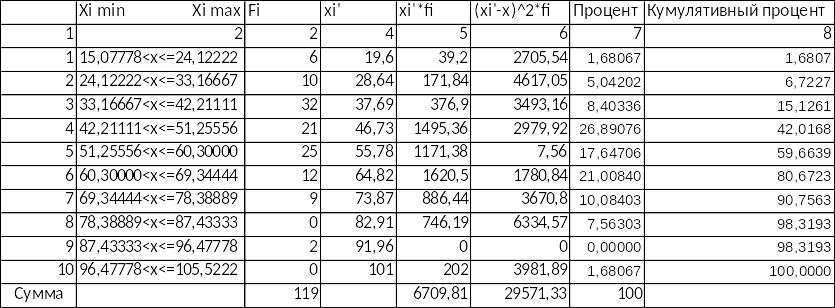
Взвешенная средняя арифметическая:
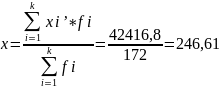
где
fi
– абсолютные частоты i-того интервала,
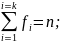
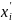– середина интервала i-того интервала.
Дисперсия:
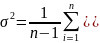
Медиана:
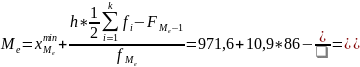
Мода:
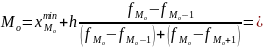
Где:
где
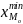– нижняя граница модального интервала;
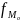– частота модального интервала;
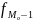– частота интервала перед модальным;
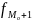– частота интервала после модального;
h – величина группировочного интервала.
Таблица 2.2.
Таблица
для расчета критерия
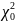вручную
-
№
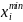
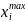
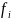
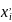
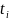
(t)
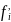
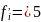
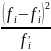
1
204,7500
215,6500
3
210,2
-14,756
0,0000
0
13,68
12,140
2
215,6500
226,550
10
221,1
-2,214
0,0347
3,957
3
226,5500
237,4500
28
232
-1,551
0,1200
13,68
4
237,4500
248,3500
35
242,9
-0,888
0,2709
30,89
30,89
0,547
5
248,3500
259,2500
43
253,8
-0,2256
0,3894
44,41
44,41
0,045
6
259,2500
270,1500
37
264,7
0,4373
0,3637
41,47
41,47
0,482
7
270,1500
281,0500
14
275,6
1,100
0,2179
24,85
24,85
4,737
8
281,0500
291,9500
2
286,5
1,763
0,0848
9,67
9,67
6,084
Сумма
172
168,94
168,92
24,035
d.f. (adjusted) – уточненное значение числа степеней свободы:
d. f. (r) = k – 2 – 1 = 8 – 2 – 1 = 5
k – число интервалов эмпирического распределения (вариационного ряда);
l – число параметров теоретического распределения, определяемых по опытным данным (например, в случае нормального закона распределения число оцениваемых по выборке параметров l = 2, математическое ожидание и дисперсия);
p – расчетный уровень значимости.
Так как x20 = 24,035 > 11,07, то гипотеза о распределении противоречит статистическим данным.