Оглавление

Задача № 1 3

Задача №2 3

Задача №3 4

Задача № 4 5

Задача № 5 6

Задача №6 7

Задача № 7 9

Задача №8 10

Задача № 9 11

Задача № 10 13

Задача № 11 13

Задача № 12 14

Задача № 13 15

Задача № 14 16

Задача № 15 16

Задача № 16 17

Задача № 17 18

Задача № 18 20

3.2.Определение оптимальных параметров экономической системы путем математического моделирования 26

Литература 28

Задача № 1

При перевозке 109 деталей, из которых 10 были забракованы, утеряна 1 стан­дартная деталь. Найти вероятность того, что наудачу извлеченная деталь (из оставшихся) окажется стандартной.

Решение

Находим по формуле классической вероятности вероятность выбора нестандартной детали:

Так как была утеряна стандартная деталь, их осталось 98. Отсюда:

Задача №2

На один ряд, состоящий из 13 мест, случайно садятся 13 учеников. Найти веро­ятность того, что 3 определенных ученика окажутся рядом.

Решение

По классическому определению вероятности, вероятность того, что три определённых лица окажутся рядом при случайном рассаживании на скамейку, равна отношению числа m способов расстановки десяти человек, при котором три определённых лица окажутся рядом, к общему числу разных расстановок десяти человек по десяти местам.

.

Общее число n различных расстановок, в которых имеет значение место конкретного человека, десяти человек по десяти местам равно числу размещений из 10 по 10:

Чтобы три ученика оказались рядом, их нужно рассаживать на три определённых места, а 10 остальных рассаживать в произвольном порядке на остальные 10 мест.

Пусть эти 3 ученика садятся на одно место, тогда у нас становится 11 мест, на которые могут рассесться 11 учеников, а это 11!, наши 3 ученика, сидящие вместе на одном месте могут между собой сесть 3! способами, следовательно:

Задача №3

Из урны, содержащей 19 белых и 31 черных шаров, вынимаются два шара.

а) Найти вероятность тою, что шары разных цветов.

б) Найти вероятность того, что шары одного цвета.

Решение

Находим вероятность того, что шары будут разных цветов:

Вероятность того, что оба вытащенных шара будут разных цветов это - вероятность того, что первый шар будет белым, а второй черными или того, что первый шар будет черным, а второй – белым. Она равна сумме соответствующих вероятностей.

Вероятность того, что первый вынутый шар белый:

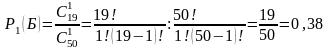
Вероятность того, что второй вынутый шар черный:

Находим вероятность, что первый шар будет белый, второй черный:

Вероятность того, что первый вынутый шар черный:

Вероятность того, что второй вынутый шар белый:

Находим вероятность, что первый шар будет черный, второй белый:

Вероятность, что шары будут разноцветные равна сумме полученных вероятностей.

Находим вероятность, что шары будут одного цвета. Тут возможно 2 варианта – либо оба шара белые, либо оба черные.

1.Оба шара белые.

Вероятность, что первый вынутый шар белый:

Вероятность, что второй вынутый шар белый:

Тогда вероятность, что подряд были выбраны белые шары равна:

2.Оба шара черные:

Вероятность, что первый вынутый шар черный:

Вероятность, что второй вынутый шар черный:

Тогда вероятность, что подряд были выбраны черные шары равна:

Вероятность того, что шары одного цвета находим по формуле сложения вероятностей:

Задача № 4

Имеются две урны. В первой лежат 14 белых и 19 черных шаров; во второй находятся 31 белых и 16 черных шаров. Из первой урны во вторую перекладывают один шар.

Какова вероятность после этого вынуть:

а) белый шар из I урны

б) белый шар из II урны.

Решение

Всего шаров в первой урне 14+19=33, во второй – 31+16=47.

При перекладывании шара из первой урны во вторую возможны следующие варианты: 

а) событие Н₁ вынули белый шар:

 

б) событие Н₂ вынули черный шар:

Далее рассмотрим следующие варианты:

Если из первой урны вынули белый шар, то, в ней будет 14 белых 18 черных шаров, а всего будет 32. Во второй же урне будет 31 белых и 16 черных шаров, а всего их будет 48.

Тогда вероятность того что белый шар будет вынут из первой урны равна:

А вероятность того что белый шар будет вынут из второй урны равна:

Если из первой урны вынули черный шар, то в ней будет 14 белых 18 черных шаров, а всего будет 32. Во второй урне будет 31 белых и 17 черных шаров, а всего их будет 48.

Тогда вероятность того что белый шар будет вынут из первой урны равна:

А вероятность того что белый шар будет вынут из второй урны равна:

Тогда, по формуле полной вероятности находим вероятность того, что выбранный белый шар был из первой урны будет:

Вероятность того, что выбранный белый шар был из второй урны будет: