6.3 Гетерогенный катализ

6.3.1. Общие понятия

В рамках классификации катализа по фазовому признаку мы подробно рассмотрели гомогенный катализ. Теперь мы перейдем к детальному обсуждению гетерогенного катализа, в котором используются твердые катализаторы. В связи с огромной важностью эту область также называют промышленным катализом.

В условиях гетерогенного катализа твердые катализаторы отличаются рядом особенностей от катализаторов гомогенных процессов, главным образом - это высокая механическая и термическая стабильность твердых катализаторов. Обычно твердым катализаторам может быть придана любая форма (сферы, таблетки, полые цилиндры, кольца, блоки и т.п.), они легко размещаются в традиционных промышленных аппаратах; кроме того, твердые катализаторы легко отделяются от реакционной смеси (почти без потерь, типа уноса частиц). Поэтому практически во всех непрерывных промышленных процессах нефтепереработки, нефтехимии и основного химического синтеза используются твердые катализаторы.

Твердые катализаторы имеют определенный физические свойства, основными из которых являются удельная поверхность (м²/г), объем (мл/г) и структура пор, плотность (истинная и насыпная). Высокая удельная поверхность катализаторов (обычно от 10 до сотен м²/г) достигается за счет развитой системы пор, размером 1-10 нм (микропоры) и 100-1000 нм (макропоры).

По типу соединений твердые катализаторы могут быть металлами, применяются также оксиды, гидриды, сульфиды, карбиды, нитриды, а также их смеси. Кроме того, возможно применение солей и твердых кислот (особенно гетерополикислот).

Различают катализаторы массивные и нанесенные на носитель. Использование носителя основано на том, что в твердом катализаторе «работает» главным образом, тонкий слой поверхности, в котором имеются так называемые активные центры. Поэтому часто каталитически активную массу наносят на носитель, что позволяет снизить затраты на обычно более дорогой активный компонент, увеличить его дисперсность, часто также улучшаются и другие физические свойства, например, механическая прочность, теплопроводность и др.).

Обычно катализатор представляет собой смесь каталитически активного материала (например, металла) с добавкой промотора на носителе. Носитель используется для увеличения дисперсности частиц катализатора, доступности активных центров, улучшению пористой структуры. Носитель не обладает собственной каталитической активностью и не взаимодействует с каталитически активным материалом. Поэтому в качестве носителей обычно используют химически инертные, тугоплавкие оксиды с развитой поверхностью, например, активный углерод, диоксид кремния, оксид алюминия, алюмосиликаты, оксиды магния, цинка и др. Удельная поверхность носителей обычно заключается в диапазоне от 10 до 400 м²/г.

Кроме того, твердые катализаторы могут содержать промоторы. Промотор, как и носитель, не обладает каталитической активностью, но взаимодействует с каталитически активным материалом и в малых добавках улучшает некоторые эксплуатационные свойства катализатора. Например, добавка 0,2% рения (и хрома) к платине сильно повышает селективность и стабильность катализатора ароматизации в отношении спекания. Добавка 1-2% щелочи (К₂О) к железным катализаторам синтеза увеличивает выход аммиака, а в синтезе Фишера-Тропша улучшают селективность по высшим углеводородам и спиртам (подавляют метанирование).

6.3.2 Основные типы твердых катализаторов

Рассмотрим теперь основные типы катализаторов, используемые в различных промышленных процессах. Для процессов кислотно-основного катализа, таких как крекинг, гидратация, дегидратация, изомеризация и др. катализатор должен обладать способностью передавать протоны реагентам. Поэтому лучшими катализаторами будут сильные кислоты, такие как цеолиты в Н-форме, алюмосиликаты, кислоты, в том числе суперкислоты и ГПК.

Для процессов гидро-дегидрогенизации, таких как гидрирование ненасыщенных соединений, гидрообессеривание нефтепродуктов, дегидрирование парафинов в олефины, ароматизации катализатор должен обладать способность к активации водорода. Обычно в качестве катализаторов таких процессов используют металлы VIII группы их оксиды и сульфиды.

В другом важном классе окислительных процессов обычно используют катализаторы – оксиды переходных металлов, например, оксиды ванадия, меди, хрома, молибдена, марганца и др.

6.3.3. Области протекания гетерогенно-каталитических процессов

Общими стадиями гетерогенного катализа являются диффузия реагентов к поверхности и в порах катализатора, затем протекают процессы адсорбции-координации, активации реагентов и собственно реакции, и окончательно продукты десорбируются с поверхности в объем реакционной смеси. В зависимости от условий процесса, каждая из перечисленных стадий может лимитировать суммарный процесс.

Поэтому задача описания процесса дополняется анализом области его протекания. Так, если медленной стадией является диффузия в среде или в порах катализатора, говорят, что реакция протекает во внешне- или внутридиффузионной области. Реже наблюдается десорбционная область, когда процесс лимитирует десорбция. Для полной реализации каталитического действия необходимо, чтобы все эти процессы протекали быстрее, чем собственно реакция на поверхности катализатора. Это особенно важно в случае сильно экзотермических процессов, когда при малой интенсивности процессов переноса тепла и вещества возможно тепловое воспламенение в слое катализатора, приводящее к аварии реактора.

1

lg r

Рис. 6.6 Области протекания гетерогенного каталитического процесса: 1-кинетическая, 3, 2- внешне- и внутридиффузионная, 4-гомогенная некаталитическая

E₄ > E₁ > E₂ >> E₃ ~5-10 kJ/mole

E₁ ~ 2 E₂

1/Т

Рис. 6.7. Профили концентрации в областях протекания гетерогенного каталитического процесса

обл.	Градиент С	Эффективность катализатора
1	Мал, до 3% С = Сs ~ СL	Около 100%
2	В объеме мал; в поре большой	10-90%, часть пор не работает
3	В объеме большой; в поре очень больш. Сs ~0	около 1%; реакция идет на внешней поверхности катализатора
4	очень большой в объеме и порах Сs= 0	реакция идет в газовой фазе

Вместо С_п дать С_s

И вместо С_г дать С_g

6.3.4 Диффузионные стадии катализа

Сначала рассмотрим диффузионные области протекания катализа. В случае быстрой реакции на поверхности катализатора суммарная скорость процесса может быть ограничена скоростью диффузионного подвода из ядра потока к внешней поверхности катализатора. Скорость диффузии вещества в стационарном состоянии определяется уравнением Фика:

J = β∆C, (6.14)

где β=D/δ ; δ – толщина приведенной пленки и ∆C градиент (разность) концентраций между ядром потока и вблизи поверхности. Коэффициент массопередачи β является функцией от размера частиц, коэффициента диффузии, скорости потока и вязкости среды,

Рассмотрим случай, когда реакция на поверхности имеет 1й порядок по реагенту А (это справедливо, когда поверхностная концентрация вещества мала, т.е. заполнение поверхности b_AP_A << 1. В стационарном состоянии скорости диффузии и реакции равны, т.е. J = r или:

β(C_о- С_п) = k bC_п (6.15)

Из (16) можно найти C_п = βC_о/(kb + β) (6.16)

Подставляя это значение С_п в кинетическое уравнение, получим:

r = kbβC_о/(kb + β) = k_эфC_о (6.17)

где k_эф = kbβ/(kb + β) (6.18)

Уравнение 19 часто интерпретируют, как метод сложения сопротивлений (по аналогии с электрическим током), т.е. суммарное сопротивление слагается из диффузионного и реакционного (на поверхности)

1/k_эф =1/β + 1/kb (6.19)

Из (18) очевидны 2 предельных случая:

1й : kb >> β и r = βC_о , (6.20)

Такая область называется внешнедиффузионной, и

2й: kb << β, тогда

r = kbC_о (6.21)

Эта область называется внешнекинетической.

Далее более подробно рассмотрим процесс диффузии в порах и реакцию n-го порядка, протекающую внутри поры. Поверхность считается плоской, и диффузия идет только по нормали (x) от поверхности внутрь пористой массы.

В стационарном состоянии скорость накопления вещества (определяется по 2-му закону Фика) равна скорости реакции:

D_э(d²C/dx²) - k_эCⁿ= 0 (6.22)

Из решения д.у. (23) находится величина dC/dx и тогда можно рассчитать диффузионный поток, который равен наблюдаемой скорости реакции:

J_D = 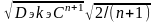(6.23)

Из этого уравнения видно, что наблюдаемая скорость реакции пропорциональна среднему геометрическому из скорости реакции и скорости диффузии.

В этой задаче естественным масштабом длины является величина (D_э /k_эC^n-1)^0,5, которую называют эффективной глубиной проникновения реакции в слой пористого материала L. Для реакции 1-го порядка L= (D_э /k_э)^0,5. Очевидно, что чем больше скорость реакции, тем меньше глубина проникновения реакции в пористый материал.

6.3.5 Адсорбционные стадии катализа

Принципиальное отличие реакций на поверхности от гомогенных процессов заключается в том, что реагируют адсорбированные молекулы или их фрагменты, а не свободные или ассоциированные (с растворителем) частицы. Сорбция является следующей необходимой стадией реакции в гетерогенной системе. В зависимости от фазового пространства, в котором протекает процесс, различают абсорбцию (во всем объеме) и адсорбцию (на поверхности). Эти процессы протекают на поверхности раздела фаз, которая представляет собой реакционное пространство для гетерогенных процессов.

Для катализа адсорбция фактически представляет собой первую стадию каталитического действия. Принципиальное отличие гетерогенно-каталитических реакций заключается в том, что взаимодействуют не свободные молекулы, как в гомогенных процессах, а адсорбированные частицы. Поэтому для реакции A + B  D на поверхности катализатора закон действующих масс имеет вид:

r = k _A_B (6.24)

где _A и _B – концентрации реагентов на поверхности. Таким образом, для описания кинетики каталитических реакций необходимо найти связь между неизвестной концентрацией реагентов на поверхности θ_i и их концентрацией в объеме вокруг катализатора. Для этого нам предстоит более подробно рассмотреть процесс адсорбции.

Адсорбция представляет собой процесс поглощения вещества - адсорбата на поверхности поглотителя. Вещество - поглотитель называется адсорбентом/катализатором. Адсорбция обусловлена притяжением между частицами на поверхности адсорбента, обладающими избыточной энергией, и молекулами жидкого или газообразного адсорбата, и поэтому является самопроизвольным экзотермическим процессом. По энергетике взаимодействия в системе адсорбат/адсорбент можно выделить физическую адсорбцию и хемосорбцию.

При физической адсорбции молекулы адсорбата связаны с поверхностью слабыми силами ван-дер-Ваальса, этот быстрый процесс не является специфичным и по своей природе близок к конденсации. Теплота такого процесса обычно составляет 1-5 кДж/моль. В случае хемосорбции равновесие устанавливается существенно медленнее, а тепловой эффект гораздо больше, чем при физадсорбции, и составляет от 40 до 1000 кДж/моль. Видно, что по тепловому эффекту хемосорбция близка к химической реакции.

Другим отличием хемосорбции является ее специфичность, т.е. зависимость величины поглощения от природы пары адсорбент/адсорбат. Например, водород плохо хемосорбируется на оксидах и хорошо на металлах VIII группы. Вода и диоксид углерода хорошо хемосорбируются на оксидах металлов и плохо на металлах и т.п.

Зависимость равновесного количества адсорбата при хемосорбции от давления газа (или концентрации вещества в растворе) при постоянной температуре называется изотермой адсорбции. Наиболее простой и популярной изотермой адсорбции является изотерма Лангмюра, которая выведена для модели идеального адсорбированного слоя.

Эта модель включает в себя 3 допущения:

1) частица адсорбата (A) взаимодействует с одним центром Z на поверхности,

2) все центры на поверхности адсорбента энергетически равноценны и

3) между частицами, адсорбированными на поверхности, отсутствует сильное взаимодействие.

В рамках такой модели хемосорбцию можно представить как обратимую реакцию:

A + Z  AZ (SR 1)

В состоянии равновесия скорости процессов адсорбции и десорбции равны между собой

k_aР_А[Z] = k_д[AZ], (6.25)

где [Z] и [AZ] концентрации свободных и заполненных центров на поверхности. Из (6.26) с учетом очевидного уравнения баланса:

[Z] + [AZ] = [Z]_o , при t=0 [Z]= [Z]_o (6.26)

найдем выражение изотермы адсорбции Лангмюра для безразмерной концентрации на поверхности

θ_A= [AZ]/[Z]_o = b_AP_A/(1+ b_AP_A) (6.27)

Здесь b_A = k_a/k_д - константа равновесия адсорбции или адсорбционный коэффициент газа А,

b = b_oexp(Q_a/RT), (6.28)

где Q_a – это теплота адсорбции А на поверхности.

В случае адсорбции нескольких газов, выражение изотермы адсорбции Лангмюра имеет вид

θ_i= b_iP_i/(1+∑ b_iP_i) (6.29)

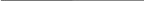
θi 2 1	Рис. 6.8. Зависимость заполнения поверхности от давления (концентрации) вещества в объеме. 1- область Генри; 2- область насыщения поверхности
Давление (Рi или Сi)

При адсорбции некоторых молекул (например, О₂ , Н₂, галогены и др.) на поверхности происходит диссоциация, поэтому выведем уравнение изотермы для случая т.н. диссоциативной адсорбции:

A₂ + 2Z  2AZ (SR 2)

В состоянии равновесия скорости процессов адсорбции и десорбции равны между собой

k_aР_А[Z]² = k_д[AZ]² (6.30)

и с учетом уравнения баланса:

[Z] + [AZ] = [Z]_o , при t=0 [Z]= [Z]_o (6.31)

найдем выражение для изотермы диссоциативной адсорбции

θ_A= 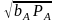/(1+ ) (6.32)

Однако обычно центры на поверхности адсорбента энергетически неравноценны, и поэтому теплота адсорбции веществ зависит от заполнения поверхности θ. Действительно при измерении дифференциальной теплоты адсорбции, обнаружено, что Q_a(θ) является убывающей функцией. В случае такой неоднородной поверхности уравнение Лангмюра может быть справедливо только для малого участка поверхности с близкими значениями теплоты адсорбции. Для нахождения уравнения изотермы адсорбции необходимо проводить интегрирование по всем участкам поверхности с учетом функции распределения центров по теплотам адсорбции f(Q).

Для такой неоднородной поверхности общее выражение изотермы адсорбции имеет вид:

θ_i= ∫f(Q)dQ*b_оexp(Q/RT)P/(1+ b_оexp(Q/RT)P) (6.33)

Опуская сложные выкладки, отметим, что в случае, когда f(Q) является экспоненциальной функцией, т.е. теплота адсорбции экспоненциально убывает с увеличением θ, после интегрирования, в области средних заполнений, получается уравнение изотермы Фрейндлиха

θ = bP^1/n (6.34),

где b и n связаны с параметрами экспоненциального распределения теплоты адсорбции.

В случае, если теплота адсорбции линейно убывает с увеличением θ, после интегрирования, в области средних заполнений, получается уравнение изотермы Фрумкина

θ = ART*ln(fP) (6.35)

где A и f связаны с параметрами линейного распределения теплоты адсорбции

Из уравнений (30, 35 и 36) видно, что поверхностная концентрация вещества является сложной (гиперболической, степенной или логарифмиской) функцией его парциального давления в объеме (рис. 6.4), что существенно усложняет вид кинетических уравнений для реакций в гетерогенной системе.

Таким образом, современная кинетика располагает необходимыми моделями и уравнениями связи между концентрациями вещества на поверхности и в объеме газовой фазы. Это указанные выше изотермы Ленгмюра (для энергетически однородной поверхности) и изотермы Фрейндлиха и Фрумкина (для реакций на энергетически неоднородной поверхности).

6.3.6 Основные кинетические уравнения для реакции на поверхности

Продемонстрируем теперь вывод кинетического уравнения реакции 1го порядка на поверхности A à D, протекающей в реакторе идеального вытеснения. По такой схеме проходят реакции элиминирования, в том числе крекинг, дегидрирование, дегидратация и др. Уравнение скорости для таких реакций имеет вид:

r = k q_A (6.36)

Используя уравнение Лангмюра (6.30) для выражения связи θ = f(P), найдем:

θ_А= b_АP_А/(1+ b_АP_А+ b_DP_D) (6.37)

и окончательно

r = kb_АP_А/(1+ b_АP_А+ b_DP_D) (6.38)

Из анализа следуют три предельных случая:1) при малых заполнениях поверхности b_AP_A и b_DP_D<< 1 концентрация реагента на поверхности пропорциональна его парциальному давлению в газовой фазе. В этой области выполняется закон Генри и наблюдаемый порядок реакции по реагенту А равен 1, а порядок по продукту - близок к 0.

2) при больших заполнениях поверхности реагентом, b_AP_A>> b_DP_D> 1 наблюдаемый порядок реакции по реагенту и продукту будет близок к нулю.

3) при больших заполнениях поверхности b_DP_D >> b_AP_A> 1 наблюдаемый порядок реакции по реагенту А равен 1 и по продукту D близок к -1.

Следовательно, в отличие от гомогенных реакций, в гетерогенных реакциях 1го порядка, протекающих на поверхности катализатора, с ростом давления и адсорбционной способности наблюдаемый порядок по реагенту А уменьшается от 1 до нуля (или от 0,5 до нуля в случае диссоциации молекул). В то же время порядок по продукту может изменяться от 0 (слабая адсорбция продукта) до -1 (сильная адсорбция продукта).

Покажем теперь, как с использованием (6.39), можно найти зависимость степени превращения от времени реакции A à D, т.е. х_А(τ) в реакторе идеального вытеснения. Для этого напомним основное интегральное уравнение кинетики:

t = C_А(0)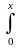 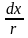(6.39)

где t = V_c/Q время контакта реакционной смеси с катализатором.

Уравнение (6.39) содержит три переменных: P_А, P_D и τ, поэтому для решения (6.40) надо выразить скорость реакции как функцию степени превращения.

Для представления (6.39) в виде х(τ), надо выразить текущие P_А, P_D как функции степени превращения:

P_А= P₀ (1-х) и P_D = P₀х (6.40)

тогда

r(х) = kb_АР₀(1-х) / (1+ b_АP₀ (1-х) + b_DP₀х) (6.41)

и уравнение (6.40) можно представить как

kb_АР₀ t = C_А(0) dx [1+ b_АР₀(1-х)+ b_DР₀х] / (1-х) (6.42)

Этот интеграл берется по частям, и общее решение имеет вид суммы:

kb_АRT t = Р₀(b_А-b_D)х - (1+ b_DР₀) ln (1-x) (6.43)

или - [ln (1-x)]/х = -Р₀(b_А-b_D)/(1+ b_DР₀) + kb_АRT/(1+ b_DР₀)* t/x (6.43а)

Применимость уравнений типа (6.42) (Фроста) для описания экспериментальных данных проверяется в линеаризующих координатах

“-ln (1-x)]/х от t/x”. Дать график этой зависимости…

Тогда константу скорости можно определить из наклона прямой, отрезка на оси ординат, и отношения адсорбционных коэфф. b_D /b_А:

k = (tg α/отр.)* C₀/(1-b_D /b_А) (6.44)

В результате проведенного анализа и определения констант уравнения (6.42) можно рассчитать время контакта реагентов с катализатором для достижения заданной степени превращения, или наоборот, рассчитать степень превращения сырья при заданном времени контакта.

Из уравнения r = kb_АP_А/(1+ b_АP_А+ b_DP_D) (6.38)

можно также найти связь наблюдаемой энергии активации, определяемой из температурной зависимости начальной скорости реакции, и истинной энергией активации. При малых заполнениях поверхности справедливо выражение r₀ = kb_АP₀ или r₀ = k₀ exp(-E/RT)*b_0Аexp(Q_a/RT)*P₀

r = k₀*b_0АP₀ exp[(-E+Q_a)/RT)] или (6.45)

ln r = ln (k₀*b_0АP₀) + [(-E+Q_a)/RT)] (6.46)

откуда видно, что наблюдаемая энергия активации меньше истинной на величину теплоты адсорбции реагента: E_н = Е - Q_a

Аналогичен вывод кинетического уравнения реакции 2го порядка на поверхности 2A à D, используя уравнение изотермы Лангмюра (6.30).

Уравнение скорости реакции имеет вид:

r = k q_A² (6.47)

Используя (6.30), найдем окончательно

r = kb_А²P_А²/(1+ b_АP_А+ b_DP_D)² (6.48)

Из анализа (6.39) также следуют два предельных случая:

1) при b_AP_A и b_DP_D<< 1 концентрация реагента на поверхности пропорциональна квадрату его парциального давления в газовой фазе. В этой области наблюдаемый порядок реакции по реагенту А равен 2, а порядок по продукту - близок к 0.

2) при больших заполнениях поверхности b_AP_A>> b_DP_D> 1 наблюдаемый порядок реакции по реагенту и продукту будет близок к нулю.

3) при больших заполнениях поверхности b_DP_D >> b_AP_A> 1 наблюдаемый порядок реакции по реагенту А равен 2 и по продукту D близок к -2.

Таким образом, очевидно, что, в отличие от гомогенных реакций, в гетерогенных реакциях 2го порядка, протекающих на поверхности катализатора, с ростом давления и адсорбционной способности наблюдаемый порядок по реагенту А уменьшается от 2 до нуля. В то же время порядок по продукту может изменяться от 0 (слабая адсорбция продукта) до -2 (сильная адсорбция продукта).