
- •Введение
- •§1. Электрические цепи постоянного тока
- •1.1. Источник э.Д.С. И источник тока
- •1.2. Допустимые и недопустимые комбинации соединений идеальных источников в электрических цепях
- •1.3. Методы расчета электрических цепей
- •1.3.1. Метод эквивалентного генератора
- •1.3.2. Принцип наложения и метод наложения
- •1.3.3. Метод, основанный на использовании первого и второго законов Кирхгофа
- •1.3.4. Метод контурных токов
- •1.3.5. Метод узловых потенциалов
- •1.3.6. Сравнение метода контурных токов и метода узловых потенциалов
- •1.3.7. Преобразование звезды в треугольник и треугольника в звезду
- •§2. Электрические цепи синусоидального переменного тока
- •2.1. Синусоидальный ток и его основные характеристики
- •2.2. Символический метод расчета цепей синусоидального тока
- •2.3. Мощность в цепи синусоидального переменного тока
- •§4. Переходные процессы в электрических цепях
- •4.1. Общий подход к анализу переходных процессов
- •4.2. Классический метод анализа переходного процесса
- •4.3 Формализация классического метода
- •4.4. Переходные процессы в цепях синусоидального переменного тока
- •4.5. Операторный метод анализа переходных процессов
1.3.7. Преобразование звезды в треугольник и треугольника в звезду
В электрических цепях имеют большое распространение структуры из трех ветвей в виде трехлучевой звезды и треугольника. Рассмотрим, в частности, эти фигуры, состоящие из резисторов: звезду сопротивлений и треугольник сопротивлений (рис. 1.3.14).
При расчете электрических цепей часто оказывается целесообразным участок цепи, имеющий структуру звезды сопротивлений, преобразовать в треугольник сопротивлений, или наоборот, что позволяет иногда существенно упростить расчет цепи. Внешние, окружающие фигуру элементы цепи «не замечают» подобных преобразований, ибо потенциалы звезды и треугольника в процессе преобразования остаются неизменными.
Задача 1.3.16 (рис. 1.3.14). Осуществить переход от звезды к треугольнику, что означает необходимость выразить резисторы R12, R23, R13 треугольника через величины резисторов R1, R2, R3 звезды. Такой переход можно осуществить, используя метод узловых потенциалов.

Рис. 1.3.14
Решение. Для звезды (ее единственного
узла при потенциале
![]() )
запишем уравнение
)
запишем уравнение
I1 + I2 + I3 = 0. (1.3.14.1)
Выразим токи I1, I2, I3 через потенциалы и проводимости резисторов:
I1 = (1 ‑ 0) g1; I2 = (2 ‑ 0) g2; I3 = (3 ‑ 0) g3.
Схема треугольника отличается от схемы звезды отсутствием потенциала 0, поэтому в процессе преобразования необходимо избавиться от потенциала 0, выразив его через другие потенциалы. Подставим значения I1, I2, I3 в исходное уравнение (1.3.14.1) и решим его относительно0:
![]()
![]() .
.
Теперь в выражениях для токов I1, I2, I3 можно избавиться от потенциала 0. Например, для тока I1
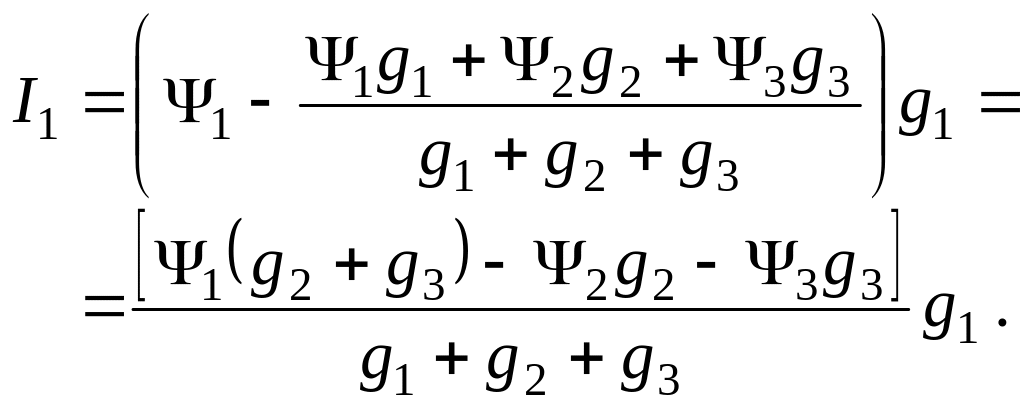 (1.3.14.2.)
(1.3.14.2.)
Выразим теперь ток I1 через токи треугольника
![]() (1.3.14.3)
(1.3.14.3)
Сравним уравнения (1.3.14.2) и (1.3.14.3). Они состоят из трех членов с потенциалами 1, 2, 3. Полагая, что эти потенциалы одинаковы в обеих схемах, приходим к выводу, что коэффициенты при них так же должны быть равны:
![]() . (1.3.14.4)
. (1.3.14.4)
Аналогично можно найти g23:
![]() .
.
Полученные выражения легко запоминаются, если заметить их следующие свойства:
а) в знаменателе всех выражений стоит сумма проводимостей звезды,
б) в числителе стоят проводимости звезды, прилегающие к соответствующей проводимости треугольника (см. рис. 1.3.14).
Задача 1.3.17. Осуществить переход от треугольника к звезде, что означает необходимость выразить резисторы звезды через величины резисторов треугольника. Такое преобразование треугольника в звезду можно осуществить следующим образом: выразим, например, выражения (1.3.14.4) через сопротивления:
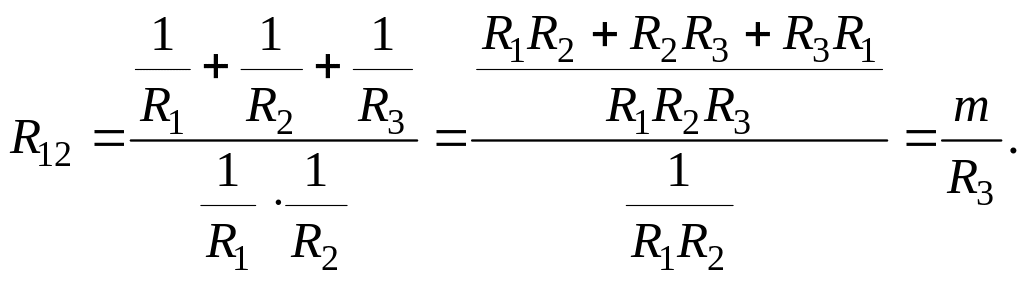 (1.3.14.5)
(1.3.14.5)
Аналогично
![]() ;
;
![]() ,
где
,
где
![]() ,
откуда
,
откуда
![]() ;
;
![]() ;
;
![]() . (1.3.14.6)
. (1.3.14.6)
Подставив (1.3.14.6) в (1.3.14.5), получим
![]() ,откуда
,откуда
![]() .
.
Рис. 1.3.15a
![]() ,
,
![]() ,
,
![]() .
.
Задача 1.3.18 (для самостоятельного решения). На рис. 1.3.15a Rн =R, R1 = R2 = R3 =R, R12 = R23 = R13 = 3R. Найти ток в нагрузке Rн. Решение рекомендуется осуществить путем преобразования звезды резисторов R1, R2, R3 в треугольник резисторов.
§2. Электрические цепи синусоидального переменного тока
2.1. Синусоидальный ток и его основные характеристики
Рис. 2.1.1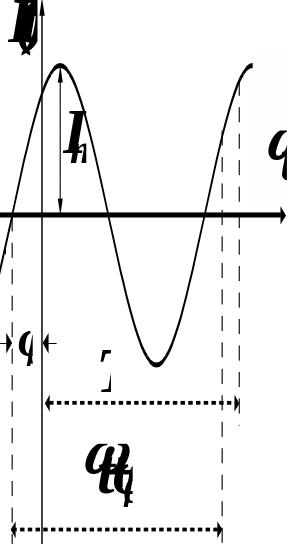
![]() ,
называется синусоидальным переменным
током. Эта форма тока является простейшей
из переменных периодических токов
с точки зрения метода гармонического
анализа, который утверждает, что
любой ток произвольной формы может
быть представлен суммой токов
синусоидальной формы.
,
называется синусоидальным переменным
током. Эта форма тока является простейшей
из переменных периодических токов
с точки зрения метода гармонического
анализа, который утверждает, что
любой ток произвольной формы может
быть представлен суммой токов
синусоидальной формы.
Ток может быть изображен графически на временной шкале (рис. 2.1.1).
Синусоидально изменяющаяся функция
определяется тремя величинами:
амплитудой, угловой частотой и начальной
фазой. Амплитуда Im
есть максимальное значение функции.
Аргумент функции
![]() называют фазой. Фаза характеризует
состояние колебания в данный момент
времени t.
называют фазой. Фаза характеризует
состояние колебания в данный момент
времени t.
Коэффициент , называемый круговой (угловой) частотой, характеризует скорость нарастания фазы, 0 – начальная фаза при t = 0.
Иногда фазу представляют через частоту f или период T:
![]() .
(2.1.1)
.
(2.1.1)
Переменные синусоидальные токи и
напряжения удобно изображать также на
т. н. комплексной плоскости в виде
вектора
![]() ,
вращающегося со скоростью
(рис. 2.1.2):
,
вращающегося со скоростью
(рис. 2.1.2):
![]() , (2.1.2)
, (2.1.2)
Рис. 2.1.2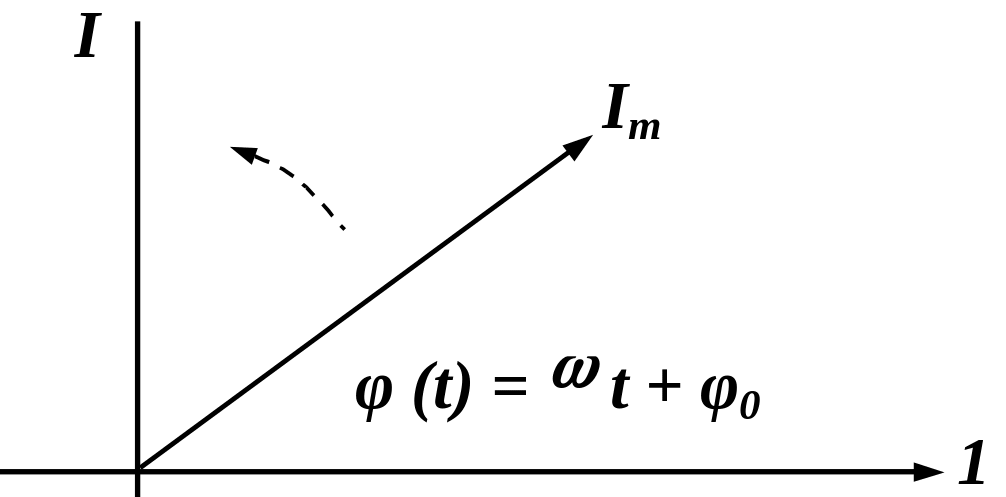
Известно, что в электрической цепи любой электрический процесс может быть описан системой дифференциальных уравнений. Например, для цепи, состоящей из последовательного соединения E, R, L, C можно написать уравнение Кирхгофа в дифференциальной форме:
![]() . (2.1.3)
. (2.1.3)
Очевидно, что это уравнение справедливо и для частного случая – синусоидального переменного тока. Подставим в него выражение (2.1.2.) для тока:
![]()
![]()
![]() . (2.1.4)
. (2.1.4)
Рис. 2.1.3
Рис. 2.1.4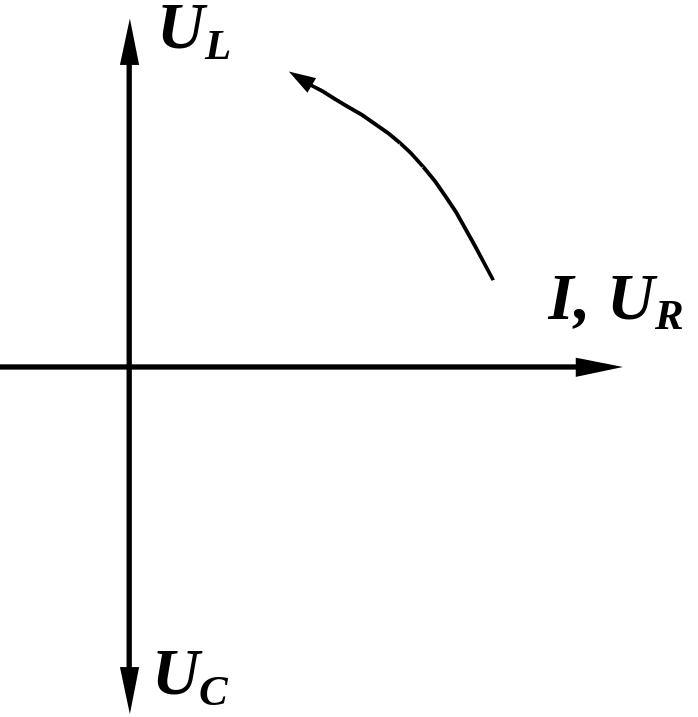
Из рис. 2.1.4 видно следующее:
Напряжение UL на индуктивности опережает ток на 90 .
Напряжение UC на емкости отстает от тока на 90 .
Между напряжениями UL и UC имеет место фазовый сдвиг 180 .
Напряжение UR на сопротивлении совпадает по фазе с током.
Следует оговориться, что L и C предполагаются идеальными, т. е. в них отсутствуют потери электрической энергии.
