1.3.4. Метод контурных токов

Метод контурных токов может рассматриваться как дальнейшее развитие метода, использующего законы Кирхгофа. В качестве неизвестных величин в методе используются т. н. контурные токи, т. е. полагают, что в каждом неза­висимом контуре цепи течет свой контурный ток. Это дает возможность огра­ни­читься составлением уравнений только по второму закону Кирхгофа и, т. о., иногда существенно уменьшить число урав­нений системы. Реальные токи ветвей на­хо­дятся суммированием контурных токов. Как будет показано ниже, этот метод имеет еще и то преимущество, что в наибольшей степени возможна матема­тическая формали­за­ция ре­ше­ния системы уравнений.

Рис. 1.3.8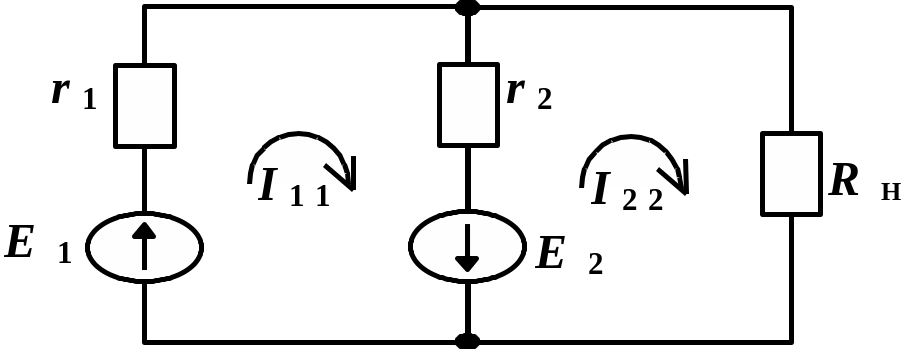

Задача 1.3.9. На рис. 1.3.8 E₁ = 10 В, E₂ = 30 В, r₁ = 2 Ом, r₂= 3 Ом, R_н = 4,8 Ом. Найти ток и напряжение на нагрузке R_н, пользуясь методом контурных токов.

Решение. По второму закону Кирхгофа необходимое число уравнений определяется условием M – (N – 1), где M – число ветвей, N – число узлов, или число независимых контуров цепи:

1. E₁ + E₂ = I₁₁ r₁ + (I₁₁ – I₂₂) r₂;

2. – E₂ = (I₂₂ – I₁₁) r₂ +I₂₂ R_н.

Решение системы уравнений приводит к нахождению контурных токов I₁₁, I₂₂, а через них и токов ветвей:

I₁ = I₁₁, I₂ = I₁₁ – I₂₂, I_н = I₂₂. 

Приведем систему к следующему виду:

1. (r₁ + r₂) – r₂ I₂₂ = E₁ + E₂;

2. – r₂ I₁₁ + (R_н + r₂) I₂₂ = – E₂.

Представим систему уравнений в матричной форме:

_. (1.3.4.1)

Система уравнений обладает определенными свойствами, учитывая которые можно существенно облегчить ее решение.

1. В диагональ матрицы сопротивлений, называемую главной, входят т. н. полные сопротивления контуров:

(r₁ + r₂) = R₁₁ – сопротивление первого контура;

(r₂ + R_н) = R₂₂ – сопротивление второго контура.

2. Остальные члены матрицы со знаком минус есть т. н. взаимные сопротивления, т. е. смежные сопротивления между контурами:

– r₂ = R₁₂ – сопротивление между первым и вторым контурами,

– r₂ = R₂₁ – сопротивление между вторым и первым контурами.

3. Система симметрична относительно главной диагонали:

R₁₂ = R₂₁.

В правой части уравнений имеем сумму электродвижущих сил каждого контура.

E₁ + E₂ = E₁₁ – сумма э.д.с. первого контура,

– E₂ = E₂₂ – сумма э.д.с. второго контура.

Э.д.с. берется со знаком «плюс», если его направление совпадает с направлением обхода контура, и «минус», если его направление встречное.

Замечание. Все качества системы уравнений, перечисленные в пунктах 1 – 4, имеют место при условии, что направление обхода контуров одинаково.

В общем виде система уравнений произвольного порядка теперь может быть представлена в виде

[R]  [I] = [E] или

_.

Решение системы может быть осуществлено, например, с помощью правила Крамера:

.

Здесь | R | есть определитель системы, | _NN | – определитель, полученный путем замены в определителе | R | N-го столбца столбцом матрицы электродвижущих сил.

Продолжим решение задачи, подставив численные значения в уравнения (1.3.4.1):

;

;

;

; ; .

Задача 1.3.10 (рис. 1.3.9). Составить систему уравнений по методу контурных токов.

Решение. Поскольку для контуров с источниками тока уравнения не составляются, система будет иметь два уравнения:

1. ( I₁₁ – J₁) R₁ + (I₁₁ + J₃) R₂ + (I₁₁ – I₂₂) R₄ = E₂; 

2. I₂₂ R₅ + ( I₂₂ – I₁₁) R₄ =  – E₄.

Приведем к каноническому виду

1. I₁₁ (R₁ + R₂ + R₄) – I₂₂ R₄ = E₂ + J₁ R₁ – J₃ R₂; 

2. – I₁₁ R₄+ I₂₂ (R₄ + R₅) = – E₄. 

Приведем к матричному виду

.

Источники тока (помно­жен­ные на шунтирующие их сопро­тив­ления) оказались в правой части системы уравнений вместе с электро­движу­щими силами, т. о. как бы автомати­чески произошла замена источников тока на источники э.д.с. Следова­тельно, в методе контурных токов нет необходимости предва­ри­тельно осуществлять преобра­зо­ва­ние источников тока в источники э.д.с.

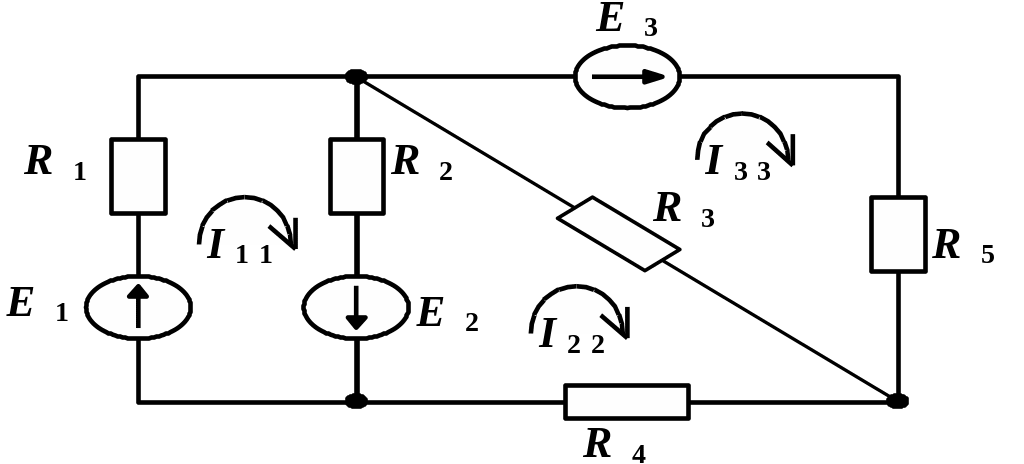
Рис. 1.3.9 Рис. 1.3.10

При известном навыке, используя вышеприведенные правила 1 – 4, систему уравнений цепи можно сразу представить в матричной форме, минуя промежуточные выкладки.

Задача 1.3.11 (для самостоятельного решения). Составить систему уравнений в матричной форме для цепи, представленной на рис. 1.3.10.