4.4. Переходные процессы в цепях синусоидального переменного тока

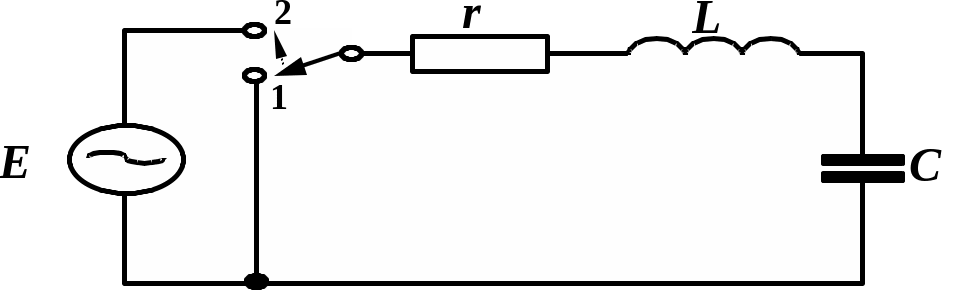
Задача 4.4.1. Рассмотрим вариант переходного процесса в RC – цепи при подключении ее к источнику переменной э.д.с. На рис. 4.4.1 E = 50sin(t–30) B, R = 20 Ом, X_C = 35 Ом, C = 9010^6 Ф, f = 50 Гц. Найти I(t), U_R(t), U_C(t).

Рис. 4.4.1

Решение.

1. Характеристическое уравнение

, откуда

.

2. До подключения к источнику все напряжения и токи в цепи равны нулю. После коммутации, в момент t₀₊

;

	t0–	t0+:	t  
E	–25 B	–25 B	50e30 B
I	0	–1,25 A	1,24e j30 A
UC	0	0	43,4e–60 B
UR	0	–25 B	24,8e j30 A

.

Занесем эти данные в таблицу начальных состояний.

3. По окончании переходного процесса (при t  ) в цепи уста­новятся синусоидальный переменный ток и синусоидальные переменные напряжения, которые удобно представить в рамках символического метода:

 B;

;  B;

 B.

4. Общие решения для тока и напряжений:

I(t) = I_св + 1,24e^j30 ;

.

Решим эти уравнения для момента времени t = 0₊:

–1,25 = I_св + 1,24 sin30 = I_св + 1,240,5 = I_св + 0,62, откуда

I_св = – 0,62 – 1,25 = – 1,87 A;

0 = U_C св + 43,4 sin(–60) = U_C св – 43,40,866 = U_C св – 37,6, откуда

U_C св = 37,6 B ;

–25 = U_R.св + 24,8 sin30= U_R.св + 24,80,5 = U_R.св + 12,4, откуда

U_R.св = –25 – 12,4 = –37,4 B

Подставим результаты в уравнения для тока и напряжений:

I (t) = –1,87 e^555,5t + 1,24 sin( t + 30);

U_C (t) = 37,6 e^555,5t + 43,4 sin( t – 60);

U_R (t) = – 37,4 e^555,5t + 24,8 sin( t + 30).

Рис. 4.4.2а Рис. 4.4.2б

5. На рис. 4.4.2а и 4.4.2б изображены графики переходных процессов U_R и U_C соответственно.

Задача 4.4.2. В какой момент (при какой фазе источника) необходимо разомкнуть ключ K в схеме цепи на рис. 4.4.1, чтобы при размыкании ключа отсутствовал переходный процесс? Предполагается, что в цепи имеет место установившийся процесс, т. е. свободные составляющие тока и напряжений отсутствуют.

Решение. Очевидно, что переходного процесса можно избежать, если ключ разомкнуть в момент, когда напряжение на конденсаторе равно нулю. В этот момент реактивная энергия в цепи отсутствует:

U_C0 sin (t – 60) = 0;  sin (t – 60) = 0;  t – 60= 0; откуда

 t = 60.

Составим уравнение Кирхгофа для контура:

E sin (t – 30) = U_R0 sin (t + 30) + U_C0 sin (t – 60) ;

подставим в него t = 60:

E sin (60 – 30) = U_R0 sin (60 + 30) + U_C0 sin (60 – 60) ;

E sin 30 = U_R0 sin 90 + U_C0 sin 0.

Таким образом, если отключить источник при фазе 30, в цепи будет отсутствовать переходный процесс.

Надо заметить, что (аналогично) если при этой фазе источника подключить к нему цепь, переходный процесс также будет отсутствовать, т. е., в токе и напряжениях цепи будут отсутствовать свободные составляющие.

Рис. 4.4.3

Задача 4.4.3 (для самостоятельного реше­ния). На рис. 4.4.3 L = 16010^6 Гн, E = 20 sin ( t – 30), C = 16010^12 Ф, r = 10 Ом, частота генератора, совпа­дает с резонансной частотой колебательного кон­ту­ра. Найти ток контура и напряжения на индуктивности и емкости.