4.3 Формализация классического метода

Можно обратить внимание на тот факт, что характеристическое уравнение (4.2.1) цепи, представленной на рис. 4.1.1, имеет аналогию с выражением полного сопротивления цепи для синусоидального переменного тока в символическом методе:

.

Если это выражение приравнять к нулю и оператор j заменить опера­тором p, получим характеристическое уравнение (4.2.1).

Эту аналогию можно углубить, понимая под оператором p т. н. обобщенную частоту, т. е. частоту, которая изменяется от бесконечности до нуля при развитии во времени переходного процесса, т. е.

.

В первый момент времени переходного процесса t = 0, p  , т. е. частота переходного процесса бесконечно велика. Для этого момента времени сопротивление индуктивности pL бесконечно велико, сопротивление емкости 1/pC бесконечно мало. Индуктивность равноценна разрыву цепи, емкость – короткому замыканию.

При нарастании времени переходного процесса частота p переходного процесса падает. В результате сопротивление индуктивности pL падает, сопротивление емкости 1/pC растет. В пределе, при t  , сопротивление индуктивности становится равным нулю, сопротивление емкости – бесконечно большой величине. Такая частотная интерпретация, аналогично законам коммутации, может быть использована для анализа начальных условий задачи о переходном процессе и составления таблицы.

Таким образом, цепь на рис. 4.1.1 при переходном процессе обладает сопротивлением:

.

В общем случае для сложных цепей может быть составлена система характеристических уравнений, например, по методу контурных токов (или узловых потенциалов). Определитель этой системы, приравненный к нулю, будет характеристическим уравнением системы

, . (4.3.2)

Таким образом, формально ха­рак­теристическое уравнение есть полное сопротивление цепи на частоте p, приравненное нулю. Пользуясь этим выводом и анало­гией с символическим методом, можно не составлять систему дифференциальных уравнений, а сразу начинать решение задачи с составления системы характе­рис­тических урав­нений. Продемонстрируем выше­сказанное решением задачи с использованием метода контур­ных токов.

Рис. 4.3.1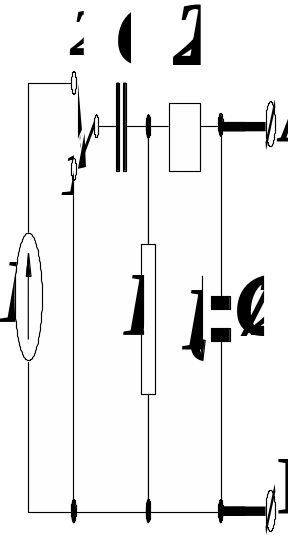

Задача 4.3.1. В цепи, представ­ленной на рис. 4.3.1, найти ток I_C и напряжение U_AB при переклю­чении ключа из положения 1 в положение 2.

Решение. Составим опреде­ли­тель сопротивлений по методу контурных токов и приравняем его к нулю (см. свойства 1–3 в § 1.3.4):

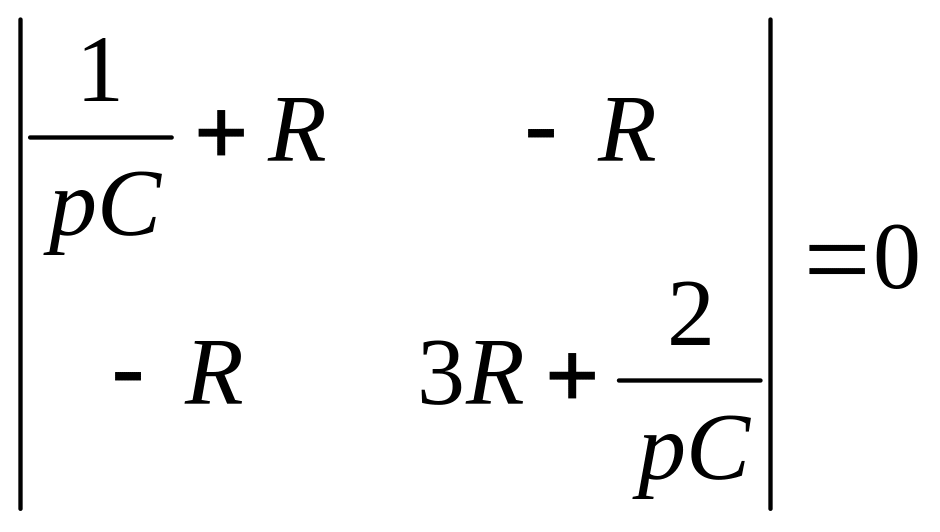; откуда ,

решим полученное уравнение

;

; .

Таким образом, решение для тока будет иметь вид

. (4.3.3)

Решение для напряжения найдем интегрированием решения (4.3.3):

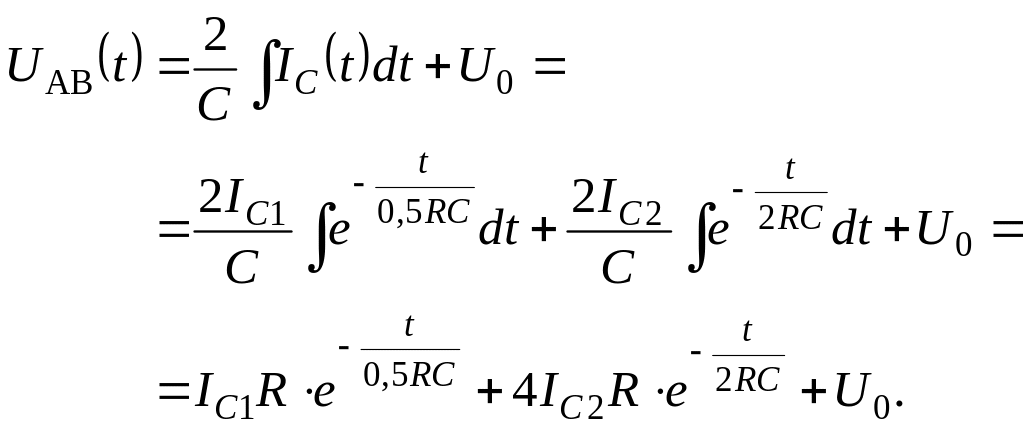(4.3.4)

Составим таблицу начальных условий, пользуясь частотной интерпрета­цией переход­ного процесса. Из таблицы видно, что при­нуж­денные составляющие тока и напряжения I_C 0 и U₀ равны нулю. Найдем решения уравнений (4.3.3) и (4.3.4) для момента :

; , откуда ; .

Окончательное решение для тока

.

Решение для напряжения имеет вид

.

Рис. 4.3.2 Рис. 4.3.3

На рис. 4.3.2 представлен переходный процесс для тока , на рис. 4.3.3 – для напряжения U_AB.

Рис. 4.3.4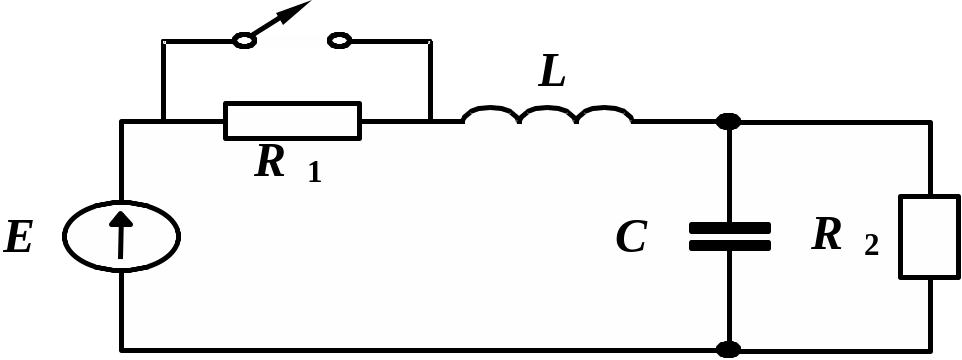

Задача 4.3.2. На схеме рис. 4.3.4 R₁ = R₂ = 10⁵ Ом, L = 16010^6 Гн, E = 100 В, C = 16010^12 Ф. Найти токи и напряжения после замыкания ключа.

Решение. 1.Найдем характеристи­ческое уравнение

,

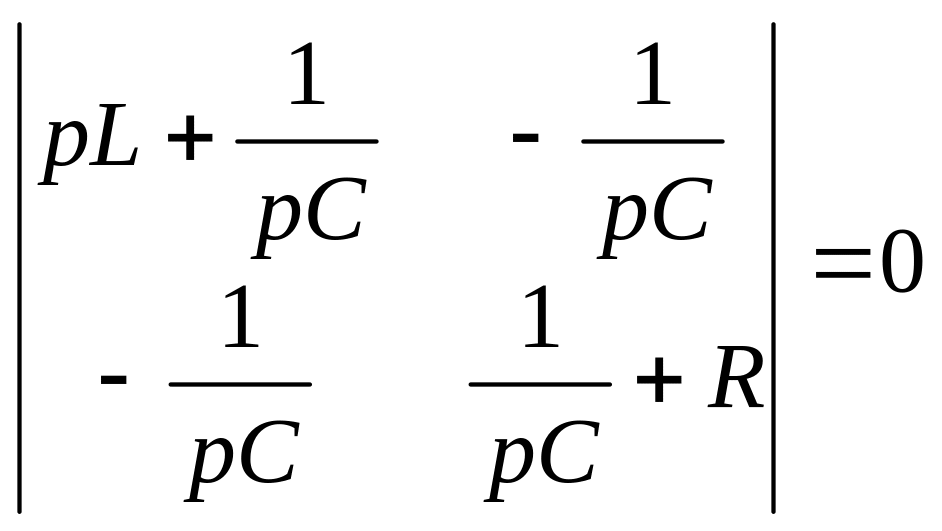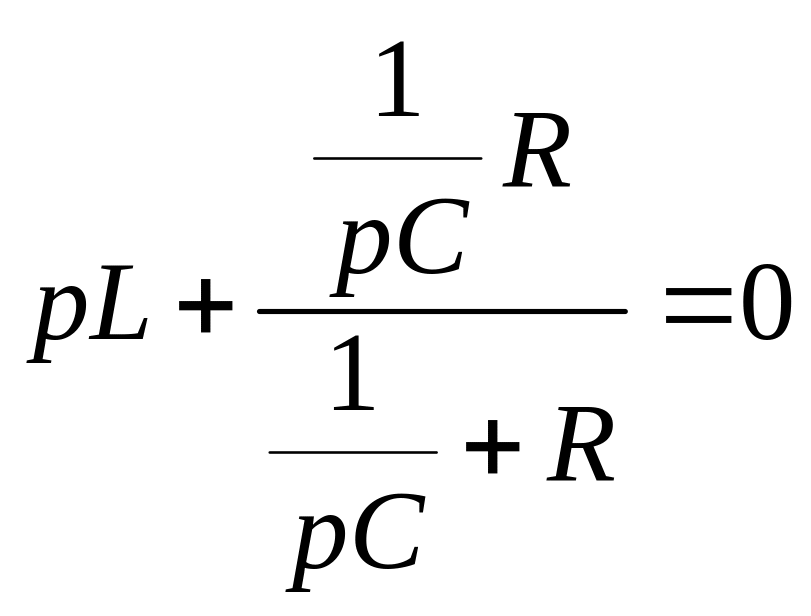, откуда .

Корни характеристического уравнения

,

, . (4.3.5)

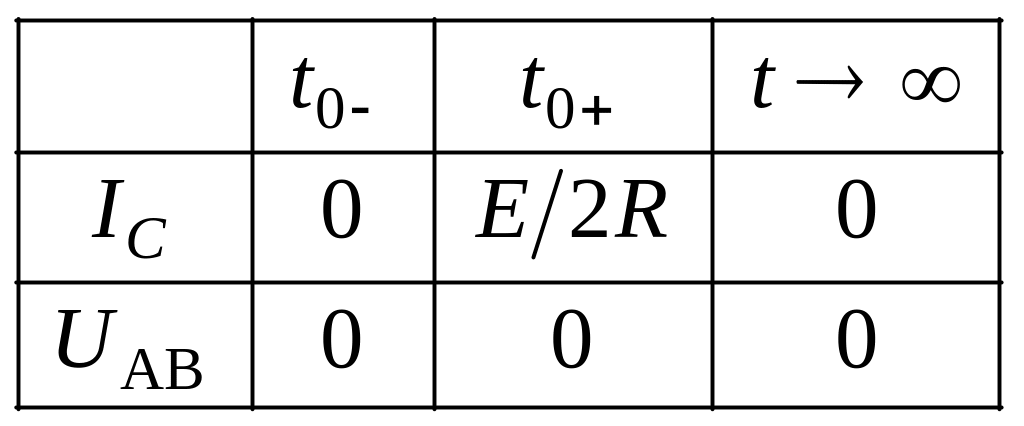
2. Составим таблицу начальных условий:

3. В общем виде решение для токов и напряжений:

. (4.3.6)

Однако так как корни характеристического уравнения комплексно сопряжены, сопряжены не только p₁ и p₂, но и коэффициенты A₁ и A₂; в результате решение можно представить как

.

4. Найдем напряжение и ток конденсатора:

; (4.3.7)

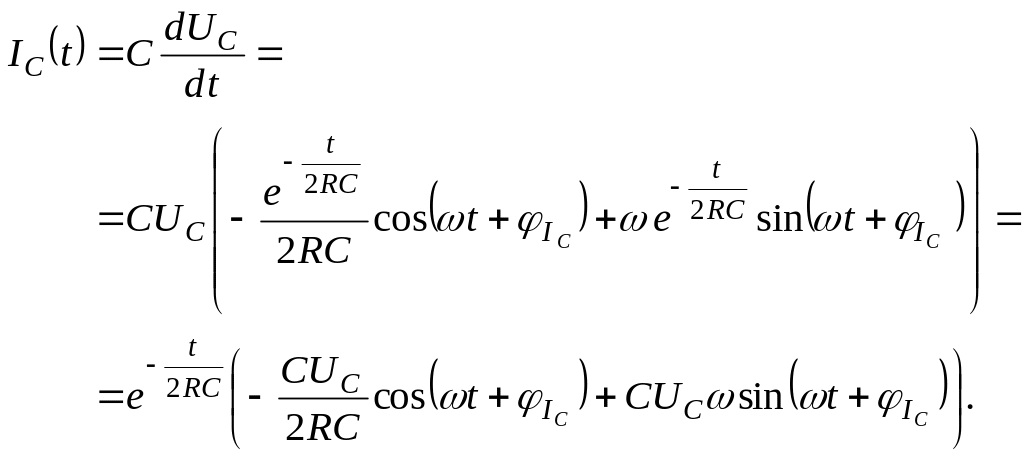_(4.3.8)

Решим уравнение (4.3.8) для момента t = 0₊:

;

;

; .

Решим уравнение (4.3.7) для момента :

, откуда .

Окончательно напряжение на емкости:

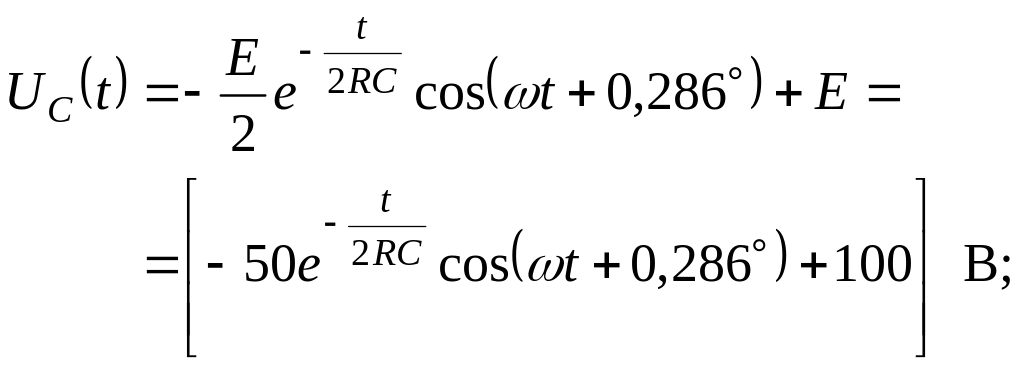
Ток через емкость:

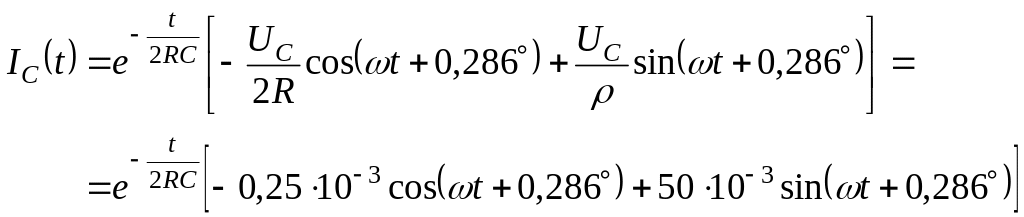 _A.

Ток через резистор R₂:

Ток индуктивности I_L можно найти из уравнения Кирхгофа:

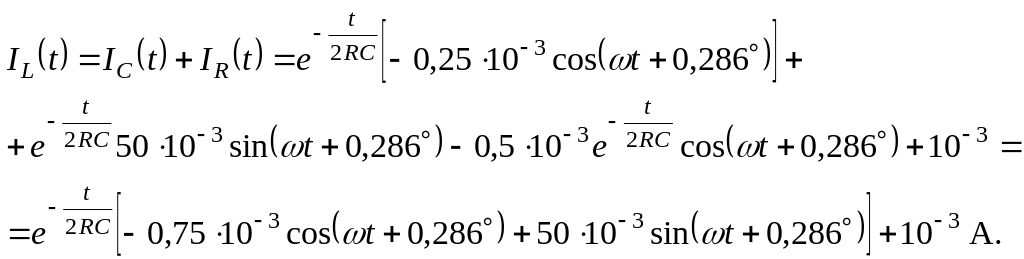
Напряжение на индуктивности так же найдем из уравнения Кирхгофа:

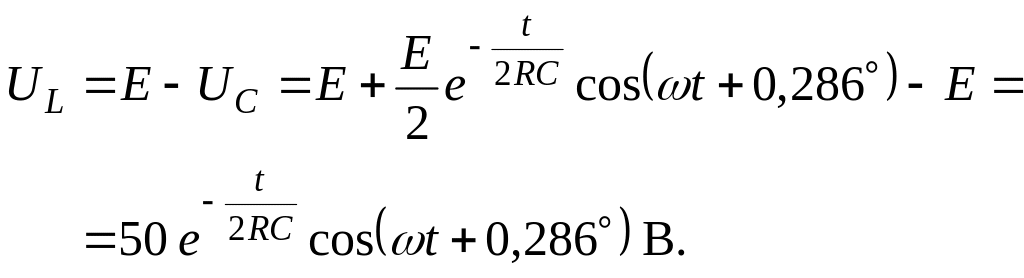
На рис. 4.3.5а и 4.3.5б представлены в качестве приме­ра графики переходных процес­сов напряжений на катушке индуктивности и на конден­саторе (здесь и далее графики получены с помощью модели­рующей программы Work Bench).

Рис. 3.4.5а

Рис. 3.4.5б

Рис. 4.3.6

Задача 4.3.3 (для само­сто­я­тельного решения). На рис. 4.3.6 изображена схема фильтра, назы­ваемого мостом Вина. Найти напряжение U_AB при переклю­че­нии ключа из положения 1 в положение 2. Изобразить график переходного процесса.