Вопрос 1 Случайное событие. Определение вероятности (статистическое и классическое)
Виды событий: случайное, достоверное, невозможное.
Случайное событие - это факт, который в результате испытания может произойти или не произойти.
Вероятность случайного события - это численная мера объективной возможности наступления этого события.
Классическое
определение вероятности:
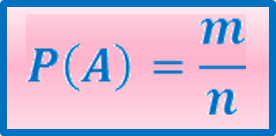
Вероятность события А- отношение числа случаев, благоприятствующих событию А (m), к общему числу случаев. (n)
Классическое определение вероятности основано на понятии равновозможности исходов. Например, вероятность выпадения «орла» или «решки» при случайном подбрасывании монетки равна 1/2, если предполагается, что только эти две возможности имеют место и они являются равновозможными.
Статистическое определение вероятности.
Вероятность события- число, относительно которого группируются значения частоты данного события в различных сериях большого числа испытаний
Относительная частота события- это доля тех фактически проведенных испытаний, в которых событие А появилось.
Это опытная экспериментальная характеристика, где m- число опытов, в которых появилось событие А; n- число всех проведенных опытов.
Если классическое определение вероятности осуществляется до опыта, то статистическое после опыта по результатам.
Вопрос 2 Понятие о совместных и несовместных событиях, зависимых и независимых.
Случайные события А1, А2,..Аn называются:
Совместные - если появление одного из них не исключает появления другого в одном и том же испытании.
Несовместные - если наступление одного события исключает появление другого.
Зависимое событие: вероятность появления одного из них зависит от появления другого.
Независимое событие: если вероятность появления одного из них не зависит от появления или не появления другого.
Условная вероятность события B- вероятность события B, найденная при условии, что событие A произошло. P(B/A)
Вопрос 3 Теоремы умножения и сложения вероятностей.
Сумма двух событий- это такое событие, при котором происходит хотя бы одно из этих событий (А или В).
Вероятность суммы:
Несовместных событий означает наступление или события А или события В и равна сумме вероятностей этих событий: P(A+B)= P(A) + P(B).
Совместных событий обозначает наступление события А или события В, или обоих событий вместе и равна сумме вероятностей этих событий без вероятности их совместного появления: P(A+B)= P(A) + P(B) – P(AB)
Теорема умножения вероятностей.
Произведение двух событий- это событие, состоящее в совместном появлении этих событий (А и В).
Вероятность совместного появления:
Независимых событий равна произведению вероятностей появления каждого из них: P(A*B)=P(A)*P(B)
Зависимых событий: P(A*B)=P(A)*P(B/A)
Вопрос 4 Распределение дискретных и непрерывных случайных величин. Их характеристики: математическое ожидание, дисперсия, среднее квадратическое отклонение.
Случайная величина - это величина, которая в результате испытания примет одно и только одно возможное значение заранее неизвестное.
Случайные величины: дискретные (счет: 1-2-3..) и непрерывные (измерения: Амперы, Вольты..)
Дискретная случайная величина- случайная величина, когда принимает отдельное изолированное, счетное множество значений.
Непрерывная случайная величина- случайная величина, принимающая любые значения из некоторого интервала.
Распределение = закон распределения - это совокупность значений случайной величины и вероятностей их появления.
Способы задания величин: табличный (дискретные), аналитический, графический.
Характеристики:
Математическое ожидание - сумма произведений случайных величин на вероятность их появления.
Для дискретных случайных величин: а)
Для непрерывных случайных величин: б)
а)
б)
Дисперсия - рассеяние вокруг математического ожидания.
Для
дискретных случайных величин:
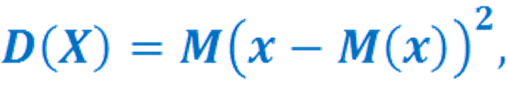
Для непрерывных случайных величин:
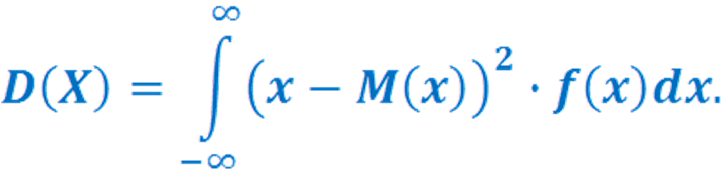
Среднее
квадратическое отклонение случайной
величины-
корень квадратичный из дисперсии.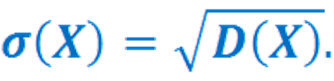
Стандартное
отклонение
