
Формула Пуанкаре.
Предположим дополнительно, что кривая Γ (x = x(t), y = y(t), a ≤ t ≤ b) кусочно-гладкая, а векторное поле
Φ(x,y) = (φ(x,y),ψ(x,y))
непрерывно дифференцируемо в том смысле, что функции φ(x,y) и ψ(x,y) непрерывно дифференцируемы.
Пустьвектор
Φ(t) = (φ(x(t),y(t)),ψ(x(t),y(t)))
образуетсосьюабсциссуголα(t).Очевидно,
θ(t) = α(t) − α(a)
и
dθ
= dα
= darctg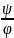 =
=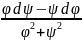 .
(1.14)
.
(1.14)
Отсюда вытекает, что
γ(Φ,Γ)
=
(θ(b)
− θ(a))
=
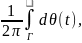
то есть
γ(Φ,Γ)
=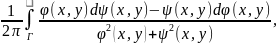 (1.15)
(1.15)
Эта формула имеет смысл, так как знаменатель в подынтегральном выражении в нуль не обращается — вращение (как и угловая функция) определено лишь для непрерывных полей без нулевых векторов.
Если положить
φ(x(t),y(t)) = φ(t), ψ(x(t),y(t)) = ψ(t),
то формулу Пуанкаре (1.15) можно записать при помощи обыкновенного интеграла
γ(Φ,Γ)
= dt.(1.16)
dt.(1.16)
Для фактического вычисления вращения формула Пуанкаре малоудобна.
Вычисление вращения.
После введения параметра вычисление вращения поля на произвольной кривой сводится к вычислению вращения поля
Φ(t) = (P(t),Q(t))(1.17)
на
некотором отрезке x
= t, y = 0 (a ≤ t ≤ b).
При вычислении вращения удобно отрезок
[a,b] разбить на части так, чтобы вращение
на каждой части вычислялось просто, а
затем воспользоваться тем фактом, что
вращение на всем отрезке равно сумме
вращений на его частях. При вычислении
вращения полезно иметь в виду, что
вращение равно выраженному в единицах
полного оборота наименьшему углу между
векторами на концах кривой ,
если ни один вектор поля Φ(M) не направлен
противоположно вектору Φ(
,
если ни один вектор поля Φ(M) не направлен
противоположно вектору Φ(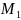 )
в точке
(если ни один вектор поля не направлен
противоположно вектору Φ(
)
в точке
(если ни один вектор поля не направлен
противоположно вектору Φ(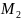 )
в точке
).
Для доказательства достаточно заметить,
что в общем случае вращение отличается
от угла между векторами Φ(
)
и Φ(
)
на целое число и что угловая функция
поля, вращение которого по абсолютной
величине больше ½ , принимает либо
значение π, либо значение −π (в
соответствующей точке вектор поля
направлен противоположно Φ(
)).
Допустим, что уравнение
)
в точке
).
Для доказательства достаточно заметить,
что в общем случае вращение отличается
от угла между векторами Φ(
)
и Φ(
)
на целое число и что угловая функция
поля, вращение которого по абсолютной
величине больше ½ , принимает либо
значение π, либо значение −π (в
соответствующей точке вектор поля
направлен противоположно Φ(
)).
Допустим, что уравнение
P(t) = 0 (1.18)
имеет на [a,b] конечное число решений
 <
<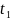 <
... <
<
... < .
.
Вращение γ поля (1.17) на всем отрезке [a,b] представим как сумму
γ
=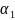 +
+
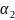 +
+ +
... +
+
... +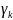 ,
(1.19)
,
(1.19)
где
 — вращения соответственно на отрезках
[
— вращения соответственно на отрезках
[ ,
]
и [
,b],
а
— вращение на отрезке [
,
]
и [
,b],
а
— вращение на отрезке [ ,
,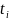 ]
(i
= 1,...,k).
]
(i
= 1,...,k).
На
каждом отрезке [
,
]
колебание угловой функции θ(t) поля
(1.17) не превышает π, так как в противном
случае функция P(t) принимала бы нулевое
значение в некоторой точке интервала
(
,
).
Поэтому каждое
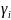 принимает
одно из трех значений: ½,0,− ½ .
принимает
одно из трех значений: ½,0,− ½ .
Если
signQ( ) = signQ( ),
то векторы поля на концах отрезка [ , ] направлены одинаково и поэтому = 0.
Пусть
signQ( ) = 1, signQ( ) = −1.
Тогда
(см. рис. 1.4)
= −½при P (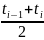 )
> 0 и
= ½при P(
)
< 0.
)
> 0 и
= ½при P(
)
< 0.
Аналогично при
signQ( ) = −1, signQ( ) = 1
вращение γi вычисляется по правилу = −½при P ( ) < 0 и = ½при P( ) >0.
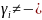

 ½
½
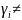 ½
½
P(t)>0 P(t)<0
Рис. 1.4
Все перечисленные случаи можно охватить общей формулой
=
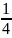 signP(
)(signQ(
)
− signQ(
)),
(1.20)
signP(
)(signQ(
)
− signQ(
)),
(1.20)
проверкукоторойпредоставляемчитателю. Формула (1.19) перепишетсятогдаввиде
γ = + + signP( )(signQ( ) − signQ( )). (1.21)
При
применении этой формулы полезно помнить,
что P(t) на интервале ( )
принимает значения одного знака. В
качестве примера рассмотрим поле
)
принимает значения одного знака. В
качестве примера рассмотрим поле
Φ(x,y)
= ( −
−
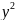 ,10xy)
,10xy)
на той половине единичной окружности, которая выделена неравенством y ≥ 0, с параметром t = x. Функции P(t) и Q(t) определяются равенствами
P(t)
= 2 −
1, Q(t) = 10t
−
1, Q(t) = 10t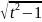 (−1 ≤ t ≤ 1).
(−1 ≤ t ≤ 1).
Уравнение
P(t) = 0 имеет два корня:
= −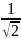 ,
=
.
Направление векторов Φ(−1) и Φ(1) совпадает
с положительным направлением оси
абсцисс. Векторы Φ(
)
и Φ(
)
направлены соответственно по отрицательному
и положительному направлению оси
ординат. Поэтому
=
= −
. Из формулы (1.21) вытекает, что вращение
рассматриваемого поля равно −1.
,
=
.
Направление векторов Φ(−1) и Φ(1) совпадает
с положительным направлением оси
абсцисс. Векторы Φ(
)
и Φ(
)
направлены соответственно по отрицательному
и положительному направлению оси
ординат. Поэтому
=
= −
. Из формулы (1.21) вытекает, что вращение
рассматриваемого поля равно −1.
Нетрудно видеть, что формула (1.21) сохраняет силу, если сумму в ней брать только по таким парам соседних нулей функции P(t), между которыми есть нули функции Q(t). В этой последней форме формула (1.21) верна и в том случае, когда уравнение P(t) = 0 имеет бесконечное множество нулей.
Некоторые свойства вращения .
1. При изменении ориентации линии L на противоположную значение g(L; А) умножается на -1.
2. Если линия L разбита на несколько частей, ориентированных в соответствии с ориентацией L, то вращение поля вдоль L равно сумме его вращений вдоль всех частей.
3. Если линия L замкнутая, то g(L; А) - целое число, не зависящее от того, какая точка на L была принята за начальную.
4. Если замкнутая линия L непрерывно деформируется так, что в любой момент процесса деформации она не проходит через особые точки поля, то вращение поля вдоль деформируемой линии остается неизменным.
5. Если на замкнутой линии L и внутри нее нет особых точек поля А, то g(L; А) = 0.
