МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ

ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО

ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ УНИВЕРСИТЕТ»

КАФЕДРА ВЫСШЕЙ МАТЕМАТИКИ

Курсовая работа

На тему: «Вращение векторного поля. Примеры».

Выполнила: студентка 1 курса магистратуры направления «Педагогическое образование» программа подготовки «Математическое образование»

физико-математического факультета

Шпак И. С.

Научный руководитель:

кандидат физико-математических наук,доцент кафедры высшей математики

Корнев С.В.

Воронеж 2014г.

СОДЕРЖАНИЕ

Введение

1. Вращение векторного поля

   1. Векторное поле

   2. Угловая функция

   3. Вращение поля

   4. Формула Пуанкаре

   5. Вычисление вращения

2. Примеры вращения векторного поля

   1. Дивергенция векторного поля

   2. Циркуляция

   3. Ротор и его основные свойства

3. Формулы Грина

4. Формулы Стокса

Заключение

Литература

Введение

Векторный анализ - это раздел векторного исчисления, в котором изучается средствами математического анализа векторные и скалярные функции одного или нескольких аргументов (векторные поля и скалярные поля). Для характеристики данных полей вводится целый ряд понятий, часть которых приведены в данной работе: вращение векторного поля, циркуляция, дивергенция, ротор.

Поле - область пространства, каждой точке которого соответствует определенное значение некоторой физической величины. По своему характеру физические величины могут быть скалярными или векторными. Соответственно поля этих величин также являются скалярными или векторными. Так же в данной работе будут приведены формулы британского математика и физика Джорджа Грина и английского физика-теоретика и математика ирландского происхождения Джорджа Габрие́ля Стокса. Объектом исследования в курсовой работе являются процессы поведения характеристик векторного поля.

Цель написания работы состоит в изучении теории поля с помощью векторного анализа, и закрепить полученные знания по высшей математике.

1. Вращение векторного поля

   1. Векторное поле.

Пусть в каждой точке M некоторого плоского множества Ω задан вектор Φ(M), лежащий в той же плоскости. В этом случае будем говорить, что на Ω задано векторное поле Φ. Если на плоскости определена некоторая прямоугольная система координат, то задание векторного поля Φ(M) эквивалентно заданию двух вещественных функций φ(M) и ψ(M) точки M ∈ Ω — компонент векторов Φ(M).

Векторное поле будем называть непрерывным, если функции φ(M), ψ(M) непрерывны.

Векторные поля встречаются и их приходится изучать при решении разнообразных математических задач.

В частности, во многих случаях векторы Φ(M) определяются как сдвиги точек, определяемые некоторым преобразованием A, заданным на Ω:

Φ(M) = A(M) − M.

В качестве второго примера рассмотрим систему дифференциальных уравнений

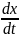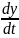= P(x,y), = Q(x,y). (1.1)

Если решение этой системы рассматривать как закон движения точки в плоскости с прямоугольными координатами (x,y), то векторное поле

Φ(x,y) = (P(x,y),Q(x,y))(1.2)

— это поле скоростей движущихся по упомянутым законам точек. Выписать решения системы (1.1) в явном виде обычно невозможно, а общее представление о поле скоростей (1.2) в ряде случаев можно получить без труда. Априори ясно, что общие характеристики поля скоростей должны нести существенную информацию о решениях системы (1.1).

Рассмотрим, наконец, функцию f(z) комплексного переменного z = x + iy. Изучение функции

f(z) = u(x,y) + iv(x,y) (1.3)

равносильно изучению векторного поля

Φ(x,y) = (u(x,y),v(x,y)).(1.4)