2.9 Сурет

Белгіні жіберу кезінде байланыс өзгермес үшін, 2.9 суретте көрсетілгендей фиктивті буынның 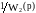өткізетін функциясын енгізу керек.

Күрделі жағдайларда өзгерту процессінде арнайы есеп жүргізу керек.

б)

Сурет 2.10

Үлкендіктер арасында байланыс құрайық және .

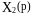На входе звеньев с передаточными функциями 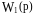и действует сигнал

Өтпелі функцияның шығарылымы

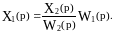
Тораптық1 сумматордың шығуы

Осы жерден біз көре аламыз, қарастырылып отырған мысалда торапты орнынан қозғаған кезде ол жерге жалған түйінді функцияны қоямыз 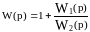, 2.10 суретте көрсетілгендей

Түйіннің схемасын орнынан қозғаған кезде сурет 2.11,ал сумматордың шығуы оның жақсы кіруінің біз жалған функцияның артық түсіндіруінсіз ақ таба аламыз.

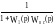
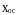
а) б)

Рис.2.11

Үлгі звеношы және оның сипаттамасы

Жалпы алған да автоматтық жерде басқару берілетін функция арқылы анықталады, құрамындағы полиномдар р дан бастап сандық және бөлгіш реттігімен жазылады. Бірақ егер жай берілетін функция өзінің құрамында тек қана жай сандықтағы көпшіктен құралатын болса (бөлгіш осы мен қоса өзінің құрамын да анықталған сандықты қосады) немесе жай ғана бөлгіштегі көбейткіш (есептегіш өзінде анықталған сандарды көрсетеді), онда осы объект үлгілі динамикалық бөлшек деп аталатын болады (немесе жай ғана бөлшек үлгісі).

Алгебраның курсын білетін болсақ бізге мыналар белгілі болады, әр реттіктің полиномын жай көбейткіштерге жіктеуге болады деген. Онда барлық САУды бөлшектің дәйекті түрде типтардың қосылуы деп айтта аламыз. Басқа жақтан қарағанда САУдың бөлшектері әр түрлі физикалық негіз құрай алады (электронды, механикалық, гидравликалық, электромеханикалық және тағыда сол сияқты) және конструкталық орындалу , бірақ өзде бірдей өтпелі функциясы болады және де бірдей типтік бөлшектті болады. Сондықтан да бөлшектің мінездемесін білу өте маңызды және ол САУ үшін де керек етеді, арифметикадағы көбейту кестесін білу секілді керек етеді.

Барлық типтік сызықтық бөлшектер үш группаңа бөлінеді: позициалдық бөлгіш, интегралдық және дифференциалдық. Позициалдық бөлгіш : қайталанбайтын, қарамақарсы, ауыспалы, кертапталық және анық кешігу – кертапталықтан басқасында әр қайсысында шығудың өсуінде уақыттың өтуінде тұрақты өсулік пайда болады.

Бөлгіште, интегралдық группаға жатады, әр шығу кезінде шығу үлкендігі сансыз өседі.

Дифференциалдық бөлгішті біз мына мен мінездей аламыз, ол тек қана кірістің өсуіне ғана мән береді.

Типттік бөлшекті және оның мінездемесін қарастырайық.

Қарама қарсы түйін.

Тендік және берілу функциясы көрсетілет :

K параметрі көп жерлерде бөлшектің коэффциентінің берілетіні деп аталады және кез келген көлем қабылдай алады. Соның ішінде k үлкендіктің өлшемсіз болады, «өсу коэффциенті» деп атау жақсы естіледі.

Таза және бөлшектік функцияның бөлшегі:

.

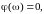
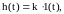
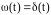Осындай механикалық бөлшектің мысалына біз, электірлік күшейткіш төменгі частотада және басқа да сол сияқты.

Сурет 2.6, б схемасы, егер и 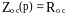, және сол секілді қарама қарсы түйін болады.

Интегралдық түйін .

Интеграл және берілу функциясының бөлшегі:

или

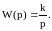
Интегралды бөлшектің параметрі k коэффциенті жылдамдық түйіні болады, Шығудың өзгерсітік санының өзгеруі кіріс өлшемінің өсуіне сәйкес келеді.

Жиілік және уақыттық функцияның бөлшегі:

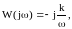
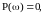
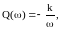
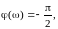
Құрастырылған функцияның мінездемесі 2.12. суретте көрсетілген.

ЛАЧХны құру кезінде координата нүктесін қоя тұрған ыңғайырылақ болады ( ); және тіке көлбеуді жүргізу 20 дБ/дек, әр жиілікті бір декадаға көбейткен сайын оның ЛАЧХ ординатасы 20 дБ төмендей береді. ( кез келген мағынасында 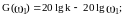аламыз, жиілікті бір декадаға көбейткен кезде , яғни 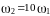болғанда, соған орай 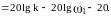Бұл ординаталардың әр түрлігі өзінде 20 дБ минусынан тұрады .)

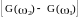Элементтің мысалы ретінде, Интегралдық бөлшектің мінездемесінің ең жақсы мінездемесіне сәйкес келетін, оны біз электр энергияның тоқтаусыз қозғалтқышының бастамасының және кіші электромеханикалық инерция деп атай аламыз. Кіру өсімділігі ол үшін якордің қысу куші болады, ал шығу – бұрыштың айналу білігі болып табылады.

Суреттің .2.6, б схемасы , интегралдық түйін болады, 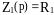, ал темір кері байланыс конденсаторо, яғни

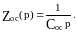
Шынында ол, (2.5) формуласына сай берілу функциясы осылай болады

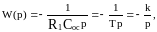
+j АФЧХ А()

0 +1

 0 

G()

20lgk 20дБ/дек

0 lg

lgk

()

h(t) (t)

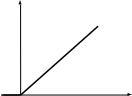
k

0 t t

Рис.2.12

Қарастырылып отырған схемаға қарай операциондық күшейткіш ауыспалы мінездемесі мағынасы бола алмайды, зарядтың кушінен көп жұмсай алмайды. Бірақ оперециондық кушейткішті ең жақсы деп алып қарастыратын болсақ , онда осы жерде орындалып отырған интенралдық бөлігіде соншалықты жақсы болады.