Логарифмдік жиілік өлшемдерінің элементар динамикалық звенолары

 

Инерциясыз звено

Табыстама функция –

.

Жиілік характеристика –

,

АЧХ и ФЧХ

.

Логарифмдык характеристикалар

 

Дифференциалданған звено

Табыстама функция –

.

Жиілік характеристика –

,

АЧХ и ФЧХ

.

Логарифмдік характеристика

Құрылыстың жайлылығы үшін нүктені анықтаймыз, ЛАЧХ жиілік белдігімен қиылысқан жерде –

.

Қисықтықты анықтаймыз ЛАЧХ

,

ана бол-, аламыз, не ЛАЧХ 20 децибелдің приращение жиіліктің ара қашықтығында 1 онкүндікте алады.

 

Интеграцияланған звено

Табыстама функция –

.

Жиілік характеристика –

,

АЧХ и ФЧХ

.

Логарифмдік характеристикалар

Құрылыстың жайлылығы үшін нүктені анықтаймыз, ЛАЧХ жиілік белдігімен қиылысқан жерде частот –

.

Қисықтықты анықтаймыз ЛАЧХ

,

ана бол-, аламыз, не ЛАЧХ 20 децибелдің приращение жиіліктің ара қашықтығында 1 онкүндікте алады..

ДӘРІС №13

Статикалық сипаттамаларды коррекциялау

Іс жүзінде автоматты реттеу жүйесінде пайдаланылатын стандарт элементтердің статикалық сипаттамалары талапқа сай келмейтін жағдайлар кездеседі. Бұл жағдайда қажетті сипаттаманы алу үшін жүйеге арнайы қиылыстырылған статикалық сипаттамалары бар статикалық корректілуші (түзетуші) буындарды параллель, тізбектей немесе кері байланысбойынша қосуға болады.

Есепті шығару жолы жоғарыда келтірілген графикалық әдістер бойынша мына ретпен жүргізіледі:

Алдымен буынның бастыпқы сипаттамасы мен талапқа сай сипаттамасы салынады, содан кейін аралық буынның сипаттамасы табылады. Мысалы, параллель қосылуда 1 және 3 сипаттамалар (14-сурет) беріледі де, олардың айырымын алу арқылы 2 сипаттамасының ординатасы табылады.

Тізбектеле қосылуда I және IV сипаттамалар (13-сурет) беріледі, ал қосымша III сипаттама ретінде квадрант бұрышының биссектрисасы тұрғызылады да, белгілі әдіс бойынша II сипаттама салынады.

Коррекцияны кері байланыс бойынша жүргізгенде (15-сурет) 1 және 3 сипаттамалары беріледі де, 2 сипаттама анықталады.

Осылай тұрғызудың нәтижесінде корректирлеуші буынның талапқа сай сипаттамасы анықталып, осындай сипаттамалы буын құрылады.

Көптеген есептерді буынға үлкен к күшейту коэффициенті бар күшейткішті тізбектеп қосып, алынған тізбекті қайсыбір берілген статикалық сипаттамалы кері байланыспен қамтиды (19-cурет).

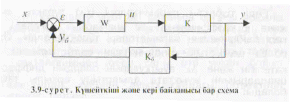
U = f(ε) – негізгі элементтің сипаттамасы, мұнда f(0) = 0, ал у_б = f(y) – кері байланыстағы буынның сипаттамасы делік. Теріс кері байланыс үшін

х = у_б + ε = f(y) +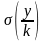 (33)

мұндағы f(ε) сипаттамасына кері сипаттама, мұнда .

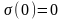Әрі қарай мүшесін еске алмай-ақ қоюға болатындай к күшейту коэффициентін таңдап аламыз. Онда

(34)

яғни мұнда схемадағы статикалық сипаттама, кері байланыстың кері статикалық сипаттамасына үлкен дәлдікпен сәйкес келеді.

19- суреттегі схема құрылғының дәлдігін жоғарылату үшін де қолданылады. Күшейткіштің жеткілікті үлкен к күшейту коэффициентінде схеманың қателігі кері байланыс тізбегіндегі элементтің қателігімен анықталады. Сондықтан прецизиондық схеманы (19-сурет) алу үшін сипаттамалыра дәл емес буын мен күшейткішке прецизиондық кері байланысты қосса жеткілікті. Беріліс коэффициенті к тізбекті к_б коэффициентті теріс кері байланыспен қамтыса

(35)

Енді тізбектің параметрлері (f,k) тұрақты емес және к коэффициенті ∆к шамасына өзгереді, ал кері байланыстың параметрлері тұрақты делік. Олай болса, шығыстық координаттың салыстырмалы ∆у қателігін және ∆к ауытқуларын олардың дифференциалдарымен жуықтата алмастыру арқылы табуға болады:

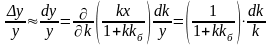(36)

Сонымен, кері байланысты енгізу салыстырмалы қателікті негізгі тізбектің параметрлерінің шашырауынан 1+кк_б есе азайтады.

Енді сызықтық тұйықталған жүйенің статикалық сипаттамасын қарастырайық. Бұл жағдайда объектінің статикасының:

у = к₀х – к₁f (37)

реттеуіштің ауытқу және жүктеме f бойынша статикасының :

х₁ = -к_ру, х₂ = к_ж f (38)

реттеуіштің реттеуші органмен байланысының:

х = х₁+ х₂=-к_ру+ к_ж f (39)

теңдеулері берілген делік.

Ауытқу бойынша әсердегі минус белгісі ауытқу бойынша кері байланыстың теріс екенін көрсетеді.

(37) - (39) өрнектерінен х шамасын шығарып тастап, реттелетін у шаманың f жүктемеден тәуелділігін анықтайық:

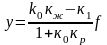(40)

Тек ауытқу бойынша жұмыс істейтін реттеуіш үшін, к_ж = 0 онда

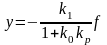(41)

ДӘРІС №14

Бірнеше реттелуші шамалары бар сызықты жүйенің статикасы

Есепті жеңілдету үшін екі реттеуші органы арқылы басқарылатын және екі жүктемеден тәуелді, екі реттелетін шамамен сипатталатын реттеу объектісін қарастырайық. Айнымалылар саны көп болса, талдау әдісі сақталғанымен есеп саны өте үлкен болып кетеді.

Тепе- теңдік күйінен ауытқығандағы объектінің статикалық теңдеуі

(42)

мұндағы х – реттелетін шамалардың ауытқуы;

у – реттелетін органның ауытқуы;

f – жүктемелердің өзгеруі.

Ауытқуы және жүктемесі бойынша жұмыс істейтін аралас әрекетті реттеуішті қарастырайық. Реттеуіштің статикалық теңдеулері

(43)

Реттеуіштің реттеуші органмен c_ij ауытқуы бойынша және d_ij жүктеме бойынша байланыс коэффициенттерін координаттардың бір-бірімен (статикалық дербестілік шарты) және орныққан мәндерінде жктемелерден (статикалық инварианттық шарты) тәуелсіздіктерін қанағаттандыратындай етіп таңдау мәселесін алға қояйық.

f₁ және f₂ жүктемелері бойынша y₁ және y₂ координаттарының дербес туындыларын нөлге теңеу арқылы толық статикалық инварианттылықтың шартын аламыз:

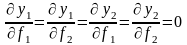(44)

(43) формуласын f₁ және f₂ бойынша дифференциалдап және (44) өрнегін ескере отыра, аламыз:

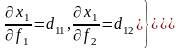(45)

(42) теңдеуін алдымен f₁, соңынан f₂ бойынша дифференциалдап және (45) өрнегін ескере отыра:

(46)

(46) теңдеуін d₁₁, d₁₂, d₂₁, d₂₂ сәйкес шешелік:

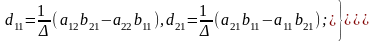(47)

мұндағы ∆= a₁₁a₂₂ – a₁₂a₂₁.

Дербестік шарты дегеніміз y1 және y2 координаттарының бір-бірінен тәуелсіздігі. Оны бір координаттың екінші координаттан дербес туындысын нөлге теңеу арқылы алуға болады, яғни

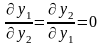(48)

(43) теңдеуін y₁ және y₂ бойынша дифференциалдап және (48) өрнегін ескере отыра:

(49)

(42) теңдеуін алдымен y₁, соңынан y₂ бойынша дифференциалдап және (49) өрнегін ескере отырып, төрт теңдеу аламыз:

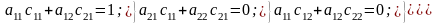(50)

Бұл теңдеулерді с₁₁, с₁₂, с₂₁, с₂₂ сәйкес шеше отыра, мына өрнекті аламыз:

(51)

(47) және (51) өрнектерін қарастыра отыра мынандай шешім жасауға болады:

статикалық дербестік шарты b және d коэффициенттерінен тәуелді емес, ол тек ауытқу бойынша әрекетті реттеуішті жөндеп күйге келтіру жолымен қамтамасыз етіледі. Түсінікті болу үшін: b коэффициенті жүктеменің реттелетін шамаларға әсер ету дәрежесін анықтайтын коэффициент, ал d – реттеу тізбегіндегі жүктемелер бойынша әсерлер коэффициенті. Статикалық инварианттық шарты b және d коэффициенттеріне тәуелді және тек жүктеме бойынша әрекеттенетін реттеуіштермен қамтамасыз етіледі. Ауытқу және жүктеме бойынша жұмыс істейтін аралас әрекетті реттеуішті сәйкестікпен жөндеп күйге келтіру арқылы дербестік пен инварианттықтың бірмезгілде орындалу шартын алуға болады.

ДӘРІС №15