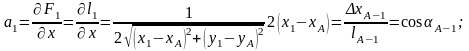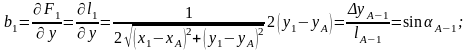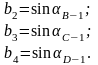Триангуляциялық торға өлшенген ара қашықтықтар бойынша пункты орналастыру (өлшемшарттық әдіспен)

1. Есептің берілгені

3.1 суретіне сәйкес өлшенген ара қашықтықтар бойынша бар триангуляциялық торға пункті орналастыру кезіндегі теңдеулік есептеулерді орындау. А, В, С және D бекітілген пункттердің координаттары орналастырылатын 1 пункттың жуықталған координаттары және өлшенген ара қашықтықтар 3.1 кестесінде келтірілген.

3.1. кестесі Есепті шығару үшін арналған бастапқы шарттар

Пункт атаулары	Пункт координаталары, м		Жақтар Атауы	Өлшенген арақашықтық li, м
	X	Y
А В С D	+2866,176 +2733,856 +5315,704 +4572,691	-3208,680 -5284,786 -1934,758 -5173,405	А-1 В-1 С-1 D-1	654,52 1992,91 2372,19 2051,07

3.1- Сурет Өлшенген ара қашықтықтар бойынша пункті

Орналастыру схемасы

А

C

, В, С және D нүктелері ертеректе құрылған триангуляциялық тордың пункттары, яғни қатты нүктелер, ал 1 нүктесі енгізілетін нүкте болып табылады. Енгізілетін нүктенің Х₁ және У₁ координаттарының теңестірілген мәндерін табу керек.

Ол үшін алдымен екі АВ1 және СD1үшбұрышттарын шығару арқылы алынатын 1 енгізілетін пункттың координаттарының жуықталған мәндерін есептеу қажет.

I. СD1 қарастыралық (3.2 - сурет).

1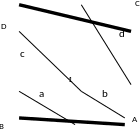 .1. СД (_СД) бағытының дирекциондық бұрышын анықтау керек:

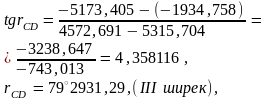
3.2 – сурет Үшбұрыштар схемасы

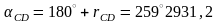
1.2. СД жағының ұзындығын анықтау керек:

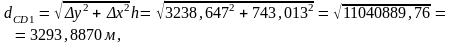
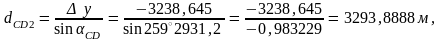
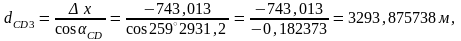
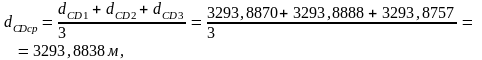
1.3. D және С төбелеріндегі бұрыштар есептеледі, ол үшін СD1 жартылай периметрін анықтау керек:

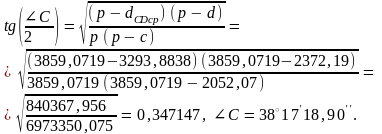
1.4. Координаттар бойынша құрылған схемаға сәйкес С-1 және D-1, жақтарының дирекциондық бұрыштарын есептеледі:

1.5. С-1 және D-1бағыттары бойынша координаттар өсімшелерін есептеу керек:

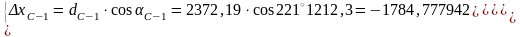
1.6. С және D пункттарына қатысты 1 енгізілетін нүктенің координаттарын екі рет есептеледі:

1.7. СD1 қатысты 1 пункттың жуықталған координаттары:

Х^/ ₁ = 3530,926058 м, Y^/ ₁ = -3497,402441 м.

II. АВ1 қарастырылық (3.2 – суретын қараныз).

3.1. АВ (_АВ) бағытының дирекциондық бұрышы анықталады:

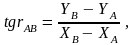
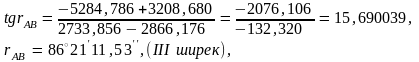
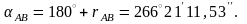
3.2. АВ жағының ұзындығын анықтау керек:

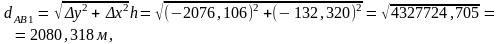
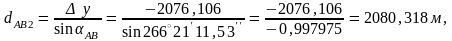
3.3. А және В төбелеріндегі бұрыштар есептеледі, ол үшін АВ1жартылай периметірін анықтау керек:

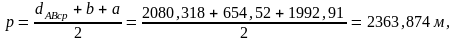
3.4. Координаттар бойынша схемаға сәйкес А-1 және В-1, жақтарының дирекциондық бұрыштары есептеледі:

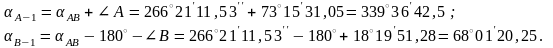
3.5. А-1 және В-1 бағыттары бойынша координаттарының өсімшелерін есептеледі:

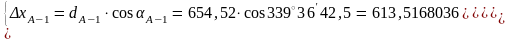
3.6. А және В пункттарына қатысты 1 енгізілетін нүктенін жуықталған координаттары, екі рет есептеледі:

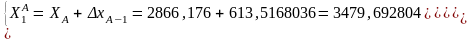
3.7. АВ1 қатысты 1 пункттың жуықталған координаттары:

Х^// ₁ = 3479,692804 м, Y^// ₁ = -3436,7010 м.

АВ1 және СD1 екі үшбұрыштарын шығару арқылы алынған 1енгізілетін пункттың жуықталған мәндері:

Х₁ = 3479,688 м, Y₁ = -3436,7016м.

А4 бетінде 1:25000 масштабында бар триангуляциялық торға 1 пунктты енгізу планын құру керек.

2 Түзетпелер теңдеулерін жалпы және сызықтық түрінде құрамыз

Егер берілген А, В, С, D пунктерінің координаттары және орналастырылатын 1 пунктері негізгі деп алсақ, онда А-1, В-1, С-1 және D-1 негізгі ара қашықтары орналастыратын пунктың координаттары арқылы өрнектеуге болады және олар мына түрде болады:

L₁=F₁(X₁, Y₁); L₂=F₂(X₁, Y₁);

L₃=F₃(X₁, Y₁); L₄=F₄(X₁, Y₁). (3.1)

Теңдеудегі (3.1) Х₁, Y₁ дәл координаттардың белгісіз мағыналардың орнына жуықтас мағыналарды х₁, y₁ қояйық, және өлшенген ұзындықтардың мағыналарын аламыз:

F₁(X₁,Y₁)-l₁=w₁;

F₂(X₁,Y₁)-l₂=w₂; (3.2)

F₃(X₁,Y₁)-l₃=w₃;

F₄(X₁,Y₁)-l₄=w₄.,

мұндағы w₁, w₂, w₃, w₄ – негізгі шамаларды жуықталғандармен алмастыру кезіндегі алынатын қиыспаушылықтар, ℓ₁, ℓ₂,, ℓ₃,, ℓ₄ – орналастыратын пункте дейін өлшенген ара қашықтықар; F(X₁, Y₁) – орналастыратын пункте жуықтылған ара қашықтықтар. Олар келесі турде анықталады:

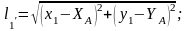
(3.3)

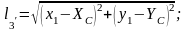
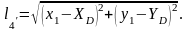
Орналастырылатын пункттың координаталарының жуықталған мәндеріне δ_x және δ_y, түзетпелерін енгіземіз. Онда (3.2) теңдеуінің бірінші белігіндегі қиыспаушылықтар ауысады және олар V_i деп белгілейміз:

F₁(x₁+δ_x, y₁+δ_y)-l₁=V₁;

F₂(x₁+δ_x, y₁+δ_y)-l₂=V₂; (3.4)

F₃(x₁+δ_x, y₁+δ_y)-l₃=V₃;

F₄(x₁+δ_x, y₁+δ_y)-l₄=V₄ .

Алынған V_i қиыспаушылықтар ℓ_i өлшенген ұзындықтарға түзетпелер болып табылады (3.4) теңдеуін жалпы түрдегі түзетпелер теңдеуі деп аталады.

(3.4) теңдеуінің сол жағындағы функцияларды Тейлора қатарына жіктеп, бірінші қатардағы мүшелерімен шектеліп және функциялардың белгісіз аргументтері бойынша бірінші туындылары а_i, b_i, функциялармен коэффициенттерімен белгілеп, түзетпелер теңдеулер жүйесін сызықтық түрінде аламыз:

V₁=a₁ δ_x+b₁ δ_y+w₁;

V₂=a₂ δ_x+b₂ δ_y+w₂; (3.5)

V₃=a₃ δ_x+b₃ δ_y+w₃;

V₄=a₄ δ_x+b₄ δ_y+w₄ ,

мұндағы