
- •Сәулет-құрылыс факультеті
- •Орташа квадраттық қателіктерді анықтау, бірдей дәлдікті өлшемдер және өлшенген аргументтер функциялары
- •Дәлдігі бірдей емес өлшеулер дәлдігін бағалау
- •Триангуляциялық торға өлшенген ара қашықтықтар бойынша пункты орналастыру (өлшемшарттық әдіспен)
- •Орналастыру схемасы
- •3 Бекітілген пункттердегі орналастырылатынға дейін жақтардың жуықталған ұзындықтары мен түзетпелер теңдеуінің wi бос мүшелерін анықтау.
ҚАЗАҚСТАН РЕСПУБЛИКАСЫНЫҢ БІЛІМ ЖӘНЕ ҒЫЛЫМ
МИНИСТРЛІГІ
Л.Н. ГУМИЛЕВ атындағы ЕУРАЗИЯ ҰЛТТЫҚ УНИВЕРСИТЕТІ
Сәулет-құрылыс факультеті
Тақырыбы: «Құрылысты геодезиялық қамтамасыздандыру »
Қабылдаған: Дөненбаева Н.С.
Орындаған: ГК –23 тобының студенті
Кошербаева Айдана
Астана – 2013
МАЗМҰНЫ
№ 1 ТАПСЫРМА Орташа квадраттық қателіктерді анықтау, бірдей дәлдікті өлшемдер және өлшенген аргументтер функциялары |
|
|
№ 2 ТАПСЫРМА Дәлдігі бірдей емес өлшемдердің дәлдігін бағалау |
|
|
№ 3 ТАПСЫРМА Триангуляциялық торға өлшенген арақашықтықтар бойынша пункты орналастыру (өлшемшарттық әдіспен) |
|
|
№ 4 ТАПСЫРМА Проф. В.В. попофтың тәсілімен полигондағы координаттарды өсіру және бұрыштарды теңеу Қолданылған әдебиеттер
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I - ТАПСЫРМА
Орташа квадраттық қателіктерді анықтау, бірдей дәлдікті өлшемдер және өлшенген аргументтер функциялары
1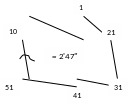 Есеп.
Тұйықталған полигонда бұрыштар n=10,
полигонның бұрыштық қиыспаушылық
=
2'47" (1.1
- сурет). Өлшенген бұрыштық mβ
орташа қателігін (ОКҚ) табу керек.
Есеп.
Тұйықталған полигонда бұрыштар n=10,
полигонның бұрыштық қиыспаушылық
=
2'47" (1.1
- сурет). Өлшенген бұрыштық mβ
орташа қателігін (ОКҚ) табу керек.
Берілгені:
n=15;
=3'15".
Табу керек: mβ = ?
Шешуі:
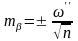 ;
1.1– Сурет
10 төбесі бар полигон үлгісі
;
1.1– Сурет
10 төбесі бар полигон үлгісі
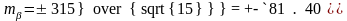 .
.
Жауабы: өлшенген бұрыштың орташа қателегі mβ = ± 81.40”
№ 1 есепті шығару үшін варианттар бойынша мәліметтер 1.1 – кестеде келтірілген.
1.1 - кесте №1 есептің варианттары бойынша мәліметтер
Вариант |
n |
|
Вариант |
N |
|
1 |
10 |
200 |
13 |
9 |
215 |
2 |
11 |
223 |
14 |
14 |
236 |
3 |
15 |
315 |
15 |
13 |
221 |
4 |
14 |
408 |
16 |
11 |
227 |
5 |
10 |
102 |
17 |
7 |
236 |
6 |
15 |
245 |
18 |
12 |
231 |
7 |
7 |
203 |
19 |
8 |
239 |
8 |
12 |
258 |
20 |
15 |
245 |
9 |
10 |
201 |
21 |
10 |
217 |
10 |
12 |
221 |
22 |
10 |
235 |
11 |
14 |
236 |
23 |
6 |
259 |
12 |
14 |
258 |
24 |
7 |
236 |
2 Есеп. Өлшенген горизонталь бұрыштың орташа квадраттық қателегі mβ = ± 31". n =12 төбеден тұратын полигонның бұрыштық қиыспаушылығын табу керек (1.2 сурет).
Б ерілгені:
ерілгені:
mβ = ± 17";
n =17
Табу керек: =?
Шешуі:
;  ;
1.2 –
Сурет
12 төбесі бар полигон үлгісі
;
1.2 –
Сурет
12 төбесі бар полигон үлгісі
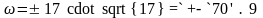
Жауабы: полигонның бұрыштық қиыспаушылығы ώ=70’9”
№ 2 есепті шығару үшін варианттар бойынша мәліметтер 1.2 – кестеде келтірілген.
1.2 – кесте №2 еспетің варианттары бойынша мәліметтер
Вариант |
n |
m |
Вариант |
N |
m |
1 |
20 |
11 |
13 |
10 |
15 |
2 |
21 |
12 |
14 |
12 |
12 |
3 |
17 |
17 |
15 |
16 |
11 |
4 |
7 |
10 |
16 |
11 |
18 |
5 |
14 |
16 |
17 |
7 |
22 |
6 |
11 |
15 |
18 |
14 |
19 |
7 |
6 |
24 |
19 |
8 |
18 |
8 |
9 |
25 |
20 |
12 |
29 |
9 |
15 |
31 |
21 |
17 |
28 |
10 |
10 |
20 |
22 |
18 |
30 |
11 |
13 |
20 |
23 |
16 |
25 |
12 |
6 |
22 |
24 |
17 |
21 |
3 Есеп. Ұшбұрышта екі А және В бұрыштары mA = ±21" және mВ = ±29" орташа квадраттық қателіктермен өлшенген (1.3 - сурет). С өлшенген бұрышының орташа квадраттық қателігін табу керек.

Берілгені:
mA = ±20" ;
mВ = ±14".
Табу керек: mC =?
1.3 – Сурет ұшбұрыш үлгісі
Шешуі:
С бұрышты тең болады: С= 180- (А + В),
онда ӨҚТ-ның негізгі формаласы бойынша:
m2C = (1 mA)2 + (1 mB)2 + …= (mA)2 + (mB)2 , онда
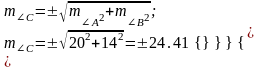
Жауабы: өлшенген бұрыштың орташа квадраттық қателегі mC = ±24.41”
№ 3 есепті шығару үшін варианттар бойынша мәліметтер 1.3 – кестеде келтірілген.
1.3 - кесте №3 есептің варианттары бойынша мәліметтер
Вариант |
mА |
mВ |
Вариант |
mА |
mВ |
1 |
11 |
11 |
13 |
28 |
23 |
2 |
12 |
15 |
14 |
28 |
21 |
3 |
20 |
14 |
15 |
29 |
21 |
4 |
15 |
18 |
16 |
20 |
21 |
5 |
17 |
27 |
17 |
19 |
32 |
6 |
20 |
25 |
18 |
21 |
28 |
7 |
28 |
15 |
19 |
31 |
25 |
8 |
15 |
28 |
20 |
21 |
15 |
9 |
19 |
21 |
21 |
25 |
23 |
10 |
11 |
22 |
22 |
26 |
15 |
11 |
17 |
15 |
23 |
14 |
19 |
12 |
17 |
28 |
24 |
12 |
15 |
4 Есеп. Бір бұрышта бірдей дәлдікпен төрт өлшенген. Өлшеулер нәтижелері 1.4 – кестесінде келтірілген.
1.4 – кесте Өлшеулер нәтижелері
-
өлшеулер
№
βi
1
37
13
14
2
37
13
27
3
37
13
20
4
37
13
17
Бұрышытың ықтимал мәні мен орташа квадраттық қателіктерін анықтау керек.
Берілгені:
β1= 371314; β3=371320;
β2=371327; β4=371317, n = 4.
Табу керек: m =?; m =? и m =?
Шешуі:
Өлшенген бұрыштың орташа мәні келесі формула бойынша есептейміз:
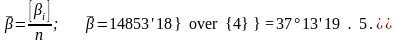
1.5- кесте Өлшенген бұрыштар қосындысын, ауытқуларды және ауытқулар квадратын есептеу
-
өлшеулер
№
βi
Vi
Vi Vi
()2
1
37
13
14
-0
00
5
25
2
37
13
27
-0
00
7
49
3
37
13
20
0
00
5
25
4
37
13
17
0
00
2
4
n = 4
[βi] =148º53’18”
[V]=0
[VV]=103
Өлшенген бұрыштыңорташа мәннен ауытқуын анықтаймыз, барлық есептеулер 1.5 – кестеде келтірілген:
 .
.
Ауытқулардың квадратын есептейміз, есептеулер 1.5 – кестеде келтіреміз: VV
Бір өлшенген бұрыштың орташа квадраттың ауытқуын анықтайды:

Орташа бұрыштың орташа квадраттық ауытқуын анықтайды:
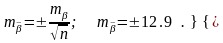
Жауабы: бір өлшенген бұрыштың о.к.қ. , m = 25.75”;
бұрыштың орташа мәнінің о.к.қ. , m =12.9”;
бұрыштың
ықтимал мәні,
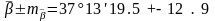 .
.
№ 4 есепті шығару үшін варианттар бойынша мәліметтер 1.6 – кестеде келтірілген
1.6 - кесте №4 есептің варианттары бойынша мәліметтер
Вариант |
n |
Вариант |
n |
Вариант |
n |
1 |
2 |
1 |
2 |
1 |
2 |
1 |
451522 451526 451528 451520 |
9 |
301213 301202 301209 301211 |
17 |
153013 153015 153018 153012 |
2 |
553505 553516 553518 553520 |
10 |
324215 324218 324223 324227 |
18 |
852015 852025 852018 852022 |
3 |
371314 371327 371320 371317 |
11 |
452111 452125 452118 452122 |
19 |
331116 331125 331118 331120 |
4 |
453015 453025 453018 453022 |
12 |
453027 453025 453032 453024 |
20 |
632320 632328 632315 632316 |
5 |
823210 823212 823218 823222 |
13 |
503213 503202 503209 503216 |
21 |
451725 451728 451718 451722 |
6 |
251113 251124 251110 251106 |
14 |
453015 453025 453018 453022 |
22 |
453015 453025 453018 453022 |
7 |
301213 301210 301201 301207 |
15 |
453215 453225 453218 453222 |
23 |
453415 453425 453418 453422 |
8 |
304215 304218 304223 304227 |
16 |
453115 453125 453118 453122 |
24 |
453515 453525 453518 453522 |
5 Есеп. Шақтаны бағдарлау кезінде жер асты түсірісінің бірінші тұрағының дирекциондық бұрыштары алынған, олар 1.7 – кестеде келтірілген. Дирекциондық бұрыштың ең ықтимал мәнін анықтау керек, оны анықтау дәлдігін бағалау жіне маркшейдерлік жұмыстар өндірісі бойынша техникалық нұсқаның рұқсатнамаларымен салыстыру керек. Рұқсатнама тең болады:
 , қайда
mпред=±03'.
, қайда
mпред=±03'.
1.7- кесте 1-2 (α1-2) бағытының дирекциондық бұрышы
-
өлшеулер
№
α1-2
1
207
53
54
2
207
53
32
3
207
54
27
4
207
54
13
5
207
55
07
Шешуі:
Өлшенген бұрыштың орташа мәні келесі формула бойынша есептеледі:
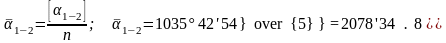
1.8- кесте Өлшенген дирекциондық бұрыштар қосындысын, ауытқулар мен ауытқулар квадраттын анықтау
-
өлшеулер
№
α1-2
Vi
VVi
()2
1
207
53
54
-0
00
19
361
2
207
53
32
-0
00
63
3969
3
207
54
27
0
00
13
169
4
207
54
13
0
00
15
225
5
207
55
07
0
00
16+
256
n = 5
[i]=1035º42'54"
[V]=0
Өлшенген бұрыштың орташа мәннен ауытқуын анықтаймыз, есептеулерді 1.8 – кестесінде келтіреміз.
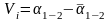 .
.
Ауытқу квадратын есептейміз есептеулерді 1.8 – кестесінде келтіреміз: VV.
Бір өлшенген бұрыштың орташа квадраттық ауытқуын есептейміз:
 .
.
Орташа бұрыштың орташа квадраттық ауытқуының қателегін есептейміз:
 .
.
6. Рұқсат
етілетін мәнді анықтаймыз:  .
.
Жауабы:
жұмыс
қажет етілетін дәлдікпен орындалды
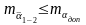 ,
дирекциондық бұрыштың ықтимал мәні
,
дирекциондық бұрыштың ықтимал мәні
 .
.
№ 5 есепті шығару үшін варианттар бойынша мәліметтер 1.9 – кестеде келтірілген.
1.9 - кесте №5 есептің варианттары бойынша мәліметтер
Вариант |
α1-2 |
Вариант |
α1-2 |
Вариант |
α1-2 |
1 |
1452532 1452602 1452455 1452540 1452615 |
9 |
1101530 1101559 1101639 1101652 1101743 |
17 |
1805510 1805534 1805649 1805632 1805710 |
2 |
1553345 1553356 1553508 1553438 1553457 |
10 |
1401530 1401559 1401651 1401643 1401736 |
18 |
1150533 1150551 1150635 1150642 1150740 |
3 |
2075354 2075332 2075427 2075413 2075507 |
11 |
1102535 1102549 1102635 1102641 1102757 |
19 |
1184538 1184547 1184626 1184646 1184727 |
4 |
2705137 2705228 2705130 2705159 2705203 |
12 |
1301531 1301556 1301625 1301647 1301751 |
20 |
1350530 1350559 1350639 1350652 1350743 |
5 |
925527 925535 925537 925433 925357 |
13 |
701543 701551 701635 701658 701745 |
21 |
1113534 1113551 1113633 1113648 1113727 |
6 |
952813 952824 952810 952806 952755 |
14 |
1104515 1104519 1104614 1104625 1104704 |
22 |
552430 552359 552439 552352 552343 |
7 |
1401530 1401559 1401636 1401646 1401751 |
15 |
1101530 1101559 1101637 1101632 1101727 |
23 |
1904130 1904059 1904139 1904052 1904303 |
8 |
1304245 1304318 1304223 1304307 1304237 |
16 |
1601515 1601539 1601649 1601632 1601753 |
24 |
602541 602557 602625 602620 602709 |
өлшеулер № |
Hi, М |
1 |
120.421 |
2 |
120.430 |
3 |
120.447 |
4 |
120.418 |
5 |
120.413 |
6 |
120.427 |
1.4 – Сурет – Шақта тереңдігін өлшеу үлгісі
|
|
1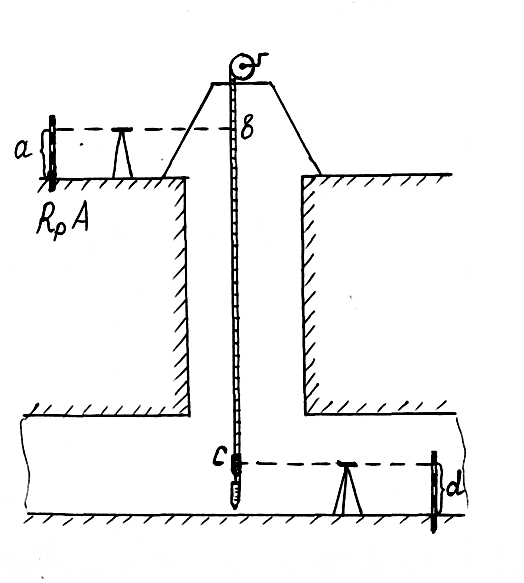 .20
– кесте Өлшеулер нәтижелері
.20
– кесте Өлшеулер нәтижелері
Шақта тереңдігінің мүмкін болатын тереңдігінің анықтау, маркшейдерлік жұмыстар өндірісі бойынша техникалық нұсқаудың рұқсатнамаларымен дәлдігін бағалау. Рұқсатнама тең болады:
 мұндағы
Δhрұқ=(10+0,2Н),
мм.
мұндағы
Δhрұқ=(10+0,2Н),
мм.
Шешуі:
Өлшенген ұзындықтардың орташа мәні келесі формуламен есептеледі:

1.21- кесте – Шақта тереңдігің өлшеудің қосындысын, ауытқулар мен ауытқу квадраттарын есептеу
өлшеулер № |
Hi, М |
V, мм |
VV, мм2 |
1 |
120.421 |
-5 |
22.5 |
2 |
120.430 |
5.5 |
30,25 |
3 |
120.447 |
-7,5 |
56,25 |
4 |
120.418 |
5,5 |
30,25 |
5 |
120.413 |
-2,5 |
6,25 |
6 |
120,427 |
1,5 |
2,25 |
n = 6 |
[Hi]= 722.556 |
[V]=0 |
[VV]=131,5 |
Өлшенген шақта тереңдегің орташа мәннен ауытқуын келесі формуламен есептеледі (1.21 кестеде қарандар)
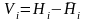 .
.
Ауытқулар квадратын есептйміз: VV (1.21 кестеде қарандар).
Бір өлшенген ұзындықтың орташа квадраттық ауытқуын анықтаймыз:

Орташа ұзындықтың орташа квадраттық ауытқуын анықтаймыз:
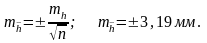
Техникалық нұсқау бойынша рұқсат етілетін мәнді есептейміз:
Δhрұқ=10+0,2*120.426=34,08мм,
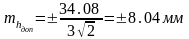 .
.
Жауабы:
жұмыс
қажет етілетін дәлдікпен орындалды
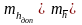 ,
шақта
тереңдігінің ықтимал мәні
,
шақта
тереңдігінің ықтимал мәні 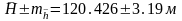 .
.
№ 6 есепті шығару үшін варианттар бойынша мәліметтер 1.22. – кестеде келтірілген.
1.22 – кесте №6 есептің варианттары бойынша мәліметтер
Вариант |
Нn |
Вариант |
Нn |
Вариант |
Нn |
1 |
2 |
1 |
2 |
1 |
2 |
1 |
100,321 100,343 100,330 100,340 100,337 100,325 |
9 |
140,125 140,145 140,131 140,140 140,139 140,129 |
17 |
120,222 120,231 120,228 120,225 120,227 120,230 |
2 |
110,128 110,149 110,134 110,142 110,136 110,128 |
10 |
130,525 130,545 130,531 130,540 130,539 130,529 |
18 |
90,155 90,145 90,151 90,140 90,139 90,149 |
3 |
120,421 120,430 120,447 120,418 120,413 120,427 |
11 |
100,421 100,417 100,428 100,426 100,419 100,422 |
19 |
150,625 150,645 150,631 150,640 150,639 150,629 |
1.22 – Кестенің жалғасы
1 |
2 |
1 |
2 |
1 |
2 |
4 |
200,351 200,372 200,336 200,357 200,370 200,354 |
12 |
100,715 100,725 100,730 100,729 100,732 100,722 |
20 |
100,421 100,417 100,428 100,426 100,419 100,422 |
5 |
137,210 137,215 137,212 137,222 137,217 137,208 |
13 |
210,521 210,532 210,529 210,527 210,534 210,518 |
21 |
195,345 195,355 195,350 195,352 195,339 195,346 |
6 |
150,511 150,525 150,536 150,520 150,518 150,527 |
14 |
100,821 100,817 100,828 100,826 100,819 100,822 |
22 |
100,121 100,117 100,128 100,126 100,119 100,122 |
7 |
140,320 140,332 140,325 140,336 140,328 140,330 |
15 |
170,351 170,357 170,358 170,356 170,359 170,352 |
23 |
250,425 250,413 250,424 250,422 250,418 250,420 |
8 |
110,421 110,417 110,419 110,424 110,428 110,420 |
16 |
260,945 260,935 260,940 260,942 260,938 260,925 |
24 |
180,267 180,257 180,261 180,260 180,249 180,255 |
7 Есеп. Жоғарғы деңгейжиектен төменгіге абсолюттік белгіні берудің дәлдігін анықтау (1.5 - сурет), егер келесілер берілген болса:
аспап биіктігі: mi= ±0,004м қателікпен i =1,20м;
белгі биіктігі: mv= ±0,001м қателікпен v =1,00м.
Көлбеу L ұзындықты және δ бұрышты өлшеу нәтижелері 1.23 – кестеде келтірілген.
1.23 – кесте – Өлшеулер нәтижелері
өлшеулер № |
Li М |
өлшеулер № |
δi |
|
||
|
|
|
||||
1 |
111,245 |
1 |
18 |
43 |
29 |
|
2 |
111.235 |
2 |
18 |
43 |
43 |
|
3 |
111.242 |
3 |
18 |
44 |
11 |
|
4 |
111.240 |
|
|
|||
5 |
111.238 |
|
|
|||
6 |
111.245 |
|
|
|||
|
||||||
Шешуі:
1. Өлшенген ұзындықтар мен көлбеу бұрыштардың орташа мәнін есептейді, ұзындықтардың және бұрыштардың қосындысын 1.24 және 1.25 –кестелерде анықтайды:

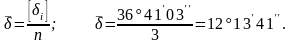
1.24 – кесте – Ұзындықтарды өндеу
№ |
Li ,м |
Vi , мм |
ViVi , мм2 |
1 |
111,245 |
0,8 |
0,64 |
2 |
111.235 |
-4,8 |
23,04 |
3 |
111.242 |
7,2 |
51,84 |
4 |
111.240 |
6,2 |
38,44 |
5 |
111.238 |
-10,8 |
116,64 |
6 |
111.245 |
1,2 |
1,44 |
n=6 |
[Li]=667.445 |
[Vi ]=0 |
[ViVi]=232,04 |
№ |
δi |
Vi, |
ViVi, ()2 |
1 |
12º13'19" |
-22 |
484 |
2 |
12º13'43" |
2 |
4 |
3 |
12º14'01" |
20 |
400 |
n=3 |
[δi ]= 36º41'03" |
[Vi ]=0 |
[ViVi]=888 |
2. Өлшенген ұзындықтың орташадан және өлшенген бұрыштың орташадан ауытқуларын анықтайды, барлық есептеулер 1.24 және 1.25кестелерде:
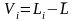 ;
; 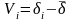 .
.
3. Ауытқулар квадраттары мен қосындыларын анықтаймыз: [ViVi].
Нәтижелер 1.24 және 1.25 кестелерде келтірілген.
4. Бір өлшенген ұзындықтың және бір өлшенген бұрыштың орташа квадраттық ауытқуын анықтайды:
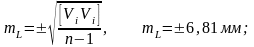
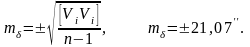
5. Орташа ұзындық пен орташа бұрыштың орташа квадраттық ауытқуларын анықтайды:

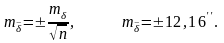
6. Өсімшелердің орташа мәнін анықтайды:
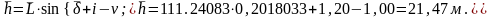
Өсімшененің о.к.қ. анықтайды:
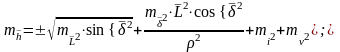

Жауабы:
өсімшенің ықтимал мәні:
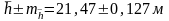 .
.
№ 7 есепті шығару үшін варианттар бойынша мәліметтер 1.26 – кестеде келтірілген.
1.26 – кесте - №7 есептің варианттары бойынша мәліметтер
№ варианта |
өлшеулер № |
Li, М |
м |
өлшеулер № |
δi |
||
|
|
|
|||||
1 |
2 |
3 |
4 |
5 |
6 |
||
1 |
1 |
100,424 |
i =1,20 |
1 |
11 |
23 |
29 |
2 |
100,419 |
v = 1,00 |
2 |
11 |
23 |
43 |
|
3 |
100,418 |
|
3 |
11 |
24 |
11 |
|
4 |
100,421 |
mi = 0,003 |
|
||||
5 |
100,420 |
mv= 0,012 |
|||||
6 |
100,417 |
|
|||||
2 |
1 |
120,325 |
i =1,20 |
1 |
10 |
23 |
05 |
2 |
120,314 |
v = 1,00 |
2 |
10 |
23 |
35 |
|
3 |
120,318 |
|
3 |
10 |
24 |
06 |
|
4 |
120,326 |
mi = 0,004 |
|
||||
5 |
120,320 |
mv= 0,014 |
|||||
6 |
120,317 |
|
|||||
3 |
1 |
111,245 |
i =1,20 |
1 |
18 |
43 |
29 |
2 |
111,235 |
v = 1,00 |
2 |
18 |
43 |
43 |
|
3 |
111,242 |
|
3 |
18 |
44 |
11 |
|
4 |
111,240 |
mi = 0,007 |
|
||||
5 |
111,238 |
mv= 0,021 |
|||||
6 |
111,245 |
|
|||||
4 |
1 |
95,613 |
i =1,20 |
1 |
11 |
47 |
57 |
2 |
95,627 |
v = 1,00 |
2 |
11 |
48 |
00 |
|
3 |
95,630 |
|
3 |
11 |
49 |
25 |
|
4 |
95,617 |
mi = 0,008 |
|
||||
5 |
95,623 |
mv= 0,023 |
|||||
6 |
95,629 |
|
|||||
5 |
1 |
47,617 |
i =1,20 |
1 |
17 |
18 |
17 |
2 |
47,605 |
v = 1,00 |
2 |
17 |
17 |
54 |
|
3 |
47,651 |
|
3 |
17 |
18 |
05 |
|
4 |
47,619 |
mi = 0,007 |
|
||||
5 |
47,627 |
mv= 0,014 |
|||||
6 |
47,603 |
|
|||||
6 |
1 |
94,434 |
i =1,20 |
1 |
11 |
14 |
00 |
2 |
94,447 |
v = 1,00 |
2 |
11 |
14 |
31 |
|
3 |
94,452 |
|
3 |
11 |
15 |
28 |
|
4 |
94,437 |
mi = 0,010 |
|
||||
5 |
94,451 |
mv= 0,025 |
|||||
6 |
94,441 |
|
|||||
7 |
1 |
92,757 |
i =1,20 |
1 |
11 |
17 |
00 |
2 |
92,775 |
v = 1,00 |
2 |
11 |
16 |
07 |
|
3 |
92,759 |
|
3 |
11 |
18 |
31 |
|
4 |
92,761 |
mi = 0,013 |
|
||||
5 |
92,765 |
mv= 0,018 |
|||||
6 |
92,771 |
|
|||||
8 |
1 |
94,647 |
i =1,20 |
1 |
11 |
25 |
04 |
2 |
94,657 |
v = 1,00 |
2 |
11 |
25 |
57 |
|
3 |
94,665 |
|
3 |
11 |
26 |
31 |
|
4 |
94,651 |
mi = 0,021 |
|
||||
5 |
94,659 |
mv= 0,011 |
|||||
6 |
94,663 |
|
|||||
1.26 – Кестенің жалғасы
1 |
2 |
3 |
4 |
5 |
6 |
||
9 |
1 |
90,317 |
i =1,20 |
1 |
14 |
11 |
03 |
2 |
90,327 |
v = 1,00 |
2 |
14 |
12 |
00 |
|
3 |
90,335 |
|
3 |
14 |
12 |
31 |
|
4 |
90,321 |
mi = 0,019 |
|
||||
5 |
90,331 |
mv= 0,014 |
|||||
6 |
90,334 |
|
|||||
10 |
1 |
50,245 |
i =1,20 |
1 |
11 |
20 |
37 |
2 |
50,235 |
v = 1,00 |
2 |
11 |
19 |
48 |
|
3 |
50,242 |
|
3 |
11 |
21 |
20 |
|
4 |
50,240 |
mi = 0,010 |
|
||||
5 |
50,238 |
mv= 0,012 |
|||||
6 |
50,245 |
|
|||||
11 |
1 |
195,613 |
i =1,20 |
1 |
15 |
16 |
01 |
2 |
195,627 |
v = 1,00 |
2 |
15 |
15 |
43 |
|
3 |
195,630 |
|
3 |
15 |
17 |
30 |
|
4 |
195,617 |
mi = 0,027 |
|
||||
5 |
195,623 |
mv= 0,013 |
|||||
6 |
195,629 |
|
|||||
12 |
1 |
95,137 |
i =1,20 |
1 |
11 |
45 |
19 |
2 |
95,141 |
v = 1,00 |
2 |
11 |
46 |
23 |
|
3 |
95,156 |
|
3 |
11 |
45 |
31 |
|
4 |
95,139 |
mi = 0,021 |
|
||||
5 |
95,143 |
mv= 0,022 |
|||||
6 |
95,151 |
|
|||||
13 |
1 |
120,613 |
i =1,20 |
1 |
13 |
47 |
57 |
2 |
120,627 |
v = 1,00 |
2 |
13 |
48 |
00 |
|
3 |
120,630 |
|
3 |
13 |
49 |
25 |
|
4 |
120,617 |
mi = 0,008 |
|
||||
5 |
120,623 |
mv= 0,023 |
|||||
6 |
120,629 |
|
|||||
14 |
1 |
64,175 |
i =1,20 |
1 |
11 |
34 |
23 |
2 |
64,184 |
v = 1,00 |
2 |
11 |
34 |
59 |
|
3 |
64,193 |
|
3 |
11 |
35 |
51 |
|
4 |
64,179 |
mi = 0,031 |
|
||||
5 |
64,187 |
mv= 0,027 |
|||||
6 |
64,190 |
|
|||||
15 |
1 |
94,657 |
i =1,20 |
1 |
11 |
13 |
29 |
2 |
94,667 |
v = 1,00 |
2 |
11 |
13 |
43 |
|
3 |
94,675 |
|
3 |
11 |
14 |
11 |
|
4 |
94,661 |
mi = 0,013 |
|
||||
5 |
94,669 |
mv= 0,012 |
|||||
6 |
94,673 |
|
|||||
8 Есеп. АВС үшбұрышында: АВ = с, жағы, А және С сәйкес mс , mА және mС, қателіктерімен бұрыштары өлшенген, мәліметтер 1.27 – кестеде клтірілген.
1.27 - кесте Берілген мәліметтер
Берілген мәліметтер |
Табу керек |
|||||||||||
с, м |
mc, м |
А бұрышы |
mА, сек. |
С бұрышы |
mС, сек. |
а, м |
mа, м |
|||||
|
|
|
|
|
|
|||||||
357.450 |
0.090 |
57 |
41 |
22 |
18 |
64 |
08 |
42 |
18 |
? |
? |
|
СВ = а жағы мен жақты анықтау mа қателігін табу керек .
Шешуі:
1. СВ = а жағын синустар теоремасы бойынша анықтайды:
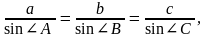 бұдан
бұдан
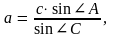
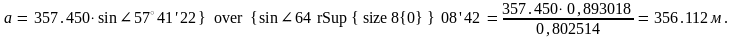
2. а, жағының қателігін қателіктер теориясының негізгі формуласы бойынша табылады:

мұнда 
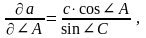
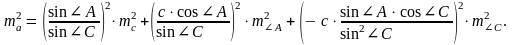
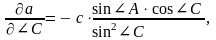 сонда
сонда

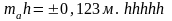
Жауабы:
СВ
жағының ықтимал мәні:
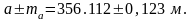
№ 8 есепті шығару үшін варианттар бойынша мәліметтер 1.28 – кестеде келтірілген.
1.28 - кесте №8 есептің варианттары бойынша мәліметтер
-
Берілген мәліметтер
вариант№
с,
м
mc,
м
А бұрышы
mА,
сек.
С бұрышы
mС,
сек.
1
2
3
4
5
6
7
1
450,380
0,460
60
18
00
84
32
08
00
48
2
502,280
0,350
50
20
00
68
48
07
00
60
3
357,450
0,090
57
41
22
18
64
08
42
18
4
552,170
0,590
68
25
00
60
24
51
00
90
5
201,810
0,080
47
18
30
10
62
18
30
15
6
345,270
0,260
50
15
00
84
43
35
00
58
7
309,180
0,070
54
11
00
15
43
01
50
15
8
251,360
0,220
42
22
00
66
48
13
00
84
9
446,640
0,350
54
35
00
36
36
35
00
72
10
276,460
0,370
56
23
00
71
38
46
00
63
11
199,770
0,040
57
33
00
20
57
00
48
20
12
457,660
0,100
60
19
40
10
54
19
30
10
13
350,200
0,310
50
46
00
48
40
18
00
72
14
206,930
0,150
38
30
00
90
52
34
00
60
15
295,470
0,360
58
16
00
77
33
49
00
63
16
344,670
0,080
41
10
18
08
48
59
00
08
17
342,160
0,200
35
16
15
17
67
17
45
15
18
154,220
0,120
34
36
00
72
56
05
00
90
19
289,100
0,070
61
51
18
15
48
43
10
15
20
183,150
0,050
43
18
10
20
50
10
22
20
21
440,880
0,440
48
37
00
81
39
37
00
66
22
241,360
0,070
54
11
00
15
43
01
50
15
23
250,450
0,220
42
22
00
66
48
13
00
84
24
230,440
0,350
54
35
00
36
36
35
00
72
25
264,150
0,110
63
15
18
14
53
22
15
14
№ II ТАПСЫРМА

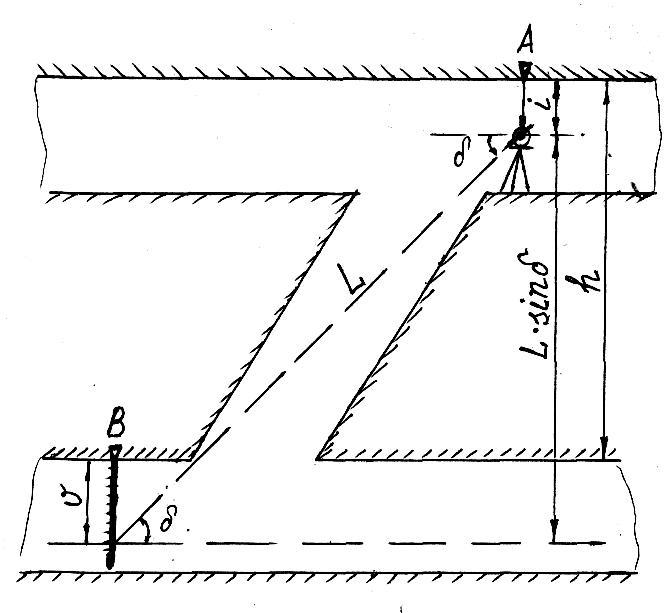 1.5
-
сурет
Жоғарғы
деңгейжиектен төменгіге абсолюттік
белігін беру үлгісі
1.5
-
сурет
Жоғарғы
деңгейжиектен төменгіге абсолюттік
белігін беру үлгісі