
Тестовые задания по математике 2011
Разработала ст. преп кафедры ЕНД Чиналиева М.Т..
( 1 курс технолог. университет )
1.
Вычислите
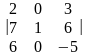 .
.
* A) -28;
B) -8;
C) -16;
D) -1;
E) 8.
2. Вычислите : .
3;
0 ;
–32;
8; *
12.
3.
Решить систему уравнении:
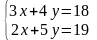 .
.
(2,4);
(1,3);
(2,3); *
(-1,4);
(-2,-3).
4.
Найти AB матриц , если
A =
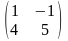 и B =
и B =

 .
.
* A)
 ; B)
; B)
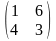 ;
;
C)
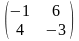 ;
;
D)
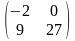 ; E)
; E)

5.
Найти длину
вектора
 ,
если M(4;
-2 )
и N(1;
2 ).
,
если M(4;
-2 )
и N(1;
2 ).
7;
6;
5; *
2;
3.
6.
Даны точки А( 5; 3; 1) и В( 4; 5; -1) . Найти
длину вектора
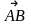
A) 2;
B) 5;
C) 4;
* D) 3;
E) 8.
7.
Найти интеграл

A) ln (3x + 1 ) + C;
B) 3ln ( 3x + 1 ) + C;
C)
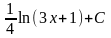 ;
;
* D)
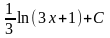 ;
;
E) 6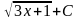 .
.
8. Найти интеграл .
A)
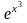 +C;
+C;
* B)
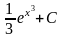 ;
;
C) 3 +C;
D)
+ + C;
+ C;
3 + x 3 + C .
9. Чему равен интеграл
![]() ?
?
A)
![]() ;
;
B) 0;
* C)
![]() ;
;
D)
![]() ;
;
E)
![]() .
.
10.
Вычислите интеграл
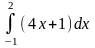
A) 17;
* B) 9;
C) 4;
D) 6;
E) 16.
11. Вычислите интеграл .
* A) 1 ;
B) 3;
C) e;
D) 3e ;
E)
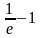 .
.
12.
Вычислить интеграл
 .
.
A) 1 ;
B) 3;
C) e;
D) 3e ;
* E)
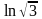 .
.
13. Правило Лопиталя:
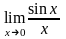 =
1;
=
1; =
=
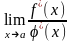 ;
*
;
*(
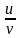 )/
=
)/
=
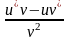 ;
;( x – x0)2 = 2py;
 .
.
14.
Вычислить интегралы
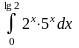 .
.
A) ln10;
* B)
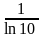 ;
;
C)
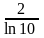 ;
;
2;
100.
15.
В равенстве
 выражение F(x)+C
называется
выражение F(x)+C
называется
первообразной; *
четная функция;
нечетная функция;
сложная функция;
степенная функция.
16. Точки, в которых вторая производная функции равна нулю или не существует,
называются
* A) критическими точками 2 – го рода;
B) точками разрыва;
C) критическими точками 1 – го рода;
D) дифференцируемой точкой;
E) точками перегиба.
17.
Даны векторы
 (
3; -1; 4) и
(
3; -1; 4) и
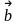 ( 0; 2;1) . Найти вектор
( 0; 2;1) . Найти вектор
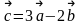 .
.
* A)
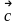 (
9; -7; 10 );
(
9; -7; 10 );
B) ( 0; -2; 5 );
C) ( 1; -5; 12 );
D) ( 1; 4; 0 );
E) ( 9; 1; -4).
18. Второй замечательный предел.
A) = 1;
= ;
( )/ = ;
( x – x0)2 = 2py;
. *
19. Первый замечательный предел.
= 1; *
= ;
( )/ = ;
( x – x0)2 = 2py;
20. Вычислите f(-1 ), если f(x) = x3 - 4x2 +15
* A) 10
B) 12
C) 18
D) 14
E) 11
21.
Найти предел
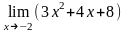
A) 20
* B) 12
C) 30
D) -4
E) -2
22.
Вычислить
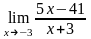
A) -19
B) 0
* C) ∞
D) -56
E) -
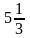
23. Дана функция f(x) = x2 – 3x . Найти f/ (-3)
A) -3
B) 2
* C) -9
D) -2
E) 1
24. Вычислите f /(-2 ), если f(x) = x3 - 2x2 + 3х -5
A) 3
* B) 23
C) 18
D) 8
E) -17
25. Дана функция f (x ) = 31-x . Найти f ( -1) .
* A) 9
B) 0
C) 3
D)

E) 1
26.
Найти интеграл
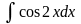
A)
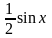
B) 2 sin x
C) + C
* D)
 +
С
+
С
E) sin x + C
27.
Найти область определения функции
y =
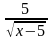
A) ( ∞; 5 )
B) ( 0; ∞ )
C) ( - ∞; + ∞ )
D) ( 0; 5 )
* E) ( 5; ∞ )
28.
Вычислите

* A) 6,4
B) 32
C) -1,4
D) -2,5
E) 1,5
29. Дана функция f( x) = sinx2 . Найти f / ( x ).
A) cos x2
B) 2cos x
C) 2 sin x
D) cos2x
* E) 2x cosx2
30.
Найти интеграл

A) х2 +3 +С
B) 2 х2 + 3х +С
* C) х2 + 3х + С
D) 2х + 3
E) 5х + С
31. Метод подстановки в неопределенном интеграле.
* A)
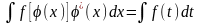
B)
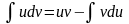
C)
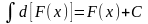
D)

E)

32.
Вычислите
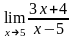
A) 19
B) 0
* C)
D) 1
E) 0,8
33.
Вычислите предел
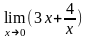
A) 1
* B) ∞
C) 4
D) -2
E) 0
34.
Вычислите f ( -3 ), если
f(x) = x2
+ 3x -

* A) 9
B) 3
C) -9
D) -3
E) 0
35.
Найти предел
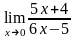
A) 1,5
* B) -0,8
C) -1
D) -2
E) 0,8
36.
Решить систему уравнений
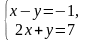
A) (1; -3 )
B) ( 2; -4)
C) (3; 3 )
* D) ( 2; 3 )
E) (5; 0 )
37. Найти производную функции y = 5lnx – x2
* A)
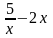
B)
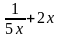
C) -
D) -
38. Дана функция f(x) = log3 (2 – x) . Найти f / (-1 )
A) ln3
B) 3ln3
* C) -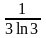
D)
E)
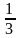
39.
Найти предел
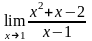
A) 2
B) 0
C) 1
D) -3
* E) 3
