Билет 1.

3 Вопрос. Касательная к окружности:

А) Прямая называется касательной к окружности, если она имеет только одну общую точку с этой окружностью.

Б) Касательная к окружности перпендикулярна радиусу, проведенному к точке касания. Если прямая проходит через точку радиуса, лежащую на окружности, и прямая перпендикулярна этому радиусу, то прямая является касательной к данной окружности.

В) Отрезки касательных, проведенных из одной точки, равны.

Г) Если из точки, лежащей вне окружности, проведены две секущие, то произведение одной секущей на её внешнюю часть равно произведению другой секущей на её внешнюю часть. Если из одной точки проведены к окружности касательная и секущая, то произведение всей секущей на её внешнюю часть равно квадрату касательной. AD^2 = AB* AC.

Билет 2.

3 вопрос. Свойства прямоугольного треугольника:

А) 1. Высота, проведенная к гипотенузе, есть среднее пропорциональное между проекциями катетов на гипотенузу.

2. Катет есть среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу.

Б) Медиана в прямоугольном треугольнике — это отрезок, который соединяет вершину треугольника и середину противоположной стороны, то есть вершину острого угла с серединой противолежащего катета или вершину прямого угла с серединой гипотенузы. 1) Медиана, проведенная к гипотенузе, равна половине гипотенузы. 2) Медиана, проведенная к гипотенузе, равна радиусу описанной около прямоугольного треугольника окружности.

В) Центр вписанной в треугольник окружности находится в точке пересечения его биссектрис. Если все вершины многоугольника лежат на окружности, то окружность называется описанной около треугольника, а треугольник - вписанным в эту окружность. Около любого треугольника можно описать окружность и при этом только одну. Центр описанной около треугольника окружности находится в точке пересечения серединных перпендикуляров. Радиус описанной около равностороннего треугольника окружности определяется по формуле:

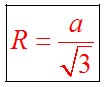
Радиус вписанной в равносторонний треугольник окружности определяется по формуле:

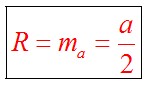
Радиус вписанной в прямоугольный треугольник окружности определяется по формуле:

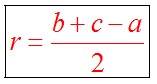
Билет 3.

Вопрос 3

А) Первый признак подобия треугольников

Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.

Второй признак подобия треугольников

Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.

Третий признак подобия треугольников

Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.

Б) 3) признак- если у одного треуг. 3 стороны равны 3-м сотронам другого треугольника то такие треугольники равны. 1) признак- если у одного треуг. 2 стороны и угол между ними равны 2-м сторонам и углу между ними другого треуга. то такие трег. Равны. 2)если у одного треугольника 2 угла и сторона между ними равны 2-м углам и стороне между ними другого треуга то такие треугольники равны.

В) Формула площади треугольника по стороне и высоте

Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты.

Формула площади треугольника по трем сторонам

Формула Герона

S = √p(p - a)(p - b)(p - c)

Формула площади треугольника по двум сторонам и углу между ними

Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними.

Формула площади треугольника по трем сторонам и радиусу описанной окружности

S = a · b · с :4R

Формула площади треугольника по трем сторонам и радиусу вписанной окружности

Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.

S = p · r

Г) Отношение площадей подобных треугольников равно квадрату коэффициента подобия, следовательно коэффициент подобия =3. Отношение периметров подобных треугольников равно коэффициенту подобия, следовательно в этой задаче отношение периметров =3.