Одноканальная смо с отказами

Пусть λ — интенсивность поступления заявок в систему (среднее число заявок, поступающих в систему за единицу времени).

 – интенсивность обслуживания,

t_об – среднее время обслуживания одного клиента.      Относительная пропускная способность:

Эта величина равна вероятности Р₀ того, что канал обслуживания свободен.       Абсолютная пропускная способность (А) — среднее число заявок, которое может обслужить система массового обслуживания в единицу времени:

     Вероятность отказа в обслуживании заявки «канал обслуживания занят»:

         Р_отк средняя доля необслуженных заявок среди поданных.

Задана 4.1.: Имеется одноканальная СМО с отказами.. Интенсивность потока заявок λ= 1. Средняя продолжительность обслуживания — t_об=1,8 часа.     Определить:      относительную пропускной способности q;      абсолютную пропускной способности А;      вероятности отказа Р_отк;      Сравнить фактическую пропускную способность СМО с номинальной, которая была бы, если бы каждая заявка обслуживалась точно 1,8 часа и заявки следовали один за другим без перерыва.      Решение (подготовить таблицу в Excel)

Одноканальная СМО с ожиданием и ограниченной очередью

     СМО имеет один канал.

Входящий поток имеет интенсивность λ.

Интенсивность потока обслуживания равна μ (т. е. в среднем непрерывно занятый канал будет выдавать μ обслуженных заявок).

Заявка, поступившая в момент, когда канал занят, становится в очередь и ожидает обслуживания.

P_n  - вероятность того, что в системе находится n заявок.

ρ=λ/μ  - приведенная интенсивность потока. 

Вероятность того, что канал обслуживания свободен и в системе нет ни одного клиента, равна:

С учетом этого можно обозначить

Определим характеристики одноканальной СМО с ожиданием и ограниченной длиной очереди, равной (N-1):      вероятность отказа в обслуживании заявки:

     относительная пропускная способность системы:

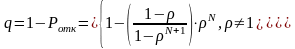
     абсолютная пропускная способность:      А=q∙λ;      среднее число находящихся в системе заявок:

     среднее время пребывания заявки в системе:

     средняя продолжительность пребывания клиента (заявки) в очереди:      W_q=W_s- 1/μ;      среднее число заявок (клиентов) в очереди (длина очереди):      L_q=λ(1-P_N)W_q.

Задана 4.2.: Дана одноканальная СМО.

Ограничение на очередь - 3 места ( т.е. N— 1=3 и если в этом случае появляется четвертая заявка, то она уходит из очереди).

Поток заявок имеет интенсивность λ=0,85 (заявок в час).

Время обслуживания заявки в среднем равно t_об =1,05 час.      Требуется определить вероятностные характеристики СМО, работающего в стационарном режиме. Решение μ=1/ t_об=1/1,05=0,952

ρ=λ/μ=0,85/0,952=0,893 =0,248 P₁=r∙P₀=0,893∙0,248=0,221; P₂=r²∙P₀=0,893²∙0,248=0,198; P₃=r³∙P₀=0,893³∙0,248=0,177; P₄=r⁴∙P₀=0,893⁴∙0,248=0,158.

P_отк=Р₄=r⁴∙P₀≈0,158.

q=1–P_отк=1-0,158=0,842.

А=λ∙q=0,85∙0,842=0,716 (заявок в час).      Среднее число заявок, находящихся на обслуживании и в очереди :

     Среднее время пребывания заявки в системе:

часа.      Средняя продолжительность пребывания заявки в очереди на обслуживание:      W_q=W_s-1/μ=2,473-1/0,952=1,423 часа.      Среднее число заявок в очереди (длина очереди):      L_q=λ∙(1-P_N)∙W_q=0,85∙(1-0,158)∙1,423=1,02.      Работу СМО можно считать удовлетворительной, так как СМО не обнаруживает автомобили в среднем в 15,8% случаев (Р_отк=0,158).