Задача безусловной оптимизации для функции одной переменной

Если существует производная f '(a), то функция f(x) может иметь в точке a внутренний максимум или минимум лишь в том случае, когда

f '(a)=0

(необходимое условие экстремума).

Если существует вторая производная f ''(a), то функция f(x) имеет в точке а

максимум при f '(a)=0 и f ''(a)<0,

минимум при f '(a)=0 и f ''(a)>0.

Условия являются достаточными условиями экстремума.

Функции нескольких переменных

Необходимые условия оптимальности следующие: если функция f (x₁, x₂, …, x_n) дифференцируема в точке а=(а₁, а₂, …, а_n), то она может иметь в этой точке внутренний максимум или минимум лишь в том случае, когда ее первый дифференциал df обращается в этой точке в нуль, т.е. когда

Достаточные условия оптимальности: если функция f имеет в точке а непрерывные вторые частные производные и если в этой точке выполняются необходимые условия, то в случае, когда второй дифференциал

есть отрицательно определенная квадратичная форма, функция f имеет в точке а максимум, если d ² f есть положительно определенная квадратичная форма, то функция f имеет в точке а минимум. Если квадратичная форма не определена, экстремума в точке а нет.

Задача 2.1. Среди всех прямоугольников с периметром фиксированной длины L необходимо найти прямоугольник максимальной площади. Какую длину и ширину будет иметь такой прямоугольник?

Задача 2.2. Исследовать на экстремум функцию двух переменных

Задача 2.3. Исследовать на экстремум функцию двух переменных

Задача 2.4. Даны зависимости спроса D=400-20p, и предложения S=70+10p.

Найдите равновесную цену и выручку при равновесной цене. Найдите цену, при которой выручка будем максимальной и саму эту максимальную выручку

Функция выручки (T) = Функция спроса (D)*цену (P)

Задача 2.5. Для одного из предприятий-монополистов зависимость объема спроса на продукцию q (единиц в месяц) от ее цены p (тыс. руб.) задается формулой: q = 150 − 10p. Определите максимальный уровень цены p (в тыс. руб.), при котором значение выручки предприятия за месяц r = q · p составит не менее 440 тыс. руб.

Задача 2.6. В фермерском хозяйстве решили продавать молоко по 38 руб. за литр и куриные яйца по цене 20 руб.за десяток. Издержки при производстве можно описать формулой

Найти максимальную выручку и количество производимой продукции

Задача 2.7. Определить оптимальное для производителя значение выпуска x, при условии, что весь товар реализуется по фиксированной цене за единицу p=14 , если известен вид функции издержек C(x) = 13+2x+x³.

Задача 2.8. Найти максимальную прибыль, которую может получить фирма производитель, при условии, что весь товар реализуется по фиксированной цене за единицу р=10,5 и функция издержек имеет вид C(x)=10+x/2+x²/4 .

Контрольная работа к лекции 2

1. Определить оптимальное для производителя значение выпуска x₀, при условии, что весь товар реализуется по фиксированной цене за единицу p=8 и известен вид функции издержек .

2. Найти максимальную прибыль, которую может получить фирма-производитель, при условии, что весь товар реализуется по фиксированной цене за единицу p =40 и известен вид функции издержек

3. При производстве монополией x единиц товара за единицу . Определить оптимальное для монополии значение выпуска x₀ (предполагается что весь произведённый товар реализуется), если издержки имеют вид .

4. Функция издержек имеет вид . Доход от реализации единицы продукции равен 50. Найти максимальное значение прибыли, которое может получить производитель.

5. На начальном этапе производства фирма минимизирует средние издержки, причём функция издержек имеет вид 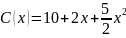.  В дальнейшем цена на единицу товара устанавливается равной р=37. На сколько единиц товара фирме следует увеличить выпуск?

На сколько при этом изменятся средние издержки?

6. Даны зависимости спроса D(p) и предложения S(p) от цены.

Найдите: 1) равновесную цену и выручку при равновесной цене;

                 2) цену, при которой выручка максимальна и саму эту 

                     максимальную выручку.

Построить график зависимостей. (можно выбрать любой номер задания)

№ варианта
1	D=1000-10p S=100+10p	5	D=600-8p S=120+8p
2	D=800-10p S=200+10p	6	D=400-5p S=100+5p
3	D=1000-20p S=70+10p	7	D=500-5p S=50+5p
4	D=400-20p S=70+10p	8	D=200-10p S=35+5p
10	D=300-4p S=60+4p	9	D=500-10p S=50+5p

Лекция 3. Модель межотраслевого баланса

Балансовые модели предназначены для анализа и планирования производства и распределения продукции на различных уровнях — от отдельного предприятия до народного хозяйства в целом.

Цель балансового анализа — ответить на вопрос, возникающий в макроэкономике и связанный с эффективностью ведения многоотраслевого хозяйства: каким должен быть объем производства каждой из п отраслей, чтобы удовлетворить все потребности в продукции этой отрасли?

При этом каждая отрасль выступает, с одной стороны, как производитель некоторой продукции; а с другой — как потребитель продукции и своей, и произведенной другими отраслями. Предположим, что рассматривается п отраслей промышленности, каждая из которых производит свою продукцию.

Пусть общий объем произведенной продукции i -й отрасли равен x_i.

Тогда объем продукции произведенный всеми отраслями называется вектором валового продукта.

Рассмотрим, на что тратится продукция, производимая отраслью.

Часть продукции идет на внутрипроизводственное потребление данной отраслью и потребление другими отраслями, связанными с этой отраслью.

Количество продукции i-й отрасли, предназначенной для потребления j-й отраслью обозначим x_ij .

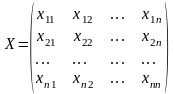
Оставшаяся часть предназначена для реализации потребителям вне производственной сферы. Эта часть называется конечным продуктом.

Пусть i-ая отрасль производит y_i  конечного продукта. Тогда

называется вектором конечного продукта. 

Этот объем составляет обычно более 75% всей произведенной продукции. В него входят создаваемые в хозяйстве запасы, личное потребление граждан, обеспечение общественных потребностей (просвещение, наука, здравоохранение, развитие инфраструктуры и т.д.), поставки на экспорт.

Рассмотрим процесс производства за некоторый период времени (например, год). Так, как валовой объем продукции любой i-й отрасли равен суммарному объему продукции, потребляемой n отраслями, и конечного продукта, то уравнение баланса между производством и потреблением будет иметь вид:

(i=1,2,…n) (1)      Уравнения (1) называются соотношениями баланса.      Одной из задач балансового анализа является определение валового продукта Y_i, если известно распределение конечного X_i .

Для этого введем коэффициенты прямых затрат:

     Они получаются в результате деления всех элементов каждого столбца матрицы x_ij на соответствующий элемент матрицы межотраслевых производственных связей Х.

Коэффициенты прямых затрат имеют смысл количества потребления продукции j-й отрасли, необходимой для производства единицы продукции i-й отраслью. Они остаются постоянными в течение ряда лет. Это обусловливается примерным постоянством используемой технологии.

Материальные издержки пропорциональны объему производимой продукции. Принцип линейности распространяют и на другие виды издержек (например, на оплату труда), а также на нормативную прибыль.

Итак, согласно гипотезе линейности имеем

Очевидно

Подставив последнее выражение в соотношение баланса (1), получим:

Если обозначить матрицу коэффициентов прямых затрат как

и тогда соотношение баланса в можно записать в виде:

X=AX+Y

    Из последнего выражения можно найти значение конечного продукта при известном значении валового:

Y=X-AX=(E-A)X, где

единичная матрица, того же размера, что и А.

Матрицу S = (E – A)^-1 называют матрицей полных затрат.

Основная задача межотраслевого баланса состоит в отыскании такого вектора валового выпуска X, который при известной матрице прямых затрат А обеспечивает заданный вектор конечного продукта Y.

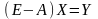
Модель Леонтьева называется продуктивной, если система X = (E – A)^-1×Y

имеет неотрицательное решение

Имеется несколько критериев продуктивности матрицы А.

Один из них: матрица А продуктивна, если максимум сумм элементов ее столбцов не превосходит единицы, причем хотя бы для одного из столбцов сумма элементов строго меньше единицы

причем существует номер j такой, что

Пример выполнения контрольного задания.

В некотором регионе имеются две основные отрасли народного хозяйства: машиностроение (м/с) и сельское хозяйство (с/х). Баланс этих отраслей за отчетный период определяется таблицей

 

Контрольная работа к лекции 3

1. Имеется баланс двух взаимосвязанных отраслей (машиностроение и сельское хозяйство):

Производство	Потребление с/х м/с	Валовой продукт
с/х м/с	15 5 5 10	76 55

     Найти конечный продукт каждой отрасли, матрицу коэффициентов прямых затрат. Какой будет валовой продукт каждой отрасли, если конечный продукт сельского хозяйства необходимо увеличить на 20 %, а машиностроения уменьшить на 10 %.     

2. Имеется баланс двух взаимосвязанных отраслей (машиностроение и сельское хозяйство):

Производство	Потребление с/х м/с	Валовой продукт
с/х м/с	5 5 7 4	78 67

     Найти конечный продукт каждой отрасли, матрицу коэффициентов прямых затрат. Какой будет валовой продукт каждой отрасли, если конечный продукт сельского хозяйства необходимо увеличить на 50 %, а машиностроения уменьшить на 50 %.  

3. Имеется баланс двух взаимосвязанных отраслей (машиностроение и сельское хозяйство):

Производство	Потребление с/х м/с	Валовой продукт
с/х м/с	15 5 5 10	75 60

     Найти валовый продукт каждой отрасли, матрицу коэффициентов прямых затрат. Какой будет валовой продукт каждой отрасли, если конечный продукт сельского хозяйства необходимо увеличить на 20 %, а машиностроения уменьшить на 10 %.     

4. Межотраслевой баланс производства и распределения продукции для 4 отраслей имеет вид     

Производящие отрасли	Потребляющие отрасли 1 2 3 4	Валовой продукт
1 2 3 4	60 60 85 5 50 20 85 15 45 30 75 10 90 10 40 5	800 400 800 250

     Найти конечный продукт каждой отрасли, матрицу коэффициентов прямых затрат. Какой будет конечный продукт каждой отрасли, если валовой продукт первой отрасли увеличится в 2 раза, у второй увеличится на половину, у третьей не изменится, у четвертой – уменьшится на 10 процентов.     

5. Межотраслевой баланс производства и распределения продукции для 4 отраслей имеет вид

Производящие отрасли	Потребляющие отрасли 1 2 3 4	Конечный продукт
1 2 3 4	30 25 50 70 90 80 75 80 85 10 85 60 60 40 40 20	475 195 420 370

     Найти валовый продукт каждой отрасли, чистую продукцию каждой отрасли, матрицу коэффициентов прямых затрат. Какой будет конечный продукт каждой отрасли, если валовой продукт первой отрасли увеличится в 2 раза, у второй увеличится на половину, у третьей не изменится, у четвертой – уменьшится на 10 процентов.    

6. Имеется баланс трех взаимосвязанных отраслей за предыдущий период:

Производство	Потребление Отрасль 1 Отрасль 2 Отрасль 3	Конечный продукт
Отрасль 1 Отрасль 2 Отрасль 3	2 10 4 4 10 6 4 2 4	20 24 28

     Найти валовой продукт каждой отрасли, чистую продукцию каждой отрасли, матрицу коэффициентов прямых затрат. Какой будет валовой продукт каждой отрасли, если конечный продукт первой отрасли необходимо увеличить на 50 %, второй уменьшить на 4 единицы, а третьей увеличить на 6 единиц.   

7. Имеется баланс трех взаимосвязанных отраслей за предыдущий период:

Производство	Потребление Отрасль 1 Отрасль 2 Отрасль 3	Валовый продукт
Отрасль 1 Отрасль 2 Отрасль 3	4 6 6 10 10 4 6 4 6	100 70 60

     Найти конечный продукт каждой отрасли, чистую продукцию каждой отрасли, матрицу коэффициентов прямых затрат. Какой будет валовой продукт каждой отрасли, если конечный продукт первой отрасли необходимо увеличить на 50 %, второй уменьшить на 7 единицы, а третьей увеличить на 10 единиц.

Лекция 4. Задача линейного программирования 

Математическая модель задачи состоит из следующих элементов.

1. Целевая функция (критерий оптимальности) - может быть на нахождение максимального значения (прибыль предприятия) или минимального значения (себестоимость, затраты).

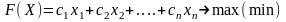
2. Ограничения задачи. Задаются виде уравнений или неравенств.

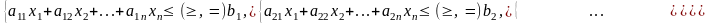
3. Условия неотрицательности переменных. Неизвестные переменные за-

дачи отражают некоторые реальные параметры экономической системы,

которые, как правило, не могут принимать отрицательных значений, поэтому соответствующие неизвестные переменные должны быть положительными или нулевыми.

Допустимое решение — это совокупность чисел (план)

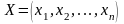
Оптимальное решение

— это план, при котором ЦФ принимает свое максимальное

(минимальное) значение.

Задача 4.1. Для изготовления различных изделий A и B используется 2 вида сырья.

На производство единицы изделия A требуется затратить сырья:

1-го вида -15кг, 2-го вида - 11кг, 3-го вида - 9кг.

На производство единицы изделия B

требуется затратить сырья 1-го вида - 4кг, 2-го вида - 5кг, 3-го вида - 10кг.

Производство обеспечено сырьем

1-го вида в количестве 1095кг, 2-го вида - 865кг, 3-го вида -1080кг.

Прибыль от реализации

единицы готового изделия А составляет 3$, изделия B - 2 $.

Составить план производства изделий А и В, обеспечивающий максимальную прибыль от их реализации.

Решение:

Указанная задача может быть либо решена в Excel (функция Поиск решения) либо с помощью математического облачного сервиса (например WA).

Задача 4.2.: Фармацевтическая фирма ежедневно производит не менее 800 кг некой пищевой добавки, которая состоит из смеси кукурузной и соевой муки, состав которой представлен в следующей таблице

Мука	Белок, кг на кг муки	Клетчатка, кг на кг муки	Стоимость ($./кг)
Кукурузная	0,09	0,02	0,3
Соевая	0,6	0,06	0,9

Диетологи требуют, чтобы в пищевой добавке было не менее 30% белка и не более 5% клетчатки.

Фирма хочет определить рецептуру смеси наименьшей стоимости с учетом требований диетологов.

Решение:

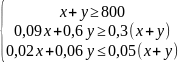
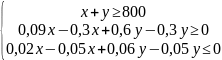
Задача 4.3 Компания поставляет фруктовые соки и напитки (смеси соков). Список продукции фирмы и цена за литр приведены в таблице:

	Цена за литр
Яблочный сок	40
Виноградный сок	42
Клюквенный сок	37
Яблочно-виноградный	40
Яблочно-клюквенный	39
Фруктовая смесь	42

Состав смесей: яблочно-виноградный – 70% яблочный сок и 30% виноградный сок, яблочно-клюквенный – 60% яблочный сок и 40% клюквенный сок, и фруктовая смесь – 50% яблочный сок, 20% виноградный сок и остальное - клюквенный сок.

В настоящий момент на складе компании имеется 3000 литров яблочного сока, 1900 литров виноградного сока, и 2500 литров клюквенного сока. Менеджер хочет выяснить, сколько пакетов каждого изделия нужно выпустить, чтобы максимизировать прибыль. Себестоимость литра яблочного сока – 20 руб., виноградного сока – 23 руб. и клюквенного сока – 18 руб. Все напитки упакованы в стандартные пакеты емкостью 1 литр.

Компания имеет заказ на 600 пакетов яблочного сока, 300 пакетов яблочно-виноградного сока и 1000 пакетов фруктовой смеси. Заказ должен быть выполнен в текущую поставку. Опыт показывает, что ни один из видов продукции не следует производить в количестве более чем 2000 пакетов.

Составьте план розлива, дающий наибольшую прибыль в сложившейся

ситуации.