Основна теорема арифметики
Будь-яке натуральне число більше одиниці може бути розкладене в добуток простих співмножників і це розкладання єдине, якщо не враховувати порядок слідування співмножників.
Доведення
Існування.
Нехай а > 1, а N. Тоді число а має простий дільник, позначивши який через р1 дістанемо:
а = р1 · а1
Якщо а1 > 1, то аналогічно попередньому:
а1 = р2 · а2, де р2 – просте число и т.д.
Оскільки а > а1 > а2 > …, то після скінченного числа кроків дістанемо ап = 1, отже:
а = р1· р2 …· рп (1)
Це і є шукане розкладання натурального числа а >1 на прості співмножники.
Єдиність .
Доведемо методом від супротивного, припустивши, що для числа а > 1; а N існує ще одне крім (1) розкладання на прості співмножники.:
а = q1 ·q2 ·…· qm (2)
З (1) і (2) випливає рівність:
р1· р2 · …· рп = q1 ·q2 ·…· qm (3)
Звідси випливає, що добуток р1 ∙ р2 …рп ділиться на просте число q1, значить, на q1 ділиться один із співмножників р1 ∙ р2 ∙ …∙ рп. Нехай р1 q1, але враховуючи, що обидва числа прості, маємо: р1 = q1.
Скоротивши на р1 = q1 обидві частини рівності (3), одержимо:
р2 · …· рп =·q2 ·…· qm
Після скінченної кількості кроків скоротяться всі співмножники в одній частині рівності (3), наприклад у лівій. Якщо в іншій частині рівності при цьому скоротилися не всі співмножники, прийдемо до неможливої рівності:
1 = qп+1 ·…· qm, бо qп+1 ,…, qm – прості числа.
Одержана суперечність свідчить про хибність зробленого припущення, тобто про істинність твердження про єдиність розкладання.
У розкладанні натурального числа а >1 деякі співмножники можуть повторюватись. Нехай р1, р2, …, рк – різні співмножники цього розкладання і нехай рі входить співмножником αі раз (і = 1, 2,…, k).
Тоді а = р
р
·
… ·р
Це – так зване канонічне розкладання натурального числа а > 1.
Наприклад:
14520 7260 3630 1815 605 121 11 1 |
2 2 2 3 5 11 11
|
14520 = 23 · 3 · 5 · 112 |
Найменше спільне кратне та найбільший спільний дільник,
їхні властивості і алгоритми знаходження.
Натуральне число а ділиться на натуральне число b, якщо існує таке натуральне число q, що а = bq. При цьому в називається дільником числа а , а число а – кратним числа b.
Найменшим спільним кратним даних чисел а1, а2, …ап називається найменше число, що ділиться на всі дані числа: К (а1, а2, …ап).
Найбільшим спільним дільником даних чисел а1, а2, …ап називається найбільше число, на яке діляться всі дані числа: D (а1, а2, …ап).
Властивості НСК
НСК натуральних чисел а і b завжди існує і єдине.
К (а;b)
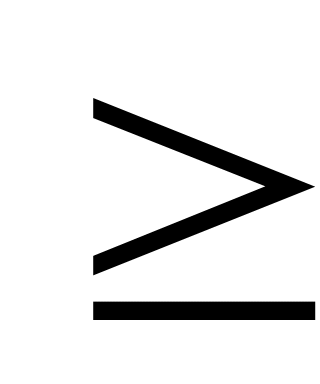а, якщо а
>
b
(НСК не менше більшого з даних чисел).Будь-яке спільне кратне даних чисел ділиться на їхнє найменше спільне кратне.
Властивості НСД
НСД натуральних чисел а і b завжди існує і єдине.
D (а;b)
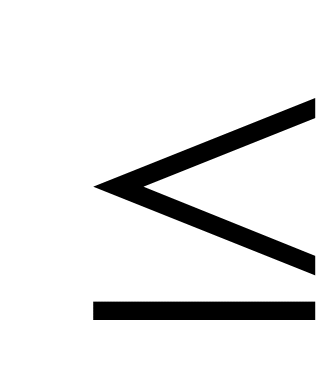а, якщо а
<
b
(НСД не більше меншого з даних чисел).Найбільший спільний дільник даних чисел ділиться на будь-який їхній спільний дільник
Теорема.
НСК двох даних чисел дорівнює їхньому добутку, поділеному на НСД цих чисел:
К(а;b)
=
або
К(а;b)·D(a;b)
= ab.
Алгоритм знаходження НСК
Щоб знайти НСД даних чисел треба:
Представити всі дані числа у вигляді канонічного розкладання.
Знайти добуток всіх простих співмножників, що є в розкладаннях, взятих з найбільшим показникам, з яким вони входять в усі розкладання.
Алгоритм знаходження НСД
Щоб знайти НСД даних чисел треба:
Представити всі дані числа у вигляді канонічного розкладання.
Знайти добуток спільних простих співмножників, що є в розкладаннях, взятих з найменшим показником, з яким вони входять в усі розкладання.
Наприклад: D (504; 540) - ? K (504; 540) - ?
504 252 126 63 21 7 1 |
2 2 2 3 3 7
|
|
540 270 135 45 15 5 1 |
2 2 3 3 3 5 |
D(504; 540) = 22·32 = 4·9=36 K(504; 540) = 23·33 · 5·7=7560
|
504= 23·32·7 540 = 22·33·5
На відміну від НСК, НСД двох даних чисел може бути знайдений без виконання канонічного розкладання, а за так званим алгоритмом Евкліда:
D (504; 540) - ?
5
04
1
504 36
Д (540; 504)
1
4
144
1 44
0
В цьому разі найбільшим спільним дільником буде остання відмінна від нуля частка, або останній дільник.
Застосування НСК на практиці – при зведенні дробів до спільного знаменника, а НСД – при скороченні чисельника і знаменника дробу.