Відношення подільності на множині натуральних чисел, його властивості. Чотири класи невід’ємних цілих чисел. Теорема про нескінченність множини простих чисел.

Число а ділиться на число в ≠ 0, якщо існує їхня частка, тобто таке натуральне число q, що a = вq. Записується: а в.

Властивості відношення подільності.

1. Рефлексивність:

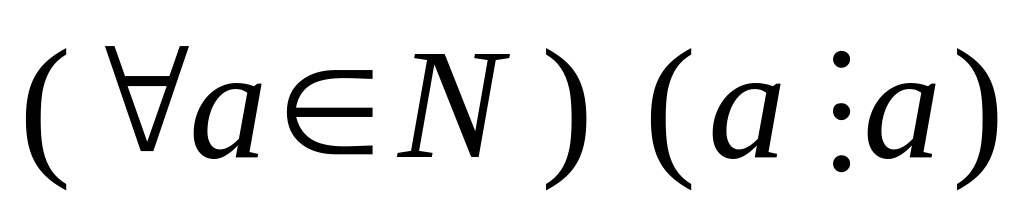
Доведення випливає з рівності

2. Антисиметричність:

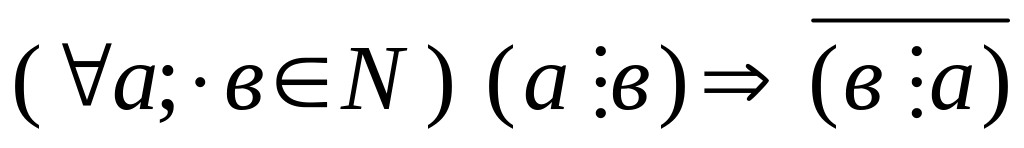
а ≠ в

Доведення – методом від супротивного.

3. Транзитивність: (

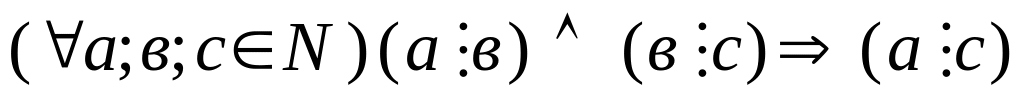
Доведення:

;

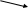позначимо q

Висновок: відношення подільності є відношенням нестрогого порядку.

Теорема про подільність суми.

Якщо кожне з натуральних чисел а₁;…; а_п ділиться на натуральне число в, то їхня сума а₁ +_…+ а_п теж ділиться на в.

Теорема про подільність різниці.

Якщо числа а₁ і а₂ діляться на в і а₁ ≥ а₂, то їхня різниця (а₁ – а₂) ділиться на в.

Теорема про подільність добутку.

Якщо число а ділиться на в, то добуток ах, де , теж ділиться на в.

Доведення:

Натуральне число, більше 1 називається простим, якщо воно ділиться тільки на 1 і на себе.

Наприклад: 2; 3; 5; 7; 11; 13; 17; 19, … – прості числа.

Натуральне число, більше 1 називається складеним, якщо в нього більше двох дільників.

Наприклад: 1) 4 1; 2; 4. 2) 12 1; 2; 3; 4; 6; 12.

Число 0 ділиться на всі натуральні числа. Отже, всі невід’ємні цілі числа можна класифікувати за числом їхніх дільників:

1. Число 1 – має лише один дільник.

2. Прості числа – мають рівно два дільники.

3. Складені числа – мають більше двох дільників.

4. Число 0 – має нескінченну кількість дільників.

Теорема Евкліда

Множина простих чисел нескінченна.

Доведення (методом від супротивного).

Припустимо, що множина простих чисел скінченна, тобто існує найбільше просте число Р.

Розглянемо число х = 2 ∙ 3 ∙ 5 ∙ …∙Р + 1.

Воно – складене, оскільки більше від Р . Значить, воно має ділитись на одне з простих чисел від 2 до Р (крім, звичайно, 1 і самого себе). Це ділення неможливе, бо завжди буде залишатись остача 1. Одержана суперечність свідчить про хибність припущення, а значить, про істинність теореми.

Ознаки подільності на 2; 3; 4; 5; 9; 25. Ознака подільності на складене число

Ознака подільності – це твердження, яке зводить питання про подільність будь-якого натурального числа на задане число т до питання про подільність на т деякого меншого натурального числа.

Теорема (ознака подільності на 2(5)).

Натуральне число ділиться на 2(5) тоді і тільки тоді, коли на 2(5) ділиться остання цифра в запису даного числа.

Доведення:

Нехай а = а_п• 10^п + а_п-1• 10^п-1 + …+ а₂ • 10² + а₁ • 10¹ + а₀ , де а_п 0.

Враховуючи, що 10 = 2 · 5 2(5), винесемо за дужки спільний множник 10 де це можливо:

а = 10 · (а_п · 10^п-1 + а_п-1 · 10^п-2 + …+ а₁) + а₀.

2(5)

2(5) за Теоремою про подільність добутку

Значить, за теоремою про подільність суми і різниці, для подільності числа а на 2(5) необхідно і достатньо, щоб а₀ 2(5).

Теорема (ознака подільності на 4(25)).

Натуральне число ділиться на 4(25) тоді і тільки тоді, коли на 4(25) ділиться число, утворене двома останніми цифрами в запису даного числа.

Доведення (аналогічно попередньому).

Теорема (ознака подільності на 9(3)).

Натуральне число ділиться на 9(3) тоді і тільки тоді, коли на 9(3) ділиться сума цифр даного числа.

Для доведення покажемо, спочатку, що (10^п – 1) 9(3).

Застосуємо метод математичної індукції:

І. Доведемо, що А(1) – і: 10¹ – 1 = 10 – 1 = 9 9(3) – істинно.

ІІ. Припустимо, що А(к) – і : (10^к – 1) 9(3) – істинно.

ІІІ. Доведемо, що (А(к) – і) (А (к+1) – і), тобто (10^к – 1) 9(3) (10^к+1-1) 9(3).

1 0^к+1– 1 = 10^к · 10¹ – 1 = 10 · 10^к – 1 = (1+9) · 10^к – 1 = 10^к + 9 · 10^к – 1 = = (10^к – 1) + 9 · 10^к.

9(3) за 9(3)

припущенням

в п.ІІ 9(3) за Т. про

подільність добутку

9(3) за Т. про подільність суми

Висновок: (10^п – 1) 9(3)

Основний етап доведення: Нехай а = а_п · 10^п + а_п-1 · 10^п-1 + …+ а₂ · 10² + а₁ · 10¹ + а₀.

Віднімемо від обох частин цієї рівності в = а_п + а_п-1 + …+ а₂ + а₁ + а₀.

а – в = (а_п · 10^п + …+ а₁ · 10¹ + а₀) – (а_п+ …+ а₁ + а₀) = (а_п · 10^п – а_п) + …+ (а₁ ·10¹ – а₁) + (а₀ – а₀) = а_п · (10^п – 1) + …+ а₁ (10¹ – 1)

Останній вираз ділиться на 9(3), бо кожен з доданків містить множник, який ділиться на 9(3), тоді для подільності числа а на 9(3) необхідно і достатньо, щоб на 9(3) ділилось число в = а_п + а_п-1 + …+ а₂ + а₁ + а₀ – сума цифр даного числа.

Наприклад:

1. 315 9 і 3, бо 3 + 1 + 5 = 9 9(3) і на 5 – бо остання цифра ділиться на 5.

2. 2700 4(25), бо останні дві цифри – нулі.

3. 396 9, 3, 2, 4, бо 3+9+6 = 18 9(3); 6 2; 96 4.

Теорема

Якщо два даних числа взаємно прості, то для подільності третього числа на їхній добуток необхідно і достатньо, щоб це число ділилось на кожне з даних чисел.

(

Наприклад: Для подільності натурального числа на 15 необхідно і достатньо, щоб воно ділилось на 3 і на 5, тобто щоб сума цифр ділилась на 3, а остання цифра була 5 або 0.

247321425 15, бо остання цифра 5, а 2+4+7+3+2+1+4+2+5 = 30 3.