Множини і операції над ними (об’єднання, переріз, різниця, доповнення, декартовий добуток). Властивості операцій.
Теорія множин – це розділ математики, що вивчає множини, абстрагуючись від конкретної природи їхніх об’єктів. Поняття множини – одне з найважливіших у математиці. Вводиться воно без означення через інші поняття. Під множиною об’єктів розуміють сукупність, клас, набір, колекцію і т.д., наприклад: множина людей, множина частин мови, множина натуральних чисел, множина дійсних коренів квадратного рівняння ах2 + вх + с = 0 (а ≠0).
Розглядаючи останню множину, зауважимо, що в залежності від дискримінанта Д вона має 2 дійсних корені (Д > 0), 1 дійсний корінь ( Д=0) або не має жодного дійсного кореня (Д<0), тоді кажуть, що це – порожня множина (Ø).
Об’єкти, що
складають множину,
називаються її елементами. Запис
множини і її елементів за допомогою
символіки: А={а1; а2;…;
ап} -
множина А складається з елементів
а1;,а2, …,
ап.; а1
А
– елемент а1
належить множині А,
в
А
(або в
А)
– елемент в
не належить множині А.
Способи задання множин: 1. Переліком всіх її елементів (для скінченних множин) А={0; 1; 2 3; 4; 5; 6; 7; 8; 9} - множина цифр десяткової системи числення.
2. Описом
або показом характеристичних властивостей
(як для скінченних, так і для нескінченних
множин) Х= {х / х
N;
х
2}-
множина парних натуральних чисел.
Множина В
називається підмножиною множини А,
якщо всі елементи множини В є
елементами множини А: В
А або А
В
– символічний запис.
Множини А і В називаються рівними, якщо вони складаються з одних і тих же елементів, тобто якщо А є підмножиною В, а В – підмножиною А.
Для наочного зображення множин і відношень між ними використовують круги Ейлера. Можливі варіанти відношень між двома множинами:
Операції над множинами
1
.
Об’єднання множин А і В –
це така операція, результатом якої є
множина А
В, що складається з елементів, які
входять хоча б до однієї з вихідних
множин:
А В = х / х А або х В
2
.
Перетин
множин А і В – це така операція,
результатом якої є множина А 
В, що складається з елементів, які
входять до обох вихідних множин (тобто
є спільними):
А В = х / х А і х В
А
В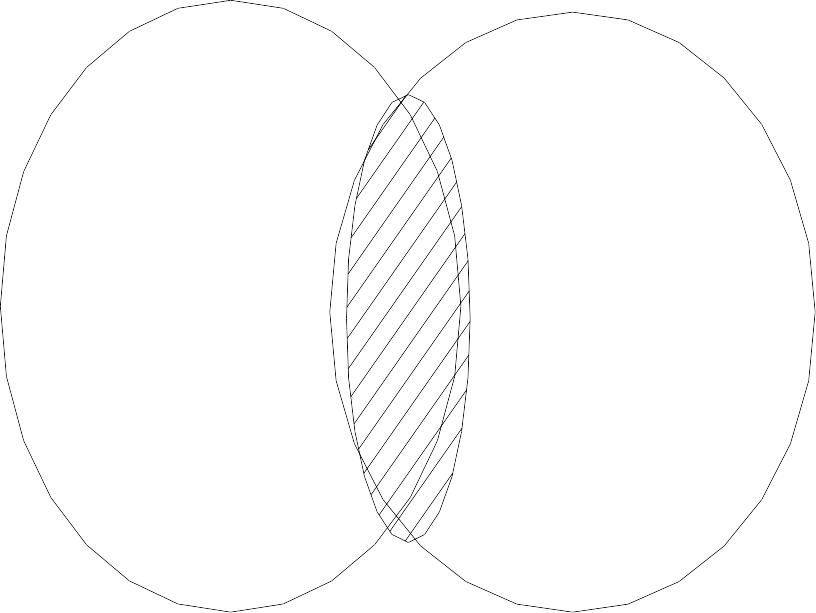
3. Різниця
множин А і В –
це така операція, результатом якої є
множина А \ В, що складається з
елементів множини А, які
не входять до множини
В:
А \ В= х / х А, х В
4
.
Якщо В
А, то доповнення В до множини
А – це така операція, результатом
якої є множина В
(
),
що складається з елементів множини
А, які не входять до
множини В:
В
А, то В
=
х / х
А,
х
В
Доповнення – окремий випадок різниці.
5
.
Декартовий (прямий) добуток множин
А і В – це така операція,
результатом якої є множина А
В, що складається з пар виду (а; в),
де а
А, в
В:
А В = (а; в) / а А; в В
Наприклад: А = { a; b; c; d} ; В = {d ; e}
А В = {a; b; c; d; e}, А В = { d}
А \ В = {a; b; c}; В | А= {e}
А
=
В
=
Ø , бо А
В,
В
А
А В = {(a; d); ( a; e); ( b; d); ( b; e); ( c; d); ( c; e); ( d; d); ( d; e)}
В А = {(d; a); ( e; a); (d; b); ( е; b); ( d; c); ( е; c); ( d; d); ( e; d)}.