4. Отражательные дифракционные решётки

На пропускающих дифракционных решётках, штрихи у которой нанесены на прозрачную (стеклянную) поверхность, интерференционная картина образуется в проходящем свете. На отражательной дифракционной решётке штрихи нанесены на зеркальную (металлическую) поверхность, и результирующая интерференционная картина образуется в отражённом от решётки свете.

Эшелетт (франц. echelette, от echelle — лестница) – отражательная дифракционная решетка, способная концентрировать дифрагированное излучение в спектре одного порядка, ослабляя остальные, в том числе и самый яркий спектр нулевого порядка. Изменения распределения излучения по спектрам и высокой концентрации энергии в узкой спектральной области достигают, вводя дополнительную разность хода в пределах каждого отдельного штриха, имеющего, как правило, треугольный профиль. Отражательные решётки типа Эшелетт обычно нарезают специальными резцами на металлической поверхности (медь, латунь, алюминий) и используют для наблюдения спектров 5—10 порядков в инфракрасной области. Возможно также создание Эшелеттов для видимой и ультрафиолетовой спектральных областей.

В последние годы в связи с успехами лазерной техники и голографии открылись возможности голографического изготовления дифракционных решеток. Такая решетка представляет собой зарегистрированную на светочувствительном материале интерференционную картину, образованную двумя когерентными пучками света. Картина может быть зарегистрирована в виде модуляции коэффициента поглощения, отражения или показателя преломления при этом соответственно образуется амплитудная, фазовая решетка с синусоидальным профилем штрихов. Меняя форму интерферирующих волновых фронтов, голографической решетке можно придавать любые свойства, например, получать плоские решетки, лишённые астигматизма.

До недавнего времени распространение дифракционных решеток ограничивалось сложностью делительных машин, создание которых было доступно лишь немногим странам. Высокая стоимость и малая производительность этих машин определяет и большую стоимость дифракционных решеток. Положение существенно изменилось после того, как были усовершенствованы методы получения копий дифракционных решеток (реплик). Интересно отметить, что качество реплик иногда оказывается даже выше качества оригинальной решетки. Это объясняется тем, что пластмасса плохо передает мелкие дефекты штриха и последний на реплике получается более гладкими, чем он был на оригинальной решетке. После изготовления реплики покрывают отражающим слоем.

Плоские отражательные дифракционные решёткиизготавливаются путем нарезки алмазным резцом мягкой металлической поверхности. Основанием для решетки служат обычно стеклянные заготовки с большой точностью полировки. На заготовку наносится испарением слой хрома, поверх него слой алюминия, по которому и ведется нарезка. Необходимый профиль штриха и наклон его отражающих граней достигается соответствующим углом заточки и установки режущего алмаза. Они имеют прямолинейные, строго параллельные друг другу и эквидистантные(расположенный на одинаковом расстоянии) штрихи одинаковой формы. Такая дифракционная решётка представляет собой периодическую структуру с постоянным расстоянием d между штрихами (рис. 4.1), которое называется периодом дифракционные решётки. Различают амплитудные и фазовые дифракционные решётки. У первых периодически изменяется коэффициент отражения или пропускания, что вызывает изменение амплитуды падающей световой волны (такова решётка из щелей в непрозрачном экране). У фазовыхдифракционные решётки штрихам придаётся специальная форма, которая периодически изменяет фазу световой волны.

Рис. 4.1. Схема одномерной периодической структуры плоской дифракционной решётки: d - период решётки; W - длина нарезной части решётки.

Рис. 4.2(Схема, иллюстрирующая принцип действия фазовой отражательной дифракционной решётки): d - постоянная решётки, а - ширина щели, i - угол "блеска",  - угол падения,  - угол дифракции, N — нормаль к общей поверхности эшелетта; N'— нормаль к зеркальной грани штриха, α – угол падения на грань штриха, β – угол дифракции от грани штриха.

Фазовая дифракционная решётка представляют собой регулярную последовательность канавок определённого профиля, в данном случае треугольного (Рис. 4.2). Рабочая широкая грань называется зеркальным элементом и ее поверхность выполняется очень качественно. Особенностью работы таких решеток является то обстоятельство, что для длины волны , зеркально отражающейся от рабочей грани штриха, имеет место максимальная концентрация энергии. Причем положение этого максимума можно смещать по спектру, изменяя угол i профиля штриха.

Рассмотрим действие профилированной решётки, изображённой на рис.4.3. Параллельный пучок лучей, падающий по направлению ѱ, дифрагирует на структуре решётки. Каждой монохроматической волне сложного состава излучения соответствует определённы угол дифракции . Введём правило знаков для углов: углы положительны, если они расположены по одну сторону от нормали по ходу часовой стрелки. В соответствии с этим на рисунке угол положителен, а угол отрицателен. Кроме того, все порядки спектров m положительны, если они расположены от нулевого порядка по ходу часовой стрелки.

В отражательной решётки функция U из формулы (1) представляется в виде:

Здесь – i) – проекция рабочей грани штриха на поверхность фронта падающей волны(соответствует ширине прозрачной части штриха решётки, работающей на пропускание).

Главный максимум при дифракции от отдельного зеркального элемента имеет место при , так как в этом случае I(0)=1. Тогда угол дифракции . Он соответствует зеркальному отражению света от рабочей грани штриха, когда α=β.

Учёт выражения –β = даёт следующую формулу:

sin + sin = /a, (2)

которое при известном профиле штриха позволяет вычислить его ширину а (рассматриваем в главном порядке).

Второй множитель в (1) здесь так же, как и в случае прозрачной решётки, определяет интерференцию N пучков. Для отражательной решётки / ].

Условие главных максимумов для непрофилированной решётки (i=0) можно представить в виде:

(3)

гдеm = 0, 1, 2, 3,… - порядок спектра.

Для решетки с углом блеска (i≠0) выражение 3 принимает следующий вид:

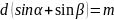, (4)

Гдеα=ψ– i, β = φ –i

Между главными максимумами, как следует из теории решётки, будет располагаться N-1 минимум, количество минимумов очень велико, и так как в рамках нашей задачи они нам не нужны, рассматривать их не будем.