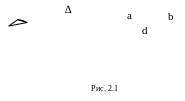ЦЕЛЬ РАБОТЫ: Определение основных параметров дифракционной решётки.
ОБЪЕКТ ИССЛЕДОВАНИЯ: Объектом исследования в данной лабораторной работе является отражательная дифракционная решётка.
ЗАДАЧИ РЕШАЕМЫЕ В РАБОТЕ:
Ознакомление с основными характеристиками дифракционных решёток..
Экспериментальное определение основных параметров дифракционной решётки.
СВЕДЕНИЯ ИЗ ТЕОРИИ:
1. Дифракция на щели.
Пусть на бесконечную длинную узкую щель шириной а нормально падает плоская монохроматическая световая волна (Рис. 1.1). Разобьём часть волновой поверхности, находящейся в области щели, на ряд мелких параллельных полос равной ширины(зоны Френеля). Каждая из этих полос в соответствии с принципом Гюйгенса-Френеля может являться вторичным источником волн, при этом фазы всех этих волн одинаковы, так как при нормальном падении на плоскость щель совпадает с фронтом волны.
Разность хода лучей - разность длин путей двух световых лучей, имеющих общие начальную и конечную точки: Δ=a·sin(φ), где Δ- разность хода. Оптическая разность хода отличается от данной умножением на коэффициент преломления среды.
Ширина каждой зоны Френеля выбирается такой, чтобы оптическая разность хода между крайними лучами была равна половине длины волны.
|
В
направлении
 = 0, щель действует как одна зона Френеля,
и в этом направлении интенсивность
света максимальна. Распределение
интенсивности на экране, полученное
вследствие дифракции (дифракционная
картина), наблюдаемое на большом
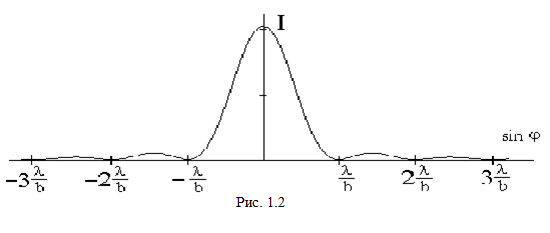
расстоянии от щели представлено на рис.
1.2.
= 0, щель действует как одна зона Френеля,
и в этом направлении интенсивность
света максимальна. Распределение
интенсивности на экране, полученное
вследствие дифракции (дифракционная
картина), наблюдаемое на большом
расстоянии от щели представлено на рис.
1.2.
Интенсивность изменяется по закону:

где I0 - интенсивность света, идущего от щели, шириной а в направлении первичного пучка.
|
Центральны максимум будет общим для всех длин волн, так что центр дифракционной картины представится в виде белой полоски, переходящей в цветную каёмку. Вторичные максимумы для разных длин волн уже не совпадают между собой: ближе к центру располагаются максимумы, соответствующие более коротким волнам. Длинноволновые максимумы отстоят друг от друга дальше, чем коротковолновые. Однако максимумы эти настолько расплывчаты, что никого сколько-нибудь отчётливого разделения различных длин волн (спектрального разложения) при помощи дифракции на одной щели получить нельзя.
2. Дифракция от двух щелей.
Пусть на диафрагму с двумя одинаковыми параллельными друг другу щелями шириной а (расстояние между щелями равно b, а + b = d) падает плоская световая волна(рис. 2.1). Щели дадут две одинаковые, накладывающиеся друг на друга дифракционные картины. При некогерентном освещении максимумы будут усиливаться, так как их положение определяется лишь направлением дифрагированного света, и распределение интенсивности не будет отличаться от случая одной щели.
|
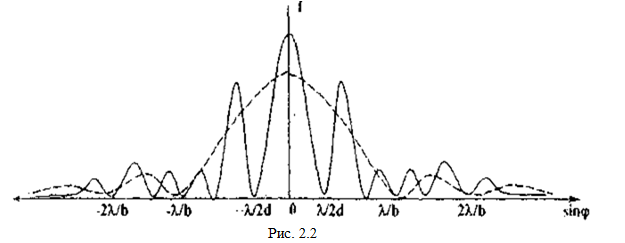
Если освещение когерентное, то полученная картина усложняется вследствие взаимной интерференции волн, идущих от первой и второй щелей (Рис. 2.2).
|
Кроме того, вследствие взаимной интерференции световых лучей, посылаемых двумя щелями, в некоторых направлениях они будут гасить друг друга, что приведет к возникновению дополнительных минимумов. Эти минимумы будут наблюдаться в тех направлениях, которым соответствует оптическая разность хода лучей (Δ= CF = (a+b) sin(φ) = dsin(φ), кратная λ/2.
Таким образом, условие дополнительных интерференционных минимумов имеет вид:
dsin(φ)= ±(2m+1)λ/2 (m = ±1,±2,..,)
Наоборот, действие одной щели будет усиливать действие другой, если оптическая разность хода лучей кратная λ, то есть в данном направлении будут наблюдаться интерференционные максимумы, если:
dsin(φ) = ±mλ (m = ±1, ±2,...,)
Из этих условий видно, что между двумя первыми главными минимумами от одной щели располагаются интерференционные максимумы и минимумы от двух щелей. Расстояние между главными минимумами зависит от ширины щели а. Если расстояние между щелями значительно больше их ширины b>> а (узкие щели), то между прежними минимумами (от одной щели), может располагаться значительное количество минимумов и максимумов.