Лекция 2.2 Частотный критерий Найквиста (разомкнутая система нейтральна , разомкнутая система неустойчива).

Пусть разомкнутая система нейтральна. ПФ разомкнутой системы в этом случае содержит некоторое количество нулевых полюсов, а все остальные полюса являются "левыми". АФЧХ такой системы имеет разрыв при нулевой частоте

В этом случае критерий устойчивости формулируется так:

Для устойчивости замкнутой системы необходимо и достаточно, чтобы АФЧХ разомкнутой системы, при изменении частоты от нуля до бесконечности, дополненная на участке разрыва дугой бесконечно-большого радиуса, не охватывала точку с координатами (-1,j0).

Дополнение дугой бесконечно-большого радиуса осуществляется по часовой стрелке от направления положительной вещественной полуоси на угол, определяемый произведением 90 градусов на число нулевых полюсов разомкнутой системы.

Для примера, рассмотрим наиболее типичный случай реальной системы с одним нулевым полюсом. АФЧХ разомкнутой системы приведена на Рис. Соответствующие ей ЛАЧХ и ФЧХ показаны на Рис.

На Рис. и Рис. показаны примеры устойчивой замкнутой системы при наличии двух и трех нулевых полюсов в ПФ разомкнутой системы.

Рассмотрим случай нейтрально-устойчивой разомкнутой системы (реально соответствует разомкнутой системе, содержащей звенья с очень малым демпфированием).

Пусть ПФ разомкнутой системы содержит пару мнимых полюсов. АФЧХ такой разомкнутой системы имеет разрыв, так как включает консервативное звено. Для использования критерия в известном виде, необходимо ликвидировать разрыв годографа, замкнув его дугой бесконечно-большого радиуса. Пример показан на Рис..для ПФ разомкнутой системы, имеющей вид:

Разомкнутая система неустойчива. Правило переходов, как общий способ оценки устойчивости по критерию Найквиста

Рассмотрим наиболее неблагоприятный случай, когда разомкнутая система неустойчива (характеристическое уравнение разомкнутой системы имеет правые полюса).

Практически такая ситуация возникает при наличии в системе внутренних неустойчивых контуров. Заметим, что при проектировании системы разработчик в большинстве случаев (в интересах отладки системы) стремится реализовать внутренние контуры с достаточной гарантией устойчивости. Однако, такие контуры могут возникнуть в процессе эксплуатации системы при изменении параметров, причем заранее учесть эти изменения сложно (например, изменение характера аэродинамической нагрузки на рулевые поверхности ЛА).

Для применения критерия Найквиста необходимо заранее определить количество "правых" полюсов ПФ разомкнутого контура. Если ПФ разомкнутого контура представляет произведение ПФ звеньев не выше второго порядка, то количество "правых " полюсов равно суммарному порядку всех неминимально-фазовых звеньев (полиномы их ПФ содержат отрицательные коэффициенты). В общем случае необходимо найти корни характеристического уравнения разомкнутого контура и подсчитать сумму тех из них, которые содержат положительные действительные части.

В первично виде (не очень удобном для применения) критерий Найквиста формулировался следующим образом:

Если разомкнутая система неустойчива и содержит "r" правых полюсов, то для устойчивости замкнутой системы необходимо и достаточно, чтобы при изменении частоты от нуля до бесконечности, АФЧХ разомкнутой системы охватывала точку с координатами (-1,j0) "r/2" раз при движении изображающей точки с ростом частоты в положительном направлении ( против часовой стрелки).

Для анализа сложных годографов подсчет "охватов" представляет затруднения. Более конкретный и формализованный вид имеет формулировка критерия, основанная на понятии "переход". Эта формулировка носит название правила "переходов". В дальнейшем будем пользоваться этим правилом.

Под "переходом" понимается факт пересечения годографом (АФЧХ) отрезка действительной оси на интервале значений от -1 до - . Факт пересечения конкретизирован числом. Если годограф, с ростом частоты, пересекает данный отрезок сверху вниз (движение в область меньшего фазового сдвига), то ему присваивается число +1.Если - в обратную сторону, то -1. Если годограф начинается (даже в бесконечности) с фазового угла -180 градусов и с ростом частоты фазовое отставание растет, то -1/2, если уменьшается, то +1/2. Возможные варианты приведены на Рис.

Правило переходов формулируется в виде:

Замкнутая система устойчива, если алгебраическая сумма переходов равна "r/2",где "r" - число правых полюсов разомкнутого контура.

При наличии разрывов годографа, вызванных наличием нулевых полюсов в ПФ неустойчивой разомкнутой системы, разрывы ликвидируются с помощью дуги бесконечно большого радиуса. При этом отсчет дуги бесконечно большого радиуса осуществляется от верхнего ближайшего к начальному значению ФЧХ уровня нечетно- кратного -180 градусам (-180,-540,-900 и т.д). Переходы фиксируются на всех пересекаемых уровнях нечетно-кратных значению -180 градусов.

При использовании ЛЧХ правило переходов сохраняет свой смысл. Фиксация переходов происходит в точках пересечения ФЧХ (с учетом ее дополнения при наличии разрывов) уровней нечетно-кратным -180 градусам. Переходы подсчитываются на этих уровнях для тех частотных диапазонов, где ЛАХ лежит выше оси частот.

На Рис. приведены ЛЧХ разомкнутой системы с ПФ вида:

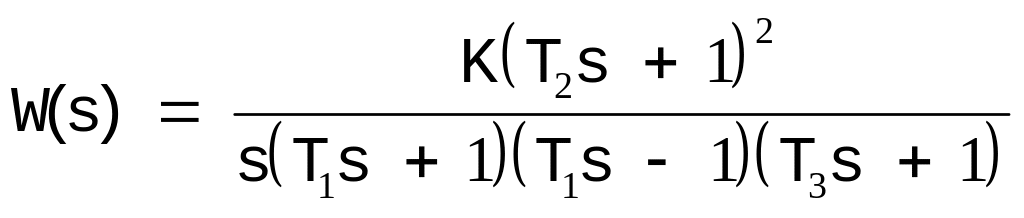
Разомкнутая система неустойчива. Имеет один правый и один нулевой полюс. Начальное значение ФЧХ -270 градусов. Дополнение ФЧХ на участке разрыва от ближайшего уровня - 180 градусов. Сумма переходов считается на двух уровнях и равна -1/2,что соответствует устойчивой замкнутой системе.

Данным ЛЧХ соответствует годограф, показанный на Рис..

На Рис. приведены ЛЧХ разомкнутой системы с ПФ вида:

W(s)=

Разомкнутая система неустойчива. ПФ содержит один правый полюс. Начальное значение ФЧХ -180 градусов. Разрывы годографа отсутствуют. Сумма переходов считается на одном уровне (-180 градусов) и равна +1/2,что соответствует устойчивой замкнутой системе.

Правило переходов является справедливым и при отсутствии правых полюсов, что дает возможность применять его для рассмотренных выше случаев (разомкнутая система устойчива, разомкнутая система нейтральна и нейтрально-устойчива). Согласно правилу формулировка критерия имеет вид:

Если разомкнутая система устойчива, то для устойчивости замкнутой необходимо и достаточно, чтобы сумма переходов равнялась нулю.

При этом переходы подсчитываются на одном уровне ФЧХ, равном -180 градусов и в диапазонах частот, где ЛАХ лежит выше оси частот.

При наличии нулевых полюсов в ПФ разомкнутой системы, разрывы АФЧХ при нулевой частоте ликвидируются с помощью дуги бесконечно-большого радиуса, проводимой от положительного направления действительной оси на число квадрантов, равное числу нулевых полюсов по часовой стрелке.

На Рис. показаны ЛАХ и АФЧХ характеристики разомкнутой условно-устойчивой системы, имеющей нулевой полюс. Дополнение дугой радиуса равного бесконечности дает сумму переходов равную нулю. Система с такой характеристикой устойчива. Это подтверждается формулировкой критерия для второго варианта.

На Рис. показаны характеристики устойчивой разомкнутой системы, содержащей слабодемпфированное звено. Система неустойчива.

На Рис. показаны характеристики разомкнутой системы, содержащей три нулевые полюса. Дополнение дугой радиуса равного бесконечности приводит к появлению еще одного перехода противоположного знака . Система устойчива.