Алгебраический критерий устойчивости Гурвица.
В основе критерия лежит анализ диагональных определителей матрицы Гурвица.
Пусть характеристическое уравнение системы в целом приведено к виду:
Матрица Гурвица составляется из коэффициентов уравнения в последовательности:
- по диагонали матрицы
записываются коэффициенты уравнения
начиная с коэффициента
и кончая коэффициентом
-каждый столбец матрицы получается дополнением диагонали вверх и вниз, вверх индексы коэффициентов растут, вниз последовательно уменьшаются;
-при отсутствии в уравнении какого-либо коэффициента и вместо коэффициентов с индексами меньше нуля и больше "n" записывается ноль.
Например ,для системы четвертого порядка, получаем:
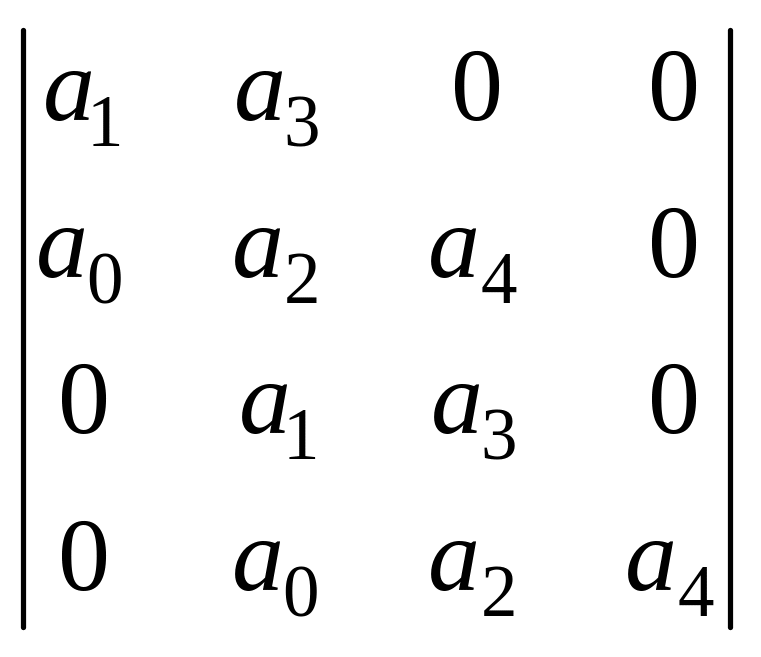
Система устойчива, если ,при положительности всех коэффициентов характеристического уравнения системы, все диагональные определители положительны. Например:
Система является
нейтрально -устойчивой, если предпоследний
определитель
матрицы равен нулю (при
)
Система нейтральна,
если коэффициент
.
Для систем невысокого порядка удобно использовать следующие выражения, полученные на основании критерия Гурвица:
Для системы третьего порядка:
Для системы четвертого порядка:
Критерий позволяет определить граничные значения отдельных параметров в смысле устойчивости. Так для следящей системы третьего порядка, имеющей в разомкнутом состоянии ПФ вида
Получаем характеристический полином замкнутой системы
Допустим, что изменяется параметр «К»
Определим граничное значение коэффициента передачи, заменяя знак неравенства знаком равенства:
Откуда получаем:
Недостатками критерия являются:
- лавинообразное нарастание громоздкости расчетов с ростом порядка уравнения;
-отсутствие гибкости и наглядности при решении задач синтеза системы управления,так как сложно прослеживается связь с параметрами системы;
недостаточность оценки близости к границе устойчивости, определяющей характер и время затухания свободного движения.
Частотный критерий устойчивости Найквиста и его частные случаи
В 1932 году появилась работа американского инженера Найквиста, посвященная исследованию устойчивости операционных ламповых усилителей, где применен рассматриваемый критерий устойчивости.
Достоинства критерия:
- простота и наглядность оценки близости системы к границе устойчивости, связанная с тем, что решение получается на основе анализа частотной характеристики разомкнутой системы;
удобство для синтеза, так как параметры ЧХ разомкнутой системы непосредственно связаны с параметрами динамики элементов системы, что позволяет быстро (при использовании ЛЧХ) оценить их влияние на устойчивость, и спроектировать регулятор, изменяющий эти параметры;
- оценка устойчивости малочувствительна к увеличению порядка уравнения системы.
Практическое применение критерия связывают с характером свободного движения разомкнутой системы (устойчивостью разомкнутой системы). При этом рассматривают три вида такой оценки (три случая):
1. Разомкнутая система устойчива (наиболее часто встречающийся случай);
2.Разомккнтая система нейтральна и нейтрально-устойчива;
3.Разомкнутая система неустойчива.
Первые два случая имеют наибольшее распространение
Оценка устойчивости в последнем случае дает обобщенное решение.
Рассмотрим первый случай применения критерия.
Поскольку разомкнутая система устойчива, то, следовательно, ее ПФ содержит только "левые" полюса. Если знаменатель ПФ разомкнутой системы содержит полином выше второго порядка (случай нулевых полюсов не рассматривается в этом варианте), то необходимо определить корни характеристического уравнения и убедится в том, что они "левые". В большинстве реальных систем этого делать не приходится, так как ПФ прямого тракта контура обычно получается как произведение простейших динамических звеньев не выше второго порядка.
Критерий формулируется в виде:
Если разомкнутая
система устойчива, то для устойчивости
замкнутой системы необходимо и достаточно,
чтобы АФЧХ разомкнутой системы при
изменении частоты от нуля до бесконечности,
не охватывала точку с координатами
(-1,j0
).
Докажем это на примере следящей системы
Пусть ПФ разомкнутой системы имеет вид:
где
полиномы
аргумента «s».
характеристический
полином разомкнутой системы.
Порядок характеристического полинома больше (или равен) порядку полинома числителя (что соответствует условию физически реальной системы).
Передаточная функция замкнутой системы имеет вид:
Рассмотрим
аналитическую функцию
,
у которой в числителе находится
характеристический полином замкнутой
системы, а в знаменателе характеристический
полином разомкнутой системы, имеющие
одинаковый порядок. Определим изменение
аргумента комплексной функции
при изменении частоты от нуля до
бесконечности, приняв исходное условие
критерия – разомкнутая и замкнутая
системы устойчивы. Условие устойчивости
требует, чтобы все корни полиномов
содержали отрицательные действительные
части. В этом случае полный
угол поворота радиуса
– вектора каждого полинома при изменении
частоты от нуля до бесконечности равен
числу корней умноженных на
Так, как полиномы имеют одинаковый
порядок то суммарный угол поворота
радиуса-вектора функции
должен быть равен нулю.
Это возможно, если годограф этой функции
не охватывает начало координат. Если
от рассматриваемой функции перейти к
функции
,
то выполнение полученного условия
соответствует требованию «не охвата»
точки с координатами
.
На Рис. показан вид АФЧХ разомкнутой системы, при котором замкнутая система устойчива.
ЛАЧХ этой системы приведены на Рис. Они показывают, что в такой системе для устойчивости необходимо, чтобы в том диапазоне частот, где ЛАХW лежит выше оси частот, фазовая характеристика не должна располагаться ниже -180 градусов.
Очевидно, граничным условием устойчивости в этом случае будет пересечение ЛАХW оси частот в точке, где ФЧХ пересекает уровень -180 градусов. При этом модуль замкнутой системы равен бесконечности (неограниченный резонансный всплеск), указывающий на появление консервативного звена в ПФ замкнутой системы:
В отношении чувствительности линейной системы к изменению коэффициента передачи разомкнутой системы различают понятия: абсолютно устойчивая система, условно-устойчивая система. Понятие абсолютно устойчивой системы не следует путать с аналогичным названием для оценки устойчивости нелинейной системы при больших начальных отклонениях. Иллюстрация данных понятий приведена на Рис.
Как видно, абсолютно-устойчивая система устойчива при любых отклонениях коэффициента передачи (кроме значения равного бесконечности, при котором она находится на границе устойчивости).
Условно-устойчивая система устойчива только при значениях коэффициента передачи заключенных в некотором диапазоне.