7. Производные высших порядков

Пусть функция имеет производную в каждой точке отрезка [a; b]. Ее производная представляет собой функцию, определенную на отрезке [a; b]. Эта функция тоже может иметь производную на отрезке [a; b] или в некоторых его точках. В этом случае производной второго порядка (второй производной) функции называется производная от производной . Для второй производной функции в точке x применяются обозначения:

Аналогично определяются производные 3-го, 4-го, и т.д. порядков. Производной первого порядка (или первой производной) считается . Для производной n-го порядка будем использовать обозначения

Пример 15. Найти производную указанного порядка.

.

Решение.

Находим первую производную данной функции:

Для нахождения второй производной дифференцируем первую производную:

.

Дифференцируя вторую производную, получим производную третьего порядка:

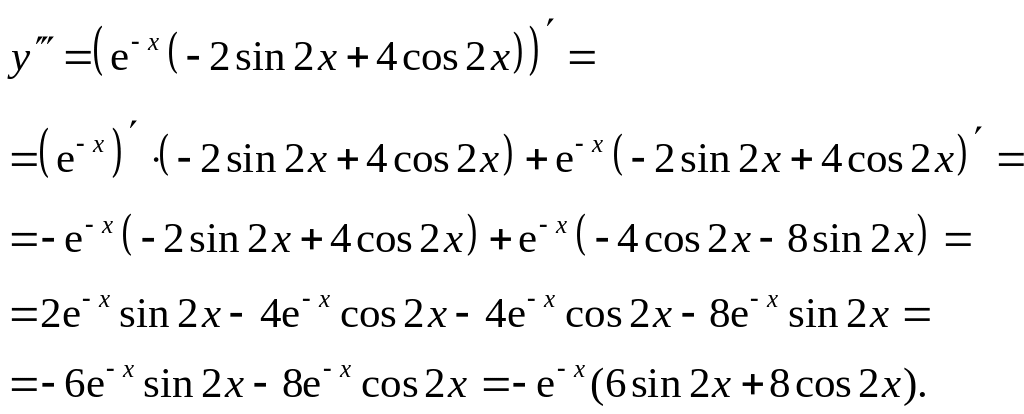
Пример 16. Найти производную -го порядка для функции

Решение.

Будем дифференцировать данную функцию несколько раз, пока не станет ясна формула для производной -го порядка.

Легко увидеть закономерность и записать формулу для производной -го порядка:

8. Производная функции, заданной параметрически

Пусть функции задают параметрически функцию , причем функция φ(t) имеет обратную функцию t=Φ(x). Тогда у = ψ(Φ(х)), и

. (4)

Эта формула дает возможность находить производную функции, заданной параметрически, без определения непосредственной зависимости у от х.

Дифференцируя по х как сложную функцию и используя формулу для производной обратной функции, получим формулу для второй производной функции, заданной параметрически:

. (5)

Пример 17.

Найти и для функции, заданной параметрически:

(– π ⁄ 4 < t < π ⁄ 4).

Решение.

По формуле (5) имеем:

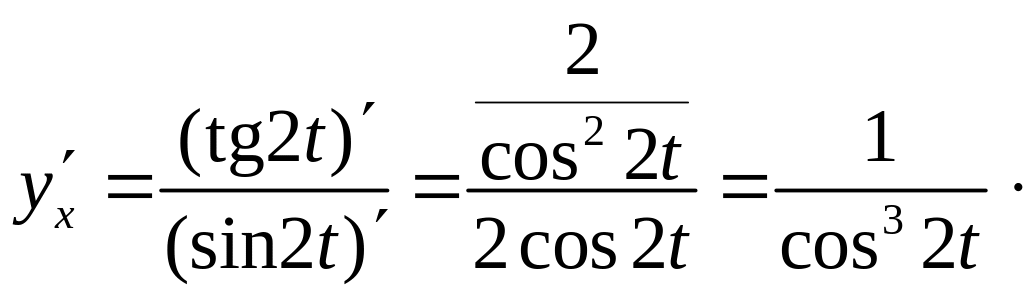
Найдем вторую производную, пользуясь формулой (5):

9. Производная неявной функциИ

Пусть уравнение определяет как неявную функцию от х. для того, чтобы найти необходимо:

1) продифференцировать по х обе части уравнения (при этом y считается функцией от х) и получить уравнение первой степени относительно ;

2) из полученного уравнения выразить .

Продифференцировав по х первую производную, получим вторую производную неявной функции. В выражение для второй производной войдут х, у и . Подставляя в него найденную ранее производную , можно выразить через х и у. Аналогично можно найти и производные высших порядков.

Пример 18.

Найти , если .

Решение.

1) дифференцируем обе части уравнения, учитывая, что y является функцией от х , поэтому , согласно правилу дифференцирования сложной функции. Следовательно получаем:

2) из последнего уравнения находим

Найдем вторую производную .

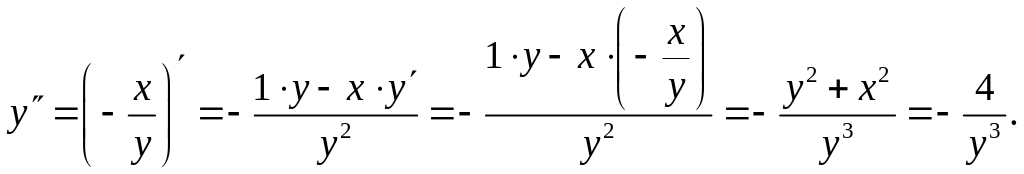
10. Дифференциал

Дифференциалом первого порядка функции y = f(x) называется главная часть ее приращения, линейно зависящая от приращения независимой переменной . Дифференциал dy связан с производной соотношением:

. (6)

Пример 19. Найти дифференциал функции .

Решение.

Находим производную данной функции:

.

Тогда дифференциал функции, в соответствии с формулой (6):

.

С помощью дифференциала можно приближенно вычислить значение функции при малом приращении независимой переменной:

. (7)

Пример 20. Найти приближенно sin 61^o.

Решение.

Полагаем х = 60⁰ = π/3, тогда .

sin 61 ^o .