Справочный материал
1. Производная функции
Пусть функция y =
определена в точке x
и ее окрестности. Пусть аргумент x
получил приращение
.
Тогда функция y =
получит приращение
.
Производной функции в точке x называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.
Таким образом,
. (1)
Производная функции y
=
обозначается как y,
,
или
.
В общем случае для каждого значения х производная имеет определенное значение, т.е. производная является также функцией от х.
Операция нахождения производной функции называется дифференцированием функции.
Если функция y =
имеет производную в точке
,
т.е., если существует
то говорят, что в этой точке функция y = дифференцируема.
Если функция дифференцируема в каждой точке некоторого отрезка [a, b] или интервала (a, b), то говорят, что она дифферцируема на отрезке [a, b] или, соответственно, в интервале (a, b).
Выражения «функция дифференцируема» и «функция имеет производную» означают одно и то же.
2. Таблица производных некоторых функций
В таблице приведены производные основных элементарных функций.
-
1.
(
)2.
3.
4.
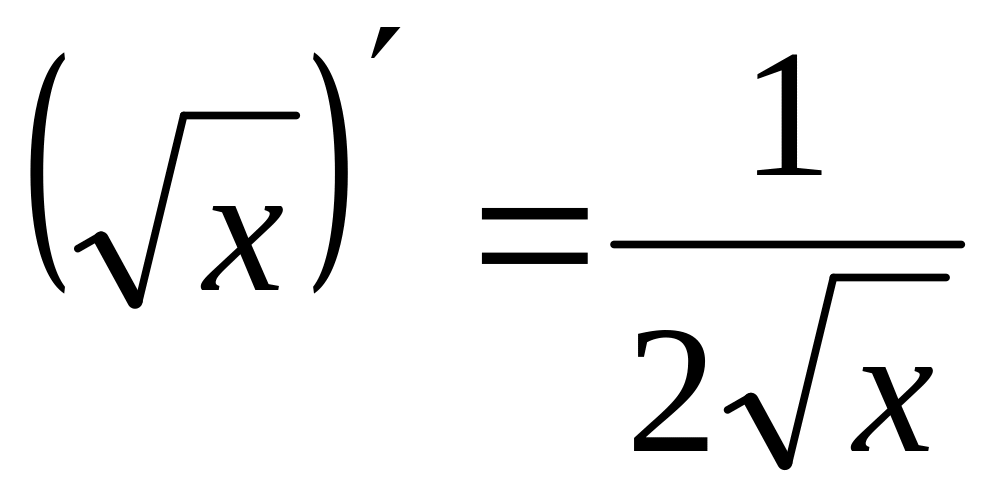
5.
6.
7.
8.
9.
10.
11.
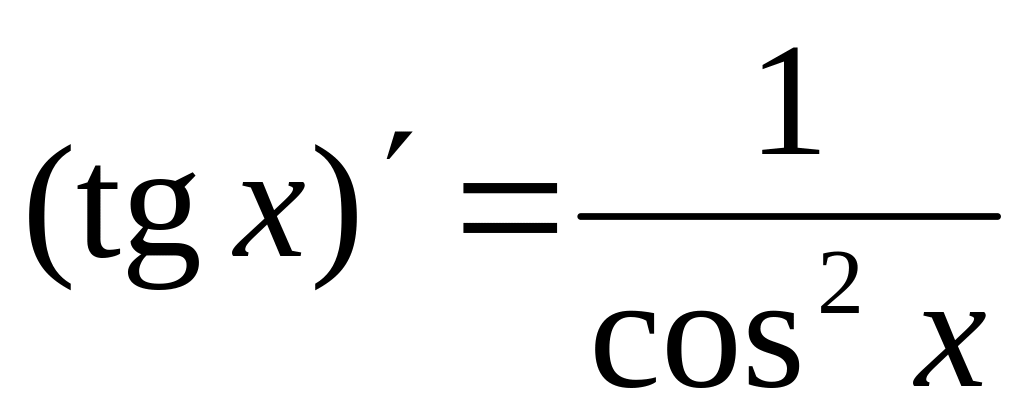
12.
13.
14.
15.
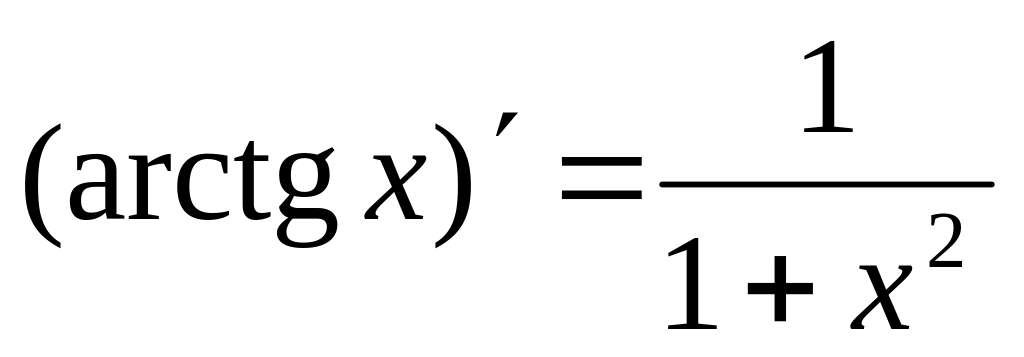
16.
17.
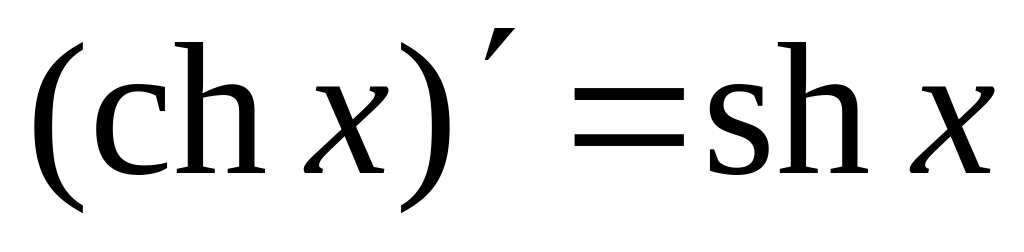
18.
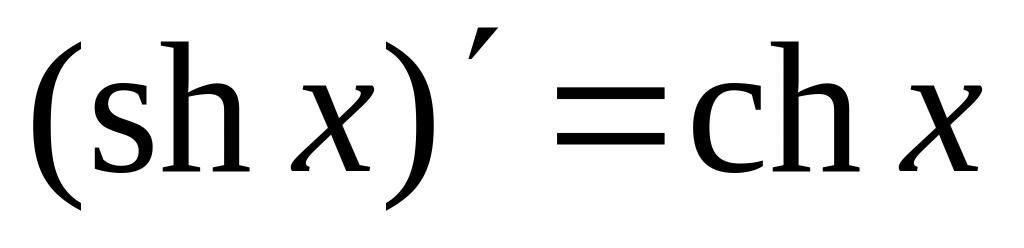
19.
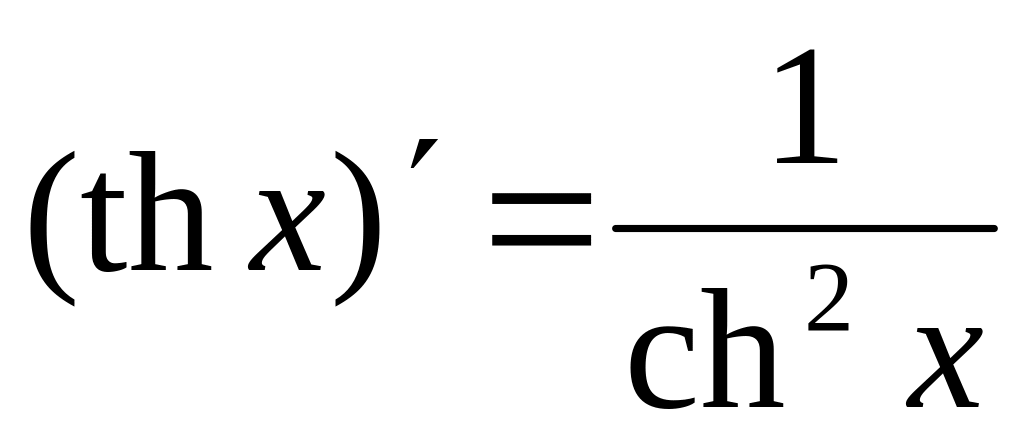
20.
3. Основные правила дифференцирования
Пусть С – постоянная,
и
- дифференцируемые функции.
Правило 1. (С f (x)) = С f (x).
Правило 2.
.
Правило 3.
.
Правило 4.
,
4. Производная сложной функции
Пусть функция u =
(x)
имеет производную в точке x,
а функция
имеет производную в точке u(x).
Тогда сложная функция
имеет производную в точке x,
найти которую можно по формуле
. (2)
Функцию
называют внешней функцией, а функцию
u(x)
– внутренней функцией или промежуточным
аргументом.
Пример 1.
Найти производную функции
.
Решение.
Преобразуем данную функцию к виду
.
Используя правила дифференцирования 1 и 2, а также таблицу производных (пункт 4), получим:
Пример 2.
а) Найти производную функции y
=
.
Решение.
Данная функция является сложной функцией
с промежуточным аргументом
.
Тогда по формуле (2) можем записать:
.
Так как
,
а
,
то окончательно получаем:
Можно обойтись и без подробных записей:
Нижний индекс показывает, по какому аргументу ведется дифференцирование. Далее будет часто использоваться именно такая форма записи.
б) y
= cos(4x +
2) + e9x-1
+ ln 12x+
.
Решение.
Данная функция является суммой функций, поэтому сначала применяем правило 2:
.
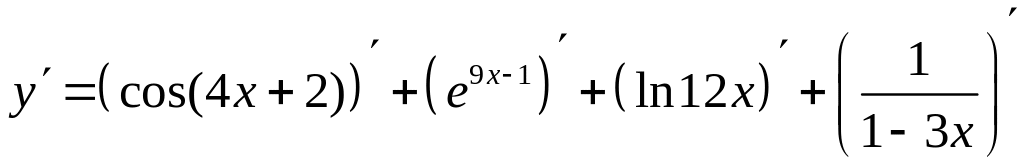Каждое из слагаемых – сложная функция, поэтому для их дифференцирования используем формулу (2).
.
.
Чтобы найти производную
,
запишем функцию в виде:
=
.
Тогда:
Окончательно
получим:
Пример 3.
Найти производную функции y
=
.
Решение.
Преобразуем функцию к виду:
.
Далее воспользуемся правилами дифференцирования 1 и 2:
Функцию
будем рассматривать как сложную функцию
с
промежуточным аргументом
.
По формуле (2):
Функция
представляет собой сложную функцию
с промежуточным аргументом
.
По формуле (2):
Окончательно
получим:
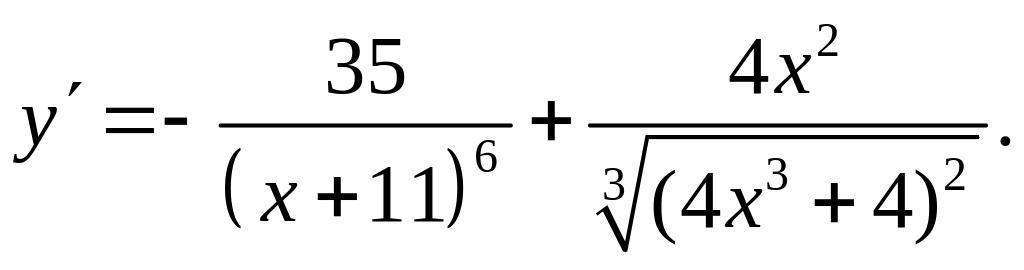
Пример 4.
Найти производную функции
y =
Решение.
Пользуясь правилом 2, запишем:
Каждое из
слагаемых представляет собой сложную
функцию, причем «дважды» сложную. Рассмотрим
подробно первое слагаемое, функцию
.
Она представляет собой сложную степенную
функцию
=(
)3
с промежуточным аргументом
.
По формуле
(2):
.
Но промежуточный аргумент u,
в свою очередь, тоже является
функциейнезависимой переменной х:
.
Поэтому:
.
Окончательно можно записать:
Поизводные остальных слагаемых найдем без подробных пояснений.
Окончательный ответ:
=
+
Пример 5.
Найти производную функции y
= tg6(4x
– 2)·arcsin
.
Решение.
Данная функция представляет собой произведение функций, поэтому для нахождения ее производной воспользуемся правилом 3:
.
Находим производные каждого из множителей, пользуясь формулой (2) для дифференцирования сложных функций.
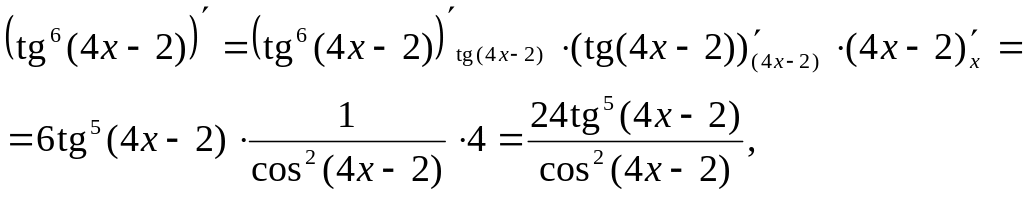
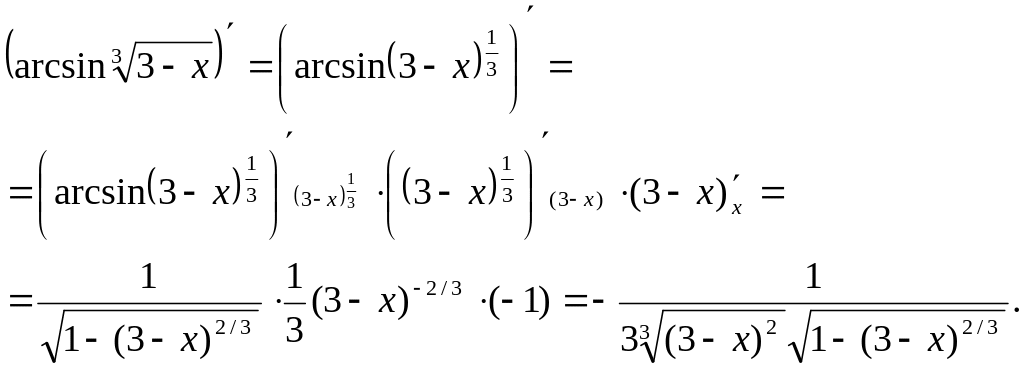
Окончательный ответ:
Пример 6.
Найти производную функции y = ln sin 3x·arccos e3x.
Решение.
Функция является произведением двух функций, поэтому применяем правило 3.
.
Находим производные по формуле (2), т.к. функции являются сложными.
Искомая производная:
Пример 7.
Найти производную функции
.
Решение.
По правилу (4) для дифференцирования частного функций:
Находим производные числителя и знаменателя данной функции:
Окончательный ответ:
Пример 8.
Найти производную функции
Решение.
Функция представляет собой частное функций, поэтому для ее дифференцирования будем пользоваться правилом 4:
.
Поскольку и числитель, и знаменатель являются сложными функциями, то для из дифференцирования необходимо использовать формулу (2):
Окончательно записываем:
Пример 9.
Найти производную функции
.
Решение.
По правилу (4) для дифференцирования частного функций:
,
.
Окончательно получим:
Пример 10.
Найти производную функции
.
Решение.
Применяем правило 4:
Числитель представляет собой произведение двух сложных функций, поэтому для нахождения производной числителя используем правило 3 и формулу (2):
Знаменатель также сложная функция, для нахождения производной снова применяем формулу (2):
Окончательно получим:
=
Пример
11.
.
Решение.
Преобразуем данную функцию к виду:
.
Функция является сложной: внешняя функция - степенная, внутренняя – частное двух линейных функций. Для нахождения производной будем пользоваться формулой (2) и правилом дифференцирования 3:
