IV. Булевы функции.

8. Алгебра Жигалкина. Полином Жигалкина. Теорема о полиноме Жигалкина.

Алгебра Жигалкина.

Опр. Алгебра ‹P₂;&; Å› над множеством булевых функций с двумя бинарными операциями & и Å называется алгеброй Жигалкина.

В алгебре Жигалкина выполняются следующие соотношения:

x Å y = y Å x x(yÅz) = xy Å xz

x Å x = 0 x Å 0 = x

а так же соотношения булевой алгебры, относящиеся к конъюнкции и константам.

П олином Жигалкина.

Опр. Формула вида где множество {i₁, ..., i_s} пробегает все возможные подмножества множества {1, ..., n} и a_i1..._is называется полиномом Жигалкина.

О т булевой формулы всегда можно перейти к формуле алгебры Жегалкина и, следовательно, полиному Жегалкина, используя равенства:

Теорема о полиноме Жигалкина.

Теорема. Каждая функция из P₂ может быть выражена при помощи полинома Жигалкина причем единственным образом.

Док-во. В силу полноты системы {1,&,Å} каждая функция из P₂ может быть выражена в виде полинома Жигалкина.

Единственность: покажем, что между множеством всех функций от n переменных и множеством всех полиномов Жигалкина от n переменных существует взаимно однозначное соответствие.

Число полиномов Жигалкина от n переменных x₁,...,x_n. Число различных слагаемых (конъюнкций переменных) в полиноме равно числу различных подмножеств множества из n элементов, т.е. 2ⁿ.

Ч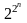 исло различных полиномов, которые можно образовать из этих конъюнкций, равно числу всех подмножеств множества конъюнкций, т.е. .

Таким образом, число всех полиномов Жегалкина от n переменных равно числу всех функций от n переменных.

Так как разным функциям соответствуют разные полиномы (одна и та же формула не может представлять две разные функции), то тем самым между множествами функций и полиномов установлено взаимно однозначное соответствие, что и доказывает единственность полинома для каждой функции.

V. Кодирование

3. Свойство префиксности схемы кодирования . Взаимно однозначное кодирование. Теорема – условие однозначности декодирования.

Префикс слова.

Для непосредственной проверки взаимной однозначности необходимо просмотреть бесконечное число слов.

Простым достаточным признаком, позволяющим по схеме алфавитного кодирования определить, обладает ли алфавитное кодирование свойством взаимной однозначности, является условие префиксности

Опр. Пусть слово β имеет вид β = β’ β ”. Тогда β’ называется началом или префиксом слова β, а β” – окончанием слова β.

Пустое слово ᴧ и само слово β считаются началами и окончаниями слова β.

Условие префикса.

Опр. Схема ∑ обладает свойством префикса, если для любых i и j, i≠j элементарный код β_i не является префиксом элементарного кода β_j:

∀ i ≠ j β_i, β_j ∈ B^* ∀β’ ∈ B^* β_j ≠ β_i β’

Взаимно однозначное кодирование.

Пусть S=A*, т.е. источник сообщения порождает множество всех слов в алфавите A.

Если отображение множества A* на множество всех кодов F_∑ A*, индуцируемое схемой ∑, взаимно однозначно, то кодирование допускает однозначное декодирование. В этом случае говорят так же, что алфавитное кодирование является взаимно однозначным.