I. Множества

2. Конечные и бесконечные множества. Сравнимые множества. Мощность множества. Булеан.

Конечные и бесконечные множества.

Опр. Множество считается конечным, если имеет конечное количество элементов.

Опр. Множество считается бесконечным, если имеет бесконечное количество элементов. (множество точек отрезка прямой)

Опр. Пустое множество - это множество не содержащее ни одного элемента

Сравнение множеств.

Опр. Множество A является подмножеством множества B, если каждый элемент A является элементом B

A Í B Û ("xÎA) [xÎA ®xÎ B]

Если A Í B и xÏB, то xÏA

Опр. Множество A является собственным подмножеством множества B, если A Í B и A¹ B.

A Ì B Û ($xÎ B)[xÏA]

Опр. Если A Í B (A Ì B ), то множества A и B называют сравнимыми.

A Í A для всякого множества A

Ø Í A для всякого множества A

Если A Í B и B Í C, то A Í С

A Ë B Û ($xÎ A)[xÏB]

Булеан.

Опр. Булеаном (обозначается 2^А) называется семейство всех подмножеств данного множества А.

2^А={B: B Í A }

Пример 1.

Дано множество А={1,2,3}.

Записать все подмножества данного множества.

Решение

2^А={{1},{2},{3},{1,2},{1,3},{2,3},{1,2,3},{Ø}}.

Мощность множества.

Опр. Мощностью конечного множества A (обозначается ½A½) называют число его элементов

½Ø½=0, ½{Ø}½=1, ½{x}½=1, ½{1,{1,2}½=2,

½{{1,2,3,},Ø}½=2, ½{1,2,1,3}½=3

Утверждение. Если ½A½=n, то ½2^А½=2ⁿ

II. Отношения

4. Представление отношений. Теорема и представлении отношений в ЭВМ.

Представление отношений.

Способы задания отношений:

1) Перечислением всех наборов в отношении R={(a,b), (c,d), …}.

Данный способ задания обычно используется , когда R задано на конечных множествах с небольшим числом элементов.

Пример:

Пусть множества имеют вид: М₁={4,5}, М₂={x,y}.

В качестве отношения R

можно рассмотреть подмножество R={(4,x), (5,y)}.

2) Общим свойством или предикатом.

Существуют две формы задания

1. R={(a₁,…,a_n) │ P(a₁,…,a_n)}

2. (a₁,…,a_n)  R <=> P(a₁,…,a_n),

где P(a₁,…,a_n) - предикат

Пример:

Отношение из предыдущего примера М₁={4,5}, М₂={x,y}, R={(4,y), (5,y)}

Можно задать двумя способами:

R={(a,b) │ a-любое & b=y)}

3) Орграфом (ориентированным графом), диаграммой на плоскости.

4) Матрицей отношений.

Бинарному отношению RM², соответствует квадратная матрица n –го порядка, в которой элемент C_ij , стоящий на пересечении i–й строки и j–го столбца, равен 1, если имеет место a_iRa_j, и 0 в противном случае.

II. Отношения

10. Функции. Инъекция, сюрьекция, биекция. Теорема о тотальной биекции.

Функции и их свойства.

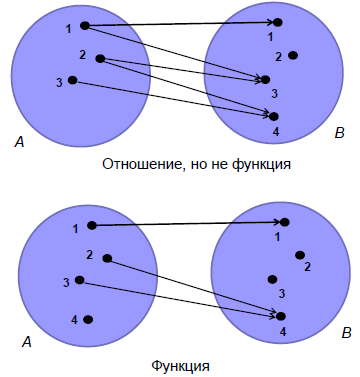
Опр. Пусть f – отношение из A в B.

Свойство однозначности: (a,b)  а & (a,c)  а -> b=c

Само отношение называется функциональным или функцией и обозначается:

f: A->B или

Если f: A->B, то используется префиксная форма записи:

b = f(a) := (a,b)  f

a - аргумент, b - значение.

fA={aA: ƎbB & b=f(a)} – область определения функции

fB={bB: ƎaA & b=f(a)} – область значений функции

Если fA=A, то f называется тотальной

Если fA≠A, то f называется частичной

Опр. Сужением функции f:A->B на множество M A называется функция

f_M={(a,b): (a,b)f & aM}

Опр. Функция f: A1×A2 × … ×A_n->B называется функцией от n аргументов или

n –местной: b=f(a₁ ,a₂,…,a_n)

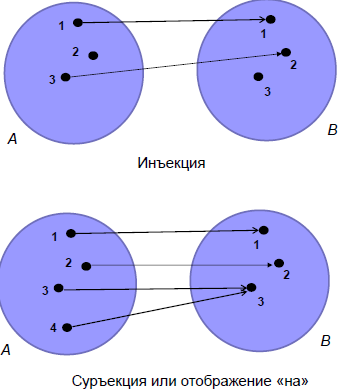
Опр. Пусть f : A->B. Функция f называется

- инъективной, если b=f(a₁) и b=f(a₂) a₁=a₂.

- сюръективной, если ( b B)( ƎaA) [b=f(a)].

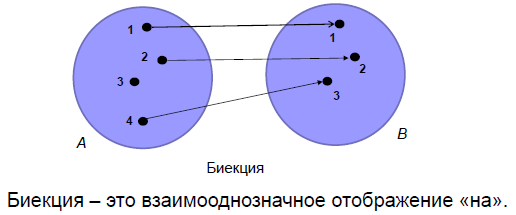
- биективной, если она инъективна и сюръективна.

Биекция – это взаимооднозначное отображение «на».

Теорема.

Если f : A->B – тотальная (f_A=A), то отношение f ^-1 B×A является биекцией.

Док-во. Т.к. f - биекция, то

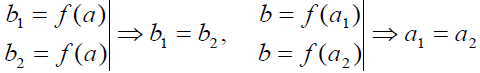
( bB)(ƎaA) [b=f(a)].

Покажем, что

f ^-1:={(b,a): aA, bB, b=f(a)}- функция

Пусть

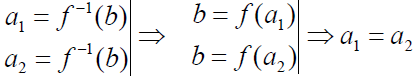
Следовательно, f ^-1 – функция.

Покажем, что f ^-1 – инъекция.

Пусть

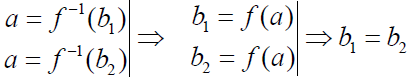
Покажем, что f ^-1 – сюръекция. От прот.

Пусть (ƎaA)(-ƎbB)[a = f^-1(b)]

Тогда (ƎaA)( bB)[a ≠ f^-1(b)]

Имеем:

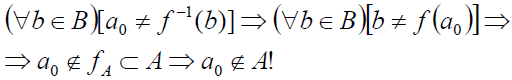
Т .о., f ^-1 – функция, инъективная и сюръективная f ^-1 – биекция