
- •Векторлар . Векторларды қосу амалы және оның қасиеттері (дәлелдеуімен)
- •2.Векторларды санға көбейту амалы және оның қасиеттері (дәлелдеуімен)
- •3. Сызықтық тәуелді векторлар жүйесі. Сызықтық тәуелді векторлар жүйесінің қасиеттері. (дәлелдеумен)
- •6. Компланар векторлардың анықтамасы. Үш вектордың компланар болу белгісі. (дәлелдеумен)
- •7.Вектордың скаляр проекциясы және оның қасиеттері. (дәлелдеумен)
- •8. Вектордың векторлық проекциясы және оның қаситеттері.
- •9. Екі вектордың скаляр көбейтіндісі және оның қасиеттері
- •12. Векторлардың аралас көбейтіндісі және оның геометриялық мағынасы. Векторлардың аралас көбейтіндінің есептеу формуласы. (дәлелдеумен)
- •13. Жазықтықтағы түзулердің параметрлік, канондік теңдеулерін қорытып шығару. Жазықтықтағы түзудің жалпы теңдеуі.
- •Жазықтықтағы екі түзудің өзара орналасуы және жазықтықтағы екі түзудің арасындағы бұрыш. (дәлелдеумен)
- •15. Жазықтықтағы түзудің нормал теңдеуін қорытып шығару.
- •17. Жазықтықтың теңдеулерілерін қорытып шығару.
- •19. Екі жазықтықтың өзара орналасуы. (дәлелдеумен)
- •20. Екі жазықтықтың арасындағы бұрыш.
- •22.Кеңістіктегі нүктеден жазықтыққа дейінгі арақашықтықтың формуласын қорытып шығару.
- •24. Кеңістіктегі түзумен жазықтықтың өзара орналасуын зерттеу.
- •25. Кеңістіктегі түзумен жазықтықтың арасындағы бұрыш.
- •26. Эллипс. Канондық теңдеу
- •29. Матрицаларды санға көбейту амалы және оның қасиеттері. (дәлелдеумен)
- •33. Матрицаны сатылы түрге келтіру Гаусс алгоритмі.
- •38. Матрицаның рангі туралы теорема және оның салдары.
- •39. Ауыстыру туралы лемма.
- •40.Сызықтық алгебралық теңдеулер жүйесі және оның түрлері.
- •41. Матрицаны сатылы түрге келтіру Гаусс алгоритмі.
- •43. Крамерлі жүйелер. Сатж-ны шешудің Крамер әдісі.
- •44. Кері матрицаның анықтамасы. Кері матрицаны табудың Гаусс-Жордан алгоритмі.
- •46. Қойылымдар. Екі қойылымның көбейтіндісі.
- •47. Анықтауыштың негізгі қасиеттері. (дәлелдеумен)
- •50. Сызықтық кеңістіктің анықтамасы. Мысалдар. Сызықтық кеңістіктердің базисы және өлшемі. Сызықтық кеңістіктердің өлшемі туралы теорема.
38. Матрицаның рангі туралы теорема және оның салдары.
Теорема. Кез келген мат-н ың жолдар рангі бағандар рангіне тең.
Салдар. Кез келген Аматрицасы үшін r (A)=r(A').
Теорема. Екі матрицаның көбейтіндінің рангі көбейткіштердің рангтерінен аспайды.Матрицаны керіленетін матрицаға көбейткенде оның рангі өзгермейді.
Салдар1. Элементар түрлендірулер матрицаның рангтерін өзгертпейді.
Салдар2. (P) матрицасы керіленетін матрица болуы үшін r (A)= п болуы қажетті және жеткілікті.
А мат-ның рангін табу үшін оны сатылы түрге келтіреміз(сатылы түріне жол н/е баған бойынша келтіреміз).Оны S деп белгілейміз.S сатылы түрдегі мат-ғы нөлдік емес жолдардың саны А мат-ның рангі болады.
( ,
,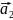 ,…,
,…, )
век-лар жүйесі бер/сін.Осы вектор
жүйесінен матрица аламыз.Егер А мат-ның
сатылы түрінде соңғы жолы нөлдік болса,
онда (
,
,…,
)
век-лар жүйесі сыз-тық тәуелді.Егер А
мат-ның сатылы түрінде соңғы жолы нөлдік
емес болса, онда (
,
,…,
)
век-лар жүйесі сыз-тық тәуелсіз.
)
век-лар жүйесі бер/сін.Осы вектор
жүйесінен матрица аламыз.Егер А мат-ның
сатылы түрінде соңғы жолы нөлдік болса,
онда (
,
,…,
)
век-лар жүйесі сыз-тық тәуелді.Егер А
мат-ның сатылы түрінде соңғы жолы нөлдік
емес болса, онда (
,
,…,
)
век-лар жүйесі сыз-тық тәуелсіз.
39. Ауыстыру туралы лемма.
Тұжырым: векторлар жүйесінің бірінші векторы
нөлден өзгеше болсын, яғни с1
векторлар жүйесінің бірінші векторы
нөлден өзгеше болсын, яғни с1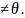 онда
онда
 жүйесі
сызықтық тәуелді болуы үшін кем дегенде
бір сί
векторы оның алдындағы
жүйесі
сызықтық тәуелді болуы үшін кем дегенде
бір сί
векторы оның алдындағы
 векторлары
арқылы сызықтық өрнектелуі қажетті
және жеткілікті.
векторлары
арқылы сызықтық өрнектелуі қажетті
және жеткілікті.
Салдар:
векторлар
жүйесі сызықтық тәуелсіз, ал
 сызықтық
тәуелді болса, онда сί
векторы
векторлары
арқылы сызықтық өрнектеледі.
сызықтық
тәуелді болса, онда сί
векторы
векторлары
арқылы сызықтық өрнектеледі.
Теорема:
егер
 мен
мен
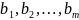 векторлар жүйелері үшін келесі екі шарт
орындалса: 1)
жүйесі сызықтық тәуелсіз; 2)
векторлары
векторлар жүйесі арқылы сызықтық
өрнектеледі, онда
векторлар жүйелері үшін келесі екі шарт
орындалса: 1)
жүйесі сызықтық тәуелсіз; 2)
векторлары
векторлар жүйесі арқылы сызықтық
өрнектеледі, онда
 теңсіздігі орындалады. Дәләлдеу: қосымша
теңсіздігі орындалады. Дәләлдеу: қосымша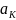 ,
векторлар жүйесін қарастырсақ.
,
векторлар жүйесін қарастырсақ.
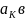 екторы
осы жүйенің қалған
векторлары арқылы теореманың 2-шарты
бойынша сызықтық өонектеледі. Демек,
бұл жүйе сыз-қ тәуелді болады. Тұжырым
бой-ша ,осы жүйенің бір bί
векторы оның алдынғы
екторы
осы жүйенің қалған
векторлары арқылы теореманың 2-шарты
бойынша сызықтық өонектеледі. Демек,
бұл жүйе сыз-қ тәуелді болады. Тұжырым
бой-ша ,осы жүйенің бір bί
векторы оның алдынғы
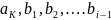 векторлары арқылы сызықтық өрнектеледі.
Енді
векторлары арқылы сызықтық өрнектеледі.
Енді
ж/е векторлар
жүйелерітеореманың 2 шартынқанағаттандырады..
векторлар
жүйелерітеореманың 2 шартынқанағаттандырады..
Шарт 1) жүйесі үшін орындалуы сыз-қ тәуелділіктің 4-ші қасиеті (сыз-қ тәуелсізжүйеденбірнешевекторлардыалсақ, қалғанвекторлар да сыз-қ тәуелсіз жүйені құрайды.) 2-шарттың орындалуын векторы үшін тексеретін болсам, теореманыңбастапқы 2-шарты бой-ша векторын векторлары арқылы жіктепалып , солжіктеуіндеbίвекторын оның
векторларыарқылыжасалғансыз-қ
өрнегіменауыстырсақ, онда векторлары ар-ы өрнектелуін
табамыз.
векторлары ар-ы өрнектелуін
табамыз. векторларының
векторларының
векторлары арқылы сыз-қ өрнектелуі дәл осылай дәләлденді.
Салдар.Егер
тәуелсіз
мен
жүйелерінің барлық векторлары басқа
жүйе арқылы жіктелетін болса, онда

Дәлелдеу:
теорема бой-ша
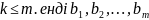 жүйесін
бірінші, ал
жүйесін екінші деп қарастырсақ, онда
теоремадан
жүйесін
бірінші, ал
жүйесін екінші деп қарастырсақ, онда
теоремадан

40.Сызықтық алгебралық теңдеулер жүйесі және оның түрлері.
α 1 x1+ α 2x2 +…+α nxn=β (1) теңдіктіx1, x2 ... xnбелгісіздіктері бар сызықтық алгебралық теңдеу деп атайды.
Бұл
жерде
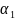 ,
, ,
,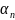 -
сызықтық теңдеудің коэффициенттері
деп аталады және олар нақты немесе
комплекс сандар. Β саны-сызықтық теңдеудің
бос мүшесі деп аталады және ол да нақты
немесе комплекс сан. (1)теңдеуде
коэффициенттердің жоқ дегенде біреуі
0
-
сызықтық теңдеудің коэффициенттері
деп аталады және олар нақты немесе
комплекс сандар. Β саны-сызықтық теңдеудің
бос мүшесі деп аталады және ол да нақты
немесе комплекс сан. (1)теңдеуде
коэффициенттердің жоқ дегенде біреуі
0 болсын.
болсын.
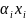 =β-
=β- -
- -…-
-…-
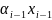 -
- -…αnxn
-…αnxn
 =
= -…-
-…-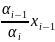 - …-
- …- xn(2)
xn(2)
Екінші өрнекті бірінші теңдеудің жалпы шешімі деп атайды. Бұл жерде –базистік белгісіз, ал қалған белгісіздер-еркін белгісіздер.
Анықтама1.САТЖ анықталған деп аталады,егер де оның жалғыз шешімі бар болса.
Анықтама2.САТЖ үйлесімді деп аталады, егер оның жоқ дегенде бір шешімі бар болса.
Анықтама3.САТЖ анықталмаған деп аталады, егер де оның ақырсыз көп шешімі болса.
Анықтама4.САТЖ үйлесімсіз деп аталады, егер оның бір де бір шешімі жоқ болса.
САТЖ-ның шешімдер жиыны осы САТЖ-дағы барлық теңдеулердің шешімдер жиындарының қиылысуы болады.
