12. Векторлардың аралас көбейтіндісі және оның геометриялық мағынасы. Векторлардың аралас көбейтіндінің есептеу формуласы. (дәлелдеумен)

Үш вектордың аралас көбейтіндісі.Анықтама.Ретке келтірілген нөлдік емес a,b,c векторлары үштігінің аралас көбейтіндісі деп a*b векторымен c векторының скалярлық көбейтіндісіне тең санды айтады. Үш вектордың аралас көбейтіндісі a*b*c деп белгіленеді. Сонда, анықтама бойынша,а*b*c =(a*b)*c .

Егер a,b,с векторларының кем дегенде біреуі нөлдік вектор болса,онда аралас көбейтінді нөлге тең деп саналады.

Геометриялық мағынасы. 1-теорема. Компланар емес a,b,c векторларының көбейтіндісі ортақ бас нүктеден шыққан a,b,c векторларына салынған, егер a,b,c векторлар үштігі оң жақты болса,онда оң таңбамен,ал a,b,c үштігі сол жақты болса,теріс таңбамен алынған параллелепипедтің көлеміне тең болады. A,b,c векторлары компланар емес деп санап, мына екі жағдайды қарастырамыз. Алдымен, a,b,c үштігі оң жақты деп санайық.

А=OA, b=OB, c=OC векторларына салынған параллелепипедтің көлемін V арқылы белгілейік. Сонда V=S*h.

Мұндағы S a және b векторларына салынған параллелограмның ауданы,ал h=\OD\-параллепипедтің биіктігі. A*b=d деп белгілейік. Екі вектордың векторлық көбейтіндісінің анықтамасы бойынша;1\ \d\=s;

2\d векторы а және b векторлары жүргізілген жазықтығына перпендикуляр;

3\a,b,d векторлар үштігі оң жақты болады. Бұдан с және d векторлары жазықтығының бір жағында оорналасқандығы шығады,демек

OCD үшбұрышынан h=\c\*cosµ \1\

Енді d және с векторларының скаляр көбейтіндісін қарастырайық. Сонда ол бір жағынан d*c=(a*b)*c \2\

болса, ал екінші жағынан ,|d|=s теңдігі мен формуланы пайдалансақ,онда

d*c=|d|*|c|*cosµ=S*h=V \3\

болады,\2\ және\3\-формулалардың оң жақтарын теңестірсек,(a*b)*c=V болады.

Енді a,b,c векторлар үштігі сол жақты деп санайық. Сонда a*b=d және с векторлары α жазықтығының әртүрлі жағында жатады,демек,(c^,d)=µ>∏/2, яғни,соsµ< 0. OCD үшбұрышынан мына теңдік шығады. h=|c|*cosµ=|c|*cos(∏-µ)=-|c|*cosµ \4\

Егер |d|=S және \4\ формулаларын ескерсек,онда d*c=|d|*|c|*cosµ=S*(-h)=-S*h=-V \5\

Ал,егер a,b,c векторлар үштігі сол жақты болса, онда \2\ және \5\ формулалардан мына формуланы шығарып аламыз. (a*b)*c=-V. Сонымен, кез келген компланар емес a,b,c векторлар үштігі үшін V=|(a*b)c| формуласын аламыз.

Есептеy формаласы:

ТКЖ:a=(a₁,a₂,a₃), b( b₁,b₂,b₃)

i, j,k-орта нормаланған базис

[a,b]=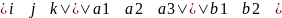 =i*| -j +K

[a,b]=(a₂b₃-b₂a₃-a₁b₃+b1a3*a1b2-b1a2) S=

C=(c1,c2,c3) a=(a1,a2,a3) b=(b1,b2,b3)

(a, b ,c)=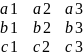

13. Жазықтықтағы түзулердің параметрлік, канондік теңдеулерін қорытып шығару. Жазықтықтағы түзудің жалпы теңдеуі.

Мына есепті шығарайық:бағыттаушы векторы =(l,m)–ке тең,берілгенM˳(x˳,y˳) нүктесін басып өтетін d түзуінің теңдеуін табыңдар.M(x,y) d нүкте болсын,сонда =(x-x˳,y-y˳). Cондықтан || /1/,бұдан = 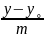- (канондық теңдеу), яғни кез-келген нүктесінің M(x,y) координаталары /1/- теңдеуді қанағаттандырады.

Керісінше ,M*(x*,y*) нүктесі,координаталары \1\ теңдеуді қанағаттандыратын нүкте болсын,яғни = . Олай болса,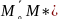 =(x*-x˳,y*-y˳)және =(l,m) векторлары коллинеар болады,демекM*(x*,y*) . Сөйтіп /1/ -теңдеу іздеген теңдеуіміз болып шықты. Бұл теңдеу түзудің канондық теңдеуі деп аталады. /2/-формуладағы бөлшектердің біреуінің бөлімі нөлге айналуы мүмкін. /әрине 0 болғандықтан екі бөлшектердің бөлімдері бір уақытта нөлге тең болмайды. Бұл жағдайда, 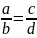пропорциясын ad=bc теңдігінің орындалуын пара-пар деп түсінгендіктен,ол бөлшектің сәйкес алымын нөлге тнң деп санаймыз.

/1/теңдеудегі теңдіктің оң және сол жағындағы бқлшектердің жалпы мәнін t деп белгілейік. Сонда t парметрінің өзгеру облысының барлық сан осі (R) болатынына көз жеткізу қиын емес.

Шынында да,бөлшектердің кемінде біреуіңің бөлімі нөлге тең емес,демек,бөлшектің сәйкес алымы кез-келген мәнді хабарлай алады. Олай болса t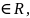 яғни - Сонымен /1/-теңдеуден немесе теңдеулерін аламыз.

x-x˳=lt , y-y˳=mt немесе \2\

/2/-теңдеулер түзудің парметрлік теңдеулері деп аталады.

Анықтама(Жазықтықтағы түзудің жалпы теңдеуі.).Ax+By+C=0 \1\ теңдеу түзудің жалпы теңдеуі деп аталады.

1-теорема.Жалпы теңдеуі арқылы анықталған түзуі,сол түзудің нормалдық векторы деп аталатын n=(A,B) векторына перпендикуляр болады.\1\ теңдеу кем дегенде бір (x˳,y˳) шешімі бар болатынын тексеру қиын емес.Шынында да,A және B коэффициенттері бір уақытта нөлге айналмайтын болғандықтан,A≠0 деп алайық.Егер y=y˳ десек,онда \1\ теңдеуден мына мәнді шығарамыз: x˳=-(B/A)y˳-(C/A).Демек,Ax˳+By˳+C=0 \2\

теңбе-теңдігі орындалатындай M˳(x˳y˳) нүктесі табылады.Егер \1\ теңдеуден \2\ теңбе-теңдігін мүшелеп алып тастасақ,онда \1\ теңдеуге мәндес мына теңдеуді аламыз:A(x-x˳)+B(y-y˳)=0 \3\.

\3\ шарт d түзуінде жатқан кез келген M˳M=(x-x˳,y-y˳)векторы мен n=(A,B) векторының перпендикулярлық (ортоганалдық) шартын (белгісін) көрсетеді.

2-анықтама./3/-теңдеу M˳(x˳,y˳) нүктесі арқылы өтетін. =(a,b) векторына перпендикуляр түзу теңдеуі деп аталады.

2-теорема. Нөлдік емес =(l,m) векторы /1/-жалпы теңдеумен берілген d түзуінің бағыттаушы векторы үшін Al+bm=0 \4\ шартының орындалуы қажетті және жеткілікті.

Қажеттілік. =(l,m) 0 векторы

Ax+by+c=0, +

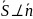tеңдеуімен анықталған d түзуінің бағыттаушы векторы дейік. 1-теорема негізінде =(A,B) болады. Бұдан. демек,бұл екі вектордың скалярлық көбейтіндісі нөлге тең,яғни * =A*l+ B*m=0. Қысқаша: s векторы d түзуінің бағыттаушы векторы болғандықтан, * =A*l+ B*m=0

Жеткіліктілік. Al+bm=0 болсын. Сонда 0= Al+bm= * ↔ ||d

Яғни,анықтама бойынша s векторы d түзуінің бағыттаушы векторы болады.

Салдар. =(-B,A)векторы жалпы теңдеуімен анықталған d түзуінің бағыттаушы векторы болады. Шынында да, S=(-B,A) векторы үшін /4/-шарт орындалады.