1. Векторлар . Векторларды қосу амалы және оның қасиеттері (дәлелдеуімен)

Егер кесіндінің ұзындығымен қоса бағытыда берілген болса,онда оны вектор деп атайды. Егер 2 век-дың ұзындығымен қоса бағыттас болса,олар тең.

Егер О (·)-сі А және В (·) арасында орналасса ,онда а және в қарама –қарсы бағытталған д/а.(а↑↓в)

Егер О (·) А және В (·)арасыда орналасса ,онда а және в бағыттас.(а↑↑в)

.Екі вектордың қосындысы a + b

векторы деп, b векторының басы a векторының ұшымен түйістірілген

жағдайда, басы a векторының басымен, ұшы b векторыныңұшымен сəйкес келетін векторды айтамыз. Анықтамаға сəйкес a жəне b

қосылғыштары мен олардың

қосындысы a + b үшбұрыш құрады. Сондықтан еківекторды қосу ережесі“үшбұрыш ережесі ” депаталады.Векторларды қосу амалы келесі қасиеттерге ие:

1. А) a + b = b + a (коммутативтілік);

б) (паралелограм) а+в =АВ +BC = АС в+а = АD+DС = АС

2) (a + b ) + c = a + (b + c ) (ассоциативтілік);

а+в=ОА +АВ=ОВ

ОВ+с=ОВ+ВС=ОС

в+с=АВ+ВС=АС

а+АС=ОА+АС=ОС

3) Кез келген a векторы үшін

a + θ=θ+а= a(нөлдік векторқасиеті);

бас нүктесімен ұшы беттесетін бектор нөлдік.бағыты анықталмаған,ұзындығы -0

а= АВ; ВВ=θ ; АВ+ВВ =АВ, а+θ=а;

АА=θ; АА+АВ=АВ; θ+а=а

4) а+в=в+а=θ

АВ+ВА=АА=θ

ВА+АВ=ВВ=θ в=-а

Кез келген a векторына a+ a₁= 0 болатындай, қарама -қарсы вектор a₁ табылады ( a₁ векторын алу ұшын a

векторыының басы мен ауыстыру жеткілікті)a векторына қарама - қарсы векторды (−a) арқылыбелгілейміз.

2.Векторларды санға көбейту амалы және оның қасиеттері (дәлелдеуімен)

а векторының λнақты санына көбейтіндісі λ>0 жағдайда ↑↑ aλ бағыттас, λ<0 жағдайда aλ↑↓бағытталған және ұзындыығы | λ |*|а| тең веторды айтамыз.

Векторды санға көбейту амалы келесі қасиеттерге ие:

1) λ(μa) = (λμ)a (көбейткіштердің ассоциативтілік қасиеті);

2) λ(a+b)=a λ+ bλ

(λ+μ) a = aλ+aμ

( дистрибутивтілік қасиет).

3)1*а=а

4) (α*β) = α*(β

3. Сызықтық тәуелді векторлар жүйесі. Сызықтық тәуелді векторлар жүйесінің қасиеттері. (дәлелдеумен)

Егер Ө-ны а₁,а₂,…a_n векторлары арқылы ең болмағанда коэффициеттерінің біреуі нөлден өзгеше болатындай етіп сызықтық өрнектеледі :Ө=α ₁a+ α ₂a₂+… α_na_n, онда а₁,а₂….а_n векторлар жүйесі сызықтық тәуелді деп аталады:Қасиеттері:1 егер а₁,а₂….a_n векторлар-ң ең болмағанда біреуі нөлдік вектор болса,онда жүйе сызықтық тәуелді болады,Дәлелдеу:Анықтық үшін а_n=Ө болсын,онда 0*а₁+0*а₂+….+0*a_n-1+1*a_n=Ө, демек а₁,а₂,….а_n сызықтық тәуелді жүйе,2қасиет жалғыз вектордан тұратын жүйе сызықтық тәуелді болуы, үшін бұл вектордың нөлдік вектор болуы қажетті және жеткілікті дәлелдеу:егер жалғыз а₁ векторы нөлдік вектор болса ,онда бұл жүйе қасиет 1 бойынша сызықтық тәуелді ;3)егер сызықтық тәуелді жүйеге бірнеше вектор қоссақ,онда жаңа жүйе де сызықтық тәуелді болады, дәлелдеу а₁,а₂,….a_k векторлар жүйесі сызықтық тәуелді болсын,а-а бойынша α₁, α₂…. Α_k нақты сандарды табылып:α₁a₁+ α₁a₁+….. α_k a_k=Ө,ал α _1, α_2,,,,,α_к сандары арасында ең болмағанда біреуі нөлден өзгеше,берілген жүйеге қосымша кез келген а_к+1,а_к+2,……,a_n векторларын қарастырайық,онда α₁a₁+….. α _k a_k+0a_k+1+…..0a_n=Ө,демек а₁,а₂,….a_n векторлар жүйесі де сызықтық тәуелді;4)a₁,a₂,….a_n(2≤n)векторлар жүйесінің ,сызықтық тәуелді болуы үшін осы векторлардың кем дегенде біреуінің қалған векторлар арқылы сызықтық өрнектелуі қажетті және жеткілікті ;дәлелдеу:қажеттілік а_1,а₂….a_n жүйесі сызықтық тәуелді болсын,яғни α₁, α₂ ,_…….α_n нақты сандары табылып α ₁a₁+ α₂a₂+… α_na_n=Ө,ал α₁ α₂…. Α_n сандардың арасында ең болмағанда біреуі нөлден өзгеше,анықтық үшін α_n ≠0 болсын.

Онда а_n=(-α ₁/ α _n ) a₁+(- α₂/ α _n)a₂+…. (-α _n-1/α _n) a_n-1

Жеткіліктілік: Анықтық үшін а_n=β₁а₁+…+ β_n-1а_n-1болсын, ондаβ₁а₁+…+ β_n-1а_n-1+

(-1) а_n= Ө. Соңғы өрнектегі а_n векторының коэффиценті нөлден өзгеше, демек а₁, а₂...а_n жүйесі сызықтық тәуелді.

4.Сызықтық тәуелсіз векторлар жүйесі. Сызықтық тәуелсіз векторлар жүйесінің қасиеттері. (дәлелдеумен)Егер α₁а₁+ α₂а₂+…. α_na_n=Ө болуы үшін α₁= α ₂= …. α_n=0 шарты қажетті болса,онда а₁,а₂,…a_n векторлар жүйесі сызықтық тәуелсіз деп аталады.қасиеттері:1)a₁≠Ө болғанда ,α*а₁=Ө тендеуінің α=0 шешімінен өзге шешімі жоқ екендігі анық,ендеше нөлден өзгеше жалғыз вектор сызықтық тәуелсіз жүйені құрайды. 2)сызықтық тәуелсіз жүйеден бірнеше векторлардан алсақ,қалған векторларда сызықтық тәуелсіз жүйені құрайды.

5.Коллинеар векторлардың анықтамасы. Екі вектордың коллинеар болу белгісі. (дәлелдеумен).Бір түзудің бойында немесе параллел түзулердің бойында орналасқан векторларды коллинеарвекторлар депатаймыз.

Анықтама: Егер екі вектордың ұзындықтары тең және бағыттары бірдей болса,онда олар тең деп аталады,яғни коллинеар векторлар.

Екі вектордың коллинеар болу белгісі:

Анық: а,b векторлары коллинеар болады егер сонда, тек сонда гана табылады жалғыз болып табылады.

а мен в коллинеар

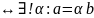
Дәлелдеу: а,b параллель түзулердің бойында жатыр.Векторды санға көбейту амалы бойынша табу. ;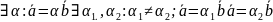

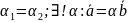векторды санға көбейту амалы бойынша оның айқын шығады.