
1
Электродина́мика — раздел физики, изучающий электромагнитное поле в наиболее общем случае (то есть, рассматриваются переменные поля, зависящие от времени) и его взаимодействие с телами, имеющими электрический заряд (электромагнитное взаимодействие)[1]. Предмет электродинамики включает связь электрических и магнитных явлений,электромагнитное излучение (в разных условиях, как свободное, так и в разнообразных случаях взаимодействии с веществом), электрический ток (вообще говоря, переменный) и его взаимодействие с электромагнитным полем (электрический ток может быть рассмотрен при этом как совокупность движущихся заряженных частиц). Любое электрическое и магнитное взаимодействие между заряженными телами рассматривается в современной физике как осуществляющееся через посредство электромагнитного поля, и, следовательно, также является предметом электродинамики.
Предмет электродинамики включает связь электрических и магнитных явлений, электромагнитное излучение (в различных условиях, как свободное, так и в различных случаях взаимодействия с веществом), электрический ток (вообще говоря, переменный) и его взаимодействие с электромагнитным полем (электрический ток может быть рассмотрен при этом как совокупность движущихся заряженных частиц). Любое электрическое и магнитное взаимодействие между заряженными телами рассматривается в современной физике как осуществляемое посредством электромагнитного поля, и, следовательно, также является предметом электродинамики.
Электри́ческий заря́д — это физическая скалярная величина, определяющая способность тел быть источником электромагнитных полей и принимать участие в электромагнитном взаимодействии.
электрический заряд дискретен, т. е. заряд любого тела составляет целое кратное отэлементарного электрического заряда е (е=1,6×10–19 Кл). Электрон (me=9,11×10–31 кг) ипротон (тp= 1,67×10–27 кг) являются соответственно носителями элементарных отрицательного и положительного зарядов.
Согласно концепции короткодействия (близкодействия), взаимодействия передаются с помощью особых материальных посредников и с конечной скоростью. Например, в случае электромагнитных взаимодействий таким посредником является электромагнитное поле.
2
Зако́н Куло́на — это закон, описывающий силы взаимодействия между точечными электрическими зарядами
Формулировка закона Кулона: «Сила электростатического взаимодействия между двумя точечными электрическими зарядами прямо пропорциональна произведению величин зарядов, обратно пропорциональна квадрату расстояния между ними и направлена вдоль соединяющей их прямой так, что одноименные заряды отталкиваются, а разноименные притягиваются».
![]() -
в векторном виде
-
в векторном виде
Напряжённость
электри́ческого по́ля — векторная физическая
величина, характеризующая электрическое
поле в данной точке и численно
равная отношению силы ![]() действующей
на неподвижный[1] пробный
заряд, помещенный в данную точку поля,
к величине этого заряда
действующей
на неподвижный[1] пробный
заряд, помещенный в данную точку поля,
к величине этого заряда ![]() :
:
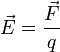 .
.
Из этого определения видно, почему напряженность электрического поля иногда называется силовой характеристикой электрического поля (действительно, всё отличие от вектора силы, действующей на заряженную частицу, только в постоянном[2] множителе).
В
каждой точке пространства в данный
момент времени существует свое значение
вектора ![]() (вообще
говоря - разное[3] в
разных точках пространства), таким
образом,
-
это векторное
поле. Формально это выражается в
записи
(вообще
говоря - разное[3] в
разных точках пространства), таким
образом,
-
это векторное
поле. Формально это выражается в
записи
![]()
При́нцип суперпози́ции — один из общих законов во многих разделах физики. В самой простой формулировке принцип суперпозиции гласит:
результат воздействия на частицу нескольких внешних сил есть векторная сумма воздействия этих сил
Наиболее известен принцип суперпозиции в электростатике, в которой он утверждает, что напряженность электростатического поля, создаваемого в данной точке системой зарядов, есть сумма напряженностей полей отдельных зарядов.
3
Зако́н Куло́на — это закон, описывающий силы взаимодействия между точечными электрическими зарядами
Формулировка закона Кулона: «Сила электростатического взаимодействия между двумя точечными электрическими зарядами прямо пропорциональна произведению величин зарядов, обратно пропорциональна квадрату расстояния между ними и направлена вдоль соединяющей их прямой так, что одноименные заряды отталкиваются, а разноименные притягиваются».
- в векторном виде
Дипо́ль — идеализированная система, служащая для приближённого описания поля, создаваемого, вообще говоря, более сложными системами зарядов, а также для приближенного описания действия внешнего поля на такие системы. Дипольное приближение, выполнение которого обычно подразумевается, когда говорится о поле диполя, основано на разложении потенциалов поля в ряд по степеням радиус-вектора, характеризующего положение зарядов-источников, и отбрасывании всех членов выше первого порядка[1]. Полученные функции будут эффективно описывать поле в случае, если:
размеры излучающей поле системы малы по сравнению с рассматриваемыми расстояниями, так что отношение характерного размера системы к длине радиус-вектора является малой величиной и имеет смысл рассмотрение лишь первых членов разложения потенциалов в ряд;
член первого порядка в разложении не равен 0, в противном случае нужно использовать приближение более высокой мультипольности;
в уравнениях рассматриваются градиенты потенциалов не выше первого порядка.
Электрический диполь — идеализированная электронейтральная система, состоящая из точечных и равных по абсолютной величине положительного и отрицательногоэлектрических зарядов.
Другими словами, электрический диполь представляет собой совокупность двух равных по абсолютной величине разноимённых точечных зарядов, находящихся на некотором расстоянии друг от друга
4
Теорема Гаусса для электрического поля в вакууме
Общая формулировка: Поток вектора напряжённости электрического поля через любую произвольно выбранную замкнутую поверхность пропорционален заключённому внутри этой поверхности электрическому заряду.
СГС |
СИ |
|
|
где
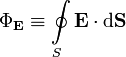 —
поток
вектора напряжённости электрического
поля через замкнутую поверхность
—
поток
вектора напряжённости электрического
поля через замкнутую поверхность 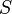 .
.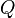 —
полный
заряд, содержащийся в объёме, который
ограничивает поверхность
.
—
полный
заряд, содержащийся в объёме, который
ограничивает поверхность
.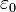 — электрическая
постоянная.
— электрическая
постоянная.
Данное выражение представляет собой теорему Гаусса в интегральной форме.
Замечание: поток вектора напряжённости через поверхность не зависит от распределения заряда (расположения зарядов) внутри поверхности.
поток вектора напряженности электрического поля через любую замкнутую поверхность равен сумме зарядов, находящихся внутри этой поверхности, деленную на электрическую постоянную εo:
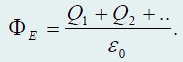
Эта важнейшая теорема впервые сформулирована немецким математиком К. Гауссом и носит его имя (теорема Гаусса). В отличие от напряженности поля, которая является точечной характеристикой поля (определена в каждой точке поля), поток этого вектора есть характеристика некоторого объема (усредненной, интегральной) характеристикой. Если в некоторой части пространства электрическое поле отсутствует (напряженность равна нулю), то и поток вектора напряженности через любую поверхность, находящуюся в этой части также равен нулю. Обратное утверждение не верно − если поток вектора напряженности равен нулю, то из этого не следует, что поле отсутствует. Единственный вывод, который можно сделать из равенства потока нулю − внутри рассматриваемой поверхности суммарный заряд равен нулю. Заряды, находящиеся вне рассматриваемой замкнутой поверхности, создают электрическое поле, в том числе и внутри объема, ограниченного рассматриваемой поверхностью. Только суммарный поток поля созданного этими зарядами равен нулю («сколько втекает − столько вытекает»). Можно сказать, что заряды вне поверхности, перераспределяют поток поля, создаваемый зарядами внутри поверхности
5
-
Однородное электростатическое поле:
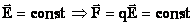 в
каждой точке поля.
в
каждой точке поля. 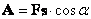 . Следовательно:
. Следовательно:



W=qEr

Т.к. если вектор перемещения перпендикулярен вектору силы (напряженности поля), работа поля равна нулю, то работа электростатического поля по перемещению заряда по любой траектории определяется разностью координат этих точек.
Если обозначить координаты заряда в начальной и последующей точках r1 и r2, то:

Т.е. работа равна разности двух эквивалентных величин, зависящих от характера взаимодействия и взаимного расположения. Но мы знаем, что работа - мера изменения энергии. Можно предположить: W=qEr - потенциальная энергия заряда в данной точке электростатического поля. Зависит от выбора начальной точки отсчета потенциальной энергии.
 -
наиболее общий способ расчета работы
в электростатическом пол
-
наиболее общий способ расчета работы
в электростатическом пол
Циркуляцией вектора напряженности называется работа, которую совершают электрические силы при перемещении единичного положительного заряда по замкнутому пути L
|
(13.18) |
Так как работа сил электростатического поля по замкнутому контуру равна нулю (работа сил потенциального поля), следовательно циркуляция напряженности электростатического поля по замкнутому контуру равна нулю.
![]()
10.
В электрических цепях применяются различные способы соединения конденсаторов. Соединение конденсаторов может производиться: последовательно, параллельно и последовательно-параллельно (последнее иногда называют смешанное соединение конденсаторов).
Если группа конденсаторов включена в цепь таким образом, что к точкам включения непосредственно присоединены пластины всех конденсаторов, то такое соединение называется параллельным соединением конденсаторов.
Если же соединение конденсаторов в батарею производится в виде цепочки и к точкам включения в цепь непосредственно присоединены пластины только первого и последнего конденсаторов, то такое соединение конденсаторов называется последовательным.
Последовательно-параллельным соединением конденсаторов называется цепь имеющая в своем составе участки, как с параллельным, так и с последовательным соединением конденсаторов.
Конденсатор — это элемент электрической цепи, состоящий из проводящих электродов (обкладок), разделенных диэлектриком и предназначенный для использования его емкости.
КЛАССИФИКАЦИЯ КОНДЕНСАТОРОВ
В зависимости от назначения конденсаторы разделяются на две большие группы: общего и специального назначения.
Группа общего назначения включает в себя широко применяемые конденсаторы, используемые практически в большинстве видов и классов аппаратуры. Традиционно к ней относят наиболее распространенные низковольтные конденсаторы, к которым не предъявляются особые требования.
Все остальные конденсаторы являются специальными. К ним относятся: высоковольтные, импульсные, помехоподавляющие, дозиметрические, пусковые и др.
По характеру изменения емкости различают конденсаторы постоянной емкости, переменной емкости и подстроечные. Из названия конденсаторов постоянной емкости вытекает, что их емкость является фиксированной и в процессе эксплуатации не регулируется.
По характеру изменения емкости: - постоянные; переменные; подстроечные.
По способу защиты: - незащищенные; защищенные; неизолированные; изолированные; уплотненные; герметизированные.
По назначению: - общего назначения; специального.
11.
Диэлектрик (изолятор) — вещество, практически не проводящее электрический ток. Концентрация свободных носителей заряда в диэлектрике не превышает 108 см−3. Основное свойство диэлектрика состоит в способности поляризоваться во внешнем электрическом поле.
Электрическое поле в диэлектрике.
Рассмотрим плоский однородный диэлектрический слой, расположенный между двумя разноименно заряженными плоскостями. Пусть напряженность электрического поля, которое создается этими плоскостями в вакууме, равна ,
где - поверхностная плотность зарядов на пластинах (эти заряды называют свободными). Под действием поля диэлектрик поляризуется, и на его гранях появляются поляризационные или связанные заряды. Эти заряды создают в диэлектрике электрическое поле , которое направлено против внешнего поля .
,
где - поверхностная плотность связанных зарядов. Результирующее поле внутри диэлектрика
.
Поверхностная плотность связанных зарядов меньше плотности свободных зарядов, и не все поле E0 компенсируется полем диэлектрика: часть линий напряженности проходит сквозь диэлектрик, другая часть обрывается на связанных зарядах. Вне диэлектрика . Следовательно, в результате поляризации поле внутри диэлектрика оказывается слабее, чем внешнее . Таким образом,
,
где - диэлектрическая проницаемость среды. Из формулы видно, что диэлектрическая проницаемость показывает, во сколько раз напряженность поля в вакууме больше напряженности поля в диэлектрике. Для вакуума , для диэлектриков .
13.
Условия на границе раздела двух диэлектриков.
Граничные условия для нормальных составляющих векторов D и E следуют из теоремы Гаусса. Выделим вблизи границы раздела замкнутую поверхность в виде цилиндра, образующая которого перпендикулярна к границе раздела, а основания находятся на равном расстоянии от границы (рис. 2.6).
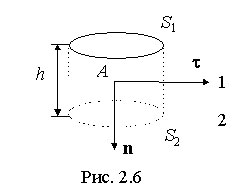
Так как на границе раздела диэлектриков нет свободных зарядов, то, в соответствии с теоремой Гаусса, поток вектора электрической индукции через данную поверхность
![]() .
.
Выделяя потоки через основания и боковую поверхность цилиндра
![]() ,
,
где ![]() -
значение
-
значение ![]() касательной
составляющей усредненное по боковой
поверхности
касательной
составляющей усредненное по боковой
поверхности ![]() .
Переходя к пределу при
.
Переходя к пределу при ![]() (при
этом
также стремится к нулю), получаем
(при
этом
также стремится к нулю), получаем ![]() ,
или окончательно для нормальных
составляющих вектора электрической
индукции
,
или окончательно для нормальных
составляющих вектора электрической
индукции
![]() .
.
Для нормальных составляющих вектора напряженности поля получим
![]() .
.
Таким
образом, при переходе через границу
раздела диэлектрических сред нормальная
составляющая вектора ![]() терпит разрыв,
а нормальная составляющая
вектора
терпит разрыв,
а нормальная составляющая
вектора ![]() непрерывна.
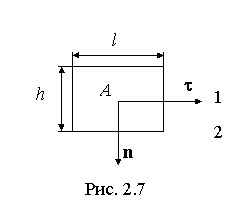
Граничные
условия для касательных составляющих
векторов D и E следуют
из соотношения, описывающего циркуляцию
вектора напряженности электрического
поля. Построим вблизи границы раздела
прямоугольный замкнутый контур длины lи
высоты h (рис.
2.7).
непрерывна.
Граничные
условия для касательных составляющих
векторов D и E следуют
из соотношения, описывающего циркуляцию
вектора напряженности электрического
поля. Построим вблизи границы раздела
прямоугольный замкнутый контур длины lи
высоты h (рис.
2.7).
Учитывая, что для электростатического поля
![]() ,
,
и обходя контур по часовой стрелке, представим циркуляцию вектора E в следующем виде:
![]() ,
,
где ![]() -
среднее значение En на
боковых сторонах прямоугольника.
Переходя к пределу при
,
получим для касательных составляющих E
-
среднее значение En на
боковых сторонах прямоугольника.
Переходя к пределу при
,
получим для касательных составляющих E
![]() .
.
Для касательных составляющих вектора электрической индукции граничное условие имеет вид
![]()
Таким
образом, при переходе через границу
раздела диэлектрических сред касательная
составляющая вектора ![]() непрерывна,
а касательная составляющая
вектора
непрерывна,
а касательная составляющая
вектора ![]() терпит разрыв.
терпит разрыв.
Электрострикция.
Электрострикция - деформация твердых, жидких и газообразных диэлектриков в электрическом поле, обусловленная их поляризацией и пропорциональная квадрату напряженности электрического поля.
В твердых телах электрострикция выражается квадратичной формулой:
![]()
где ulm - компонента тензора деформации;
Ei и Ej - составляющие напряженности электрического поля;
qijlm - коэффициенты электрострикции;
все индексы i, j, l, m принимают значения 1, 2, 3 или соответственно - х, у, z.
В газах и жидкостях электрострикцию описывают формулой:
![]() ,
,
где ![]() -
относительная объемная деформация;
-
относительная объемная деформация;
А - постоянная электрострикции.
Электрострикция обусловлена поляризацией диэлектриков в электрическом поле, т.е. смещение под действием поля атомов, несущих на себе электрические заряды (ионы, электрические диполи), или изменением ориентации диполей. Электрострикцией обладают все твердые диэлектрики независимо от их структуры и симметрии, в отличие от пьезоэффекта, который наблюдается только у сред, не имеющих центра симметрии.
Электрострикция наблюдается в жидкостях, газах, обладающих дипольными моментами. Среди жидкостей наибольшей электрострикцией также обладают дипольные, хотя, в принципе, зависимость плотности от электрического поля имеет место в любой диэлектрической жидкости. Согласно термодинамической теории, в изотропном веществе
![]() ,
,
где - сжимаемость;
- плотность;
- диэлектрическая проницаемость.
Пьезоэлектрический эффект
Пьезоэлектри́ческий эффе́кт — эффект возникновения поляризации диэлектрика под действием механических напряжений. Существует и обратный пьезоэлектрический эффект — возникновение механических деформаций под действием электрического поля. Прямой и обратный пьезоэлектрический эффекты наблюдаются в одних и тех же кристаллах — пьезоэлектриках.
Пьезоэффект нельзя путать с электрострикцией. В отличие от электрострикции, прямой пьезоэффект наблюдается только в кристаллах без центра симметрии.
Основные уравнения электростатики диэлектриков
![]()
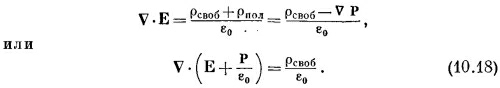
![]() -
для ротора от Е
-
для ротора от Е
![]()
14.
Энергия взаимодействия электрических зарядов
При перемещении электрических зарядов силы кулона взаимодействия между ними совершают определенную работу А. Очевидно, что мы должны приписать всякой системе зарядов определенную энергию взаимодействия, за счет убыли которой и совершается работа А:


Энергия эл.поля
Энергию заряженного конденсатора можно выразить через величины, характеризующие электрическое поле в зазоре между обкладками. Сделаем это на примере плоского конденсатора. Подстановка выражения для емкости в формулу для энергии конденсатора дает
![]()
Частное U / d равно напряженности поля в зазоре; произведение S·d представляет собой объем V, занимаемый полем. Следовательно,
![]()
Если поле однородно (что имеет место в плоском конденсаторе при расстоянии dмного меньшем, чем линейные размеры обкладок), то заключенная в нем энергия распределяется в пространстве с постоянной плотностью w. Тогда объемная плотность энергии электрического поля равна
![]()
Объемная плотность энергии эл. поля.
Это физическая
величина, численно равная отношению
потенциальной энергии поля, заключенной
в элементе объема, к этому объему. Для
однородного поля объемная плотность
энергии равна ![]() .
Для плоского конденсатора, объем которого
Sd, где S - площадь пластин, d - расстояние
между пластинами, имеем
.
Для плоского конденсатора, объем которого
Sd, где S - площадь пластин, d - расстояние
между пластинами, имеем
![]()
Выводим:
![]()
15.
Электрический ток в вакууме
Вакуум (от лат. vacuum – пустота) – состояние газа при давлении, меньшем атмосферного
Для получения электрического тока в вакууме необходимо создать в эвакуированном объеме направленный поток заряженных частиц. Для этого катод вакуумного устройства подвергают одному из видов воздействия, перечисленных в таблице 3, вследствие чего возникает эмиссия (испускание) свободных электронов. При приложении электрического поля между катодом и анодом электроны устремляются к положительно заряженному аноду – возникает электрический ток.
Таблица 3. Основные виды эмиссии электронов.
Вид эмиссии |
Условия возникновения |
Ионно-электронная |
Бомбардировка катода положительными ионами. |
Вторичная электронная |
Бомбардировка анода электронами. |
Термоэлектронная |
Нагрев катода. |
Фотоэлектронная |
Воздействие на катод электромагнитным излучением. |
термоэлектронная эмиссия - это испускание электронов нагретыми телами (обычно металлами) в вакуум или другую среду.
Выйти из тела могут только те электроны, энергия к-рых больше энергии покоящегося вне эмиттера электрона
ток с единицы поверхности нагретого металла, находящейся при однородной абсолютной температуре Т, определяется формулой
![]()
где А – постоянный множитель, k – постоянная Больцмана, а W – работа выхода, характерная для данного металла, но зависящая от состояния его поверхности
Вторичная и автоэлектронная эмиссия
Излучение электронов при бомбардировке вещества электронами или ионами называется вторичной эмиссией, а излученные электроны – вторичными электронами. Частицы, ударяющихся о поверхность и вызывающие эмиссию, называются первичными электронами и первичными ионами. Вторичную эмиссию можно вызвать бомбардировкой некоторого материала (проводника или диэлектрика) потоком первичных электронов или других частиц, обладающих высокой энергией. Эмитируемые вторичные электроны будут притягиваться к любому близлежащему электроду с более высоким положительным потенциалом, чем вторично-эмиссионный катод, и образуют поток зарядов, идущий от облучаемой поверхности, в то время как поток первичных частиц несет заряды в направлении к данной поверхности.
16.
Электрический ток в газе
1. Газы в обычных условиях—диэлектрики. Воздух используют в технике как изолятор: а) в линиях электропередач; б) между обкладками воздушных конденсаторов; в) в контактах выключателей. |
|
|
2. При определенных условиях газы — проводники: молния, электрическая искра, дуга при сварке. Процесс протекания тока через газ называетсягазовым разрядом. Свободные заряды (ионы обоих знаков и электроны) возникают в газах только в процессе ионизации. |
|
|
Ионизация газов Ионизацию вызывают: 1. Высокая температура. 2. Ультрафиолетовые лучи. 3. Рентгеновские лучи, - лучи и т. п. Ионизация осуществляется при условии: еЕ W ионизации, где — длина свободного пробега заряженных частиц. |
|
|
Нагревание – не единственный способ превращения газа в проводник. Вместо пламени можно использовать ультрафиолетовое или рентгеновское излучение, а также поток альфа-частиц или электронов. Опытами установлено, что действие любой из этих причин приводит к ионизации молекул газа. При этом от некоторых молекул отрывается один (или несколько) электронов, в результате чего молекула превращается в положительный ион. Под воздействием электрического поля, существующего между дисками, образовавшиеся ионы и электроны начинают двигаться, создавая между дисками электрический ток.
Процессы ионизации и рекомбинации.
Процесс ионизации заключается в том, что под действием высокой температуры или некоторых лучей молекулы газа теряют электроны, и тем самым превращаются в положительные ионы.
Таким образом, в результате происходит освобождение электронов из атомов и молекул, которые могут присоединиться к нейтральным молекулам или атомам, превращая их в отрицательные ионы. Ионы и свободные электроны делают газ проводником электричества.
Ионизация газа может происходить под действием коротковолнового излучения – ультрафиолетовых, рентгеновских и гамма-лучей, а также альфа-, бета- и космических лучей.
Рекомбинация – это нейтрализация при встрече разноименных ионов или воссоединение иона и электрона в нейтральную молекулу (атом).
Факторы, под действием которых возникает ионизация в газе, называют внешними ионизаторами, а возникающая при этом проводимость называется несамостоятельной проводимостью.
При данной мощности внешнего ионизатора в объёме газа устанавливается равновесное состояние, при котором число пар ионов, возникающих под действием ионизатора за одну секунду в единице объёма, равно числу пар рекомбинировавших ионов. При этом скорость ионизации равна скорости рекомбинации:
|
|
Понятие о плазме
Плазмой называется ионизованный квазинейтральный газ, занимающий настолько большой объем, что в нем не происходит сколько-нибудь заметного нарушения квазинейтральности из-за тепловых флуктуаций.
Плазма, возникающая в газовом разряде, носит название газоразрядной; к ней относятся положительный столб тлеющего разряда, канал искрового и дугового разрядов.
Положительный столб представляет собой так называемую неизотермическую плазму. В такой плазме средние кинетические энергии электронов, ионов и нейтральных молекул (атомов) различны.
Важнейшие свойства плазмы:
сильное взаимодействие с внешними магнитными и электрическими полями, связанное с ее высокой электропроводностью;
специфическое коллективное взаимодействие частиц плазмы, осуществляющееся через усредненные электрические и магнитные поля, которые создают сами эти частицы;
благодаря коллективным взаимодействиям плазма ведет себя как своеобразная упругая среда, в которой легко возбуждаются и распространяются различного рода колебания и волны (например, ленгмюровские колебания плазмы);
во внешнем магнитном поле плазма ведет себя как диамагнитная среда;
удельная электрическая проводимость σ полностью ионизованной плазмы не зависит от плотности плазмы и увеличивается с ростом термодинамической температуры, пропорционально
 .
При Т ≥
107 К,
σ столь велика, что плазму можно
приближенно считать идеальным проводником
(
.
При Т ≥
107 К,
σ столь велика, что плазму можно
приближенно считать идеальным проводником
( ).
).
Плазма – наиболее распространенное состояние вещества во Вселенной. Солнце и другие звезды состоят из полностью ионизованной высокотемпературной плазмы
Электропроводность плазмы
Электропроводность плазмы может быть очень большой и по характеру приближается к электронной электропроводности металлов. Плазма имеется в положительном столбе тлеющего разряда и в главном канале искрового разряда.
Электропроводность плазмы ( а) определяется ее температурой [10], которая, в свою очередь, зависит от удельной мощности Р, выделяющейся в плазме
17.
Электролиты
Электролиты - жидкие или твёрдые вещества и системы, в которых присутствуют в сколько-нибудь заметной концентрации ионы, обусловливающие прохождение электрического тока. В узком смысле Электролиты называются вещества, растворы которых проводят электрический ток ионами, образующимися в результате электролитической диссоциации
Электролиз
Электролиз-Этот окислительно-восстановительный процесс протекает на электродах при прохождении постоянного электрического тока через растворы или расплавыэлектролитов. На отрицательно заряженном электроде - катоде происходит электрохимическое восстановление частиц (атомов, молекул, катионов), а на положительно заряженном электроде - аноде идет электрохимическое окисление частиц (атомов, молекул, анионов).
Законы электролиза
Количественные характеристики электролиза * выражаются двумя законами Фарадея:
1) Масса вещества, выделяющегося на электроде *, прямо пропорциональна количеству электричества, прошедшего через электролит *.
2) При электролизе различных химических соединений одинаковые количества электричества выделяют на электродах массы веществ, пропорциональные их электрохимическим эквивалентам.
Эти два закона можно объединить в одном уравнении:
![]() ,
,
где m – масса выделяющегося вещества, г;
n – количество электронов, переносимых в электродном процессе;
F – число Фарадея (F=96485 Кл/моль)
I – сила тока, А;
t – время, с;
M – молярная масса выделяющегося вещества, г/моль.
Величина ![]() называется
электрохимическим эквивалентом вещества.
Если продолжительность электролиза
измерять в часах, то число Фарадеядолжно
быть выражено в ампер-часах. В этом
случае F=26,8 А·ч/моль.
называется
электрохимическим эквивалентом вещества.
Если продолжительность электролиза
измерять в часах, то число Фарадеядолжно
быть выражено в ампер-часах. В этом
случае F=26,8 А·ч/моль.
Вследствие
параллельных побочных процессов масса
вещества, получаемого при электролизе,
оказывается часто меньше той, которая
соответствует количеству прошедшего
электричества. Отношение массы вещества,
реально выделенного на электроде, к теоретической
и умноженное на 100%, называют выходом по
току: ![]() .
.
Электрохимические потенциалы
Электрохимический потенциал
термодинамическая
функция, характеризующая состояние
какого-либо компонента, состоящего из
заряженных частиц (электронов, ионов),
в фазе данного состава. Э. п. может быть
определён как приращение любого из
потенциалов термодинамических
(См. Потенциалы
термодинамические)
системы при введении в неё одной
заряженной частицы i-того
компонента при неизменных всех остальных
переменных, от которых зависит
рассматриваемый потенциал. Э. п. ![]()
![]()
где μ — Химический потенциал i-того компонента, zi, — заряд частицы, φ — электрический потенциал, е — элементарный заряд; член zieφ выражает работу по преодолению электрических сил. Если Э. п. относится к 1 молю вещества, этот член равен ziFφ, где F — Фарадея число.
Закон Ома для электролитов
Общая плотность тока в электролитах будет складываться из плотности тока, создаваемой «+» и «-» ионами
 (19)
(19)
Плотность тока определяется через скорость движения
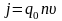 ,
(20)
,
(20)
где q0 – заряд переносимый одним ионом, n – число ионов
n = α·n0, (21)
где n0 – концентрация.
 (22)
(22)
Скорость
ионов, отнесенная к напряженности
электрического поля называется
подвижностью ионов (U).
Выразим
 из уравнения (22)
из уравнения (22)
 (23)
(23)
Правые части уравнений (21) и (23) подставим в уравнение (20), получим
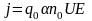 ,
(24)
,
(24)
с учетом уравнения (24) уравнение (19) перепишется

 (25)
– закон Ома для электролитов.
(25)
– закон Ома для электролитов.
Если
выражение
 - удельная электропроводность, то
уравнение (25) перепишется
- удельная электропроводность, то
уравнение (25) перепишется
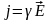
Проводимость электролитов зависит пропорционально температуре, так как при повышении температуры возрастает подвижность ионов.
18.
Электропроводность металлов.
Электропроводность- электрическая проводимость, проводимость, способность тела пропускать Электрический ток под воздействием электрического поля, а также физическая величина, количественно характеризующая эту способность
Уровни Ферми
Энергия
Ферми - максимальная энергия электронов
при температуре в 0 К. Энергия Фермирастет
с увеличением количества электронов в
квантовой системе и, соответственно,
уменьшается с уменьшением количества
электронов (фермионов).
Это обусловливается возникающим
интенсивным обменным и электростатическим
взаимодействием в области перекрытия
зарядовых плотностей волновых функций
электронов при росте количества
электронов.
Энергия
и импульс Ферми есть граничными энергией
и импульсом перехода электрона в
свободное состояние. Поверхность в
пространстве импульсов при 0 К, под
которой все квантовые состояния заняты
(то есть, нахождение электронов на
заполненных орбиталях),
есть поверхностью Ферми.
При
увеличении температуры возникает
корреляция атомов и выделяются фононы,
которые поглощаются электронами. В
результате импульс электронов превышает
граничный импульс Ферми, и они переходят
в разрешенную зону (формально, есть
квазисвободными частицами).
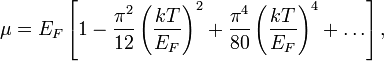
Явление сверхпроводимости
Некоторые вещества при сильном охлаждении перестают оказывать сопротивление электрическому току. Такие вещества называются сверхпроводниками. Сверхпроводники применяют в медицине, транспорте, ядерной физике и других сферах.
19.
Полупроводник — это вещество, основным электрическим свойством которого является сильная зависимость его электропроводности от воздействия внешних факторов (температуры, электрического поля, света и т. д.).
Собственная проводимость
Полупроводники, в которых свободные электроны и «дырки» появляются в процессе ионизации атомов, из которых построен весь кристалл, называют полупроводниками с собственной проводимостью. В полупроводниках с собственной проводимостью концентрация свободных электронов равняется концентрации «дырок».
Проводимость связана с подвижностью частиц следующим соотношением:
![]() где
где ![]() —
удельное сопротивление,
—
удельное сопротивление, ![]() — подвижность
электронов,
— подвижность
электронов, ![]() —
подвижность дырок,
—
подвижность дырок, ![]() —
их концентрация, q — элементарный
электрический заряд (1,602·10−19 Кл).
—
их концентрация, q — элементарный
электрический заряд (1,602·10−19 Кл).
Для собственного полупроводника концентрации носителей совпадают и формула принимает вид:
![]()
Примесная проводимость
Для создания полупроводниковых приборов часто используют кристаллы с примесной проводимостью. Такие кристаллы изготавливаются с помощью внесения примесей с атомами трехвалентного или пятивалентного химического элемента.
Электронные полупроводники
Этот вид полупроводников имеет примесную природу. В четырёхвалентный полупроводник (например, кремний) добавляют примесь пятивалентного полупроводника (например,мышьяка). В процессе взаимодействия каждый атом примеси вступает в ковалентную связь с атомами кремния. Однако для пятого электрона атома мышьяка нет места в насыщенных валентных связях, и он переходит на дальнюю электронную оболочку. Там для отрыва электрона от атома нужно меньшее количество энергии. Электрон отрывается и превращается в свободный. В данном случае перенос заряда осуществляется электроном, а не дыркой, то есть данный вид полупроводников проводит электрический ток подобно металлам. Примеси, которые добавляют в полупроводники, вследствие чего они превращаются в полупроводники n-типа, называются донорными.
Проводимость N-полупроводников приблизительно равна:
![]()
Дырочные полупроводники
Этот вид полупроводников, кроме примесной основы, характеризуется дырочной природой проводимости. В четырёхвалентный полупроводник (например, в кремний) добавляют небольшое количество атомов трехвалентного элемента (например, индия). Каждый атом примеси устанавливает ковалентную связь с тремя соседними атомами кремния. Для установки связи с четвёртым атомом кремния у атома индия нет валентного электрона, поэтому он захватывает валентный электрон из ковалентной связи между соседними атомами кремния и становится отрицательно заряженным ионом, вследствие чего образуется дырка.
ВОЛНОВЫЕ ЯВЛЕНИЯ НА ГРАНИЦЕ РАЗДЕЛА ДВУХ СРЕД ПОЛЕ ОДНОРОДНОЙ ПЛОСКОЙ ВОЛНЫ, РАСПРОСТРАНЯЮЩЕЙСЯ В ПРОИЗВОЛЬНОМ НАПРАВЛЕНИИ
Попадая на поверхность раздела двух сред, электромагнитная волна может частично (или полностью) отразиться либо частично (либо полностью) пройти в другую среду. Кроме того, возможно и более сложное явление, называемое дифракцией волн
20.
Магни́тное по́ле — силовое поле, действующее на движущиеся электрические заряды и на тела, обладающие магнитным моментом, независимо от состояния их движения, магнитная составляющая электромагнитного поля
Магнитное поле может создаваться током заряженных частиц и/или магнитными моментами электронов в атомах (и магнитными моментами другихчастиц, хотя в заметно меньшей степени) (постоянные магниты).
Кроме этого, оно появляется при наличии изменяющегося во времени электрического поля.
Основной силовой
характеристикой магнитного поля
является вектор
магнитной индукции ![]() (вектор
индукции магнитного поля)[3][4].
С математической точки зрения
(вектор
индукции магнитного поля)[3][4].
С математической точки зрения ![]() — векторное
поле, определяющее и конкретизирующее
физическое понятие магнитного поля.
Нередко вектор магнитной индукции
называется для краткости просто магнитным
полем (хотя, наверное, это не самое
строгое употребление термина).
— векторное
поле, определяющее и конкретизирующее
физическое понятие магнитного поля.
Нередко вектор магнитной индукции
называется для краткости просто магнитным
полем (хотя, наверное, это не самое
строгое употребление термина).
Ещё одной фундаментальной характеристикой магнитного поля (альтернативной магнитной индукции и тесно с ней взаимосвязанной, практически равной ей по физическому значению) является векторный потенциал.
Электромагнитная индукция
Если поток вектора магнитной индукции через замкнутый контур меняется во времени, в этом контуре возникает ЭДС электромагнитной индукции, порождаемая (в случае неподвижного контура) вихревым электрическим полем, возникающим вследствие изменения магнитного поля со временем (в случае неизменного со временем магнитного поля и изменения потока из-за движения контура-проводника такая ЭДС возникает посредством действия силы Лоренца)
Взаимодействие электромагнитного поля и движущегося заряда.
На электрический заряд, движущийся в магнитном поле, действует сила Лоренца, равная
![]() (59)
(59)
где q - величина заряда, Кл; u — скорость заряда, м/с; В —магнитная индукция поля, Г. Эта сила направлена перпендикулярно векторам u и В.
Если проводящий контур движется а стационарном магнитном поле, то в нем наводится э.д.с. индукции, поскольку на каждый свободный заряд — носитель тока в проводнике, перемещающийся вместе с проводником в магнитном поле, действует сила Лоренца, поэтому на отрезке длиной l, движущемся в поле с магнитной индукцией В со скоростью u возникает э.л.с., равная
E=-B l u, B
21.
Закон Био́—Савара—Лапла́са — физический закон для определения вектора индукции магнитного поля, порождаемого постоянным электрическим током.
Пусть
постоянный ток ![]() течёт
по контуру (проводнику)
течёт
по контуру (проводнику) ![]() ,
находящемуся в вакууме,
,
находящемуся в вакууме, ![]() —
точка, в которой ищется (наблюдается)
поле, тогда индукция магнитного
поля в этой точке выражается интегралом
(в Международной
системе единиц (СИ))
—
точка, в которой ищется (наблюдается)
поле, тогда индукция магнитного
поля в этой точке выражается интегралом
(в Международной
системе единиц (СИ))
![]()
где
квадратными скобками обозначено векторное
произведение, ![]() —
положение точек контура
,
—
положение точек контура
, ![]() —
вектор элемента контура (ток течет вдоль
него);
—
вектор элемента контура (ток течет вдоль
него); ![]() — магнитная
постоянная;
— магнитная
постоянная; ![]() —
единичный вектор, направленный от
элемента контура к точке наблюдения.
Если
взять за точку отсчёта точку, в которой
нужно найти вектор магнитной индукции,
то формула упрощается:
—
единичный вектор, направленный от
элемента контура к точке наблюдения.
Если
взять за точку отсчёта точку, в которой
нужно найти вектор магнитной индукции,
то формула упрощается:
где ![]() —
вектор, описывающий кривую проводника
с током
,
—
модуль
,
—
вектор магнитной индукции, создаваемый
элементом проводника
—
вектор, описывающий кривую проводника
с током
,
—
модуль
,
—
вектор магнитной индукции, создаваемый
элементом проводника ![]() .
.
Направление ![]() перпендикулярно
плоскости, в которой лежат векторы
перпендикулярно
плоскости, в которой лежат векторы ![]() и
и ![]() .
Направление вектора магнитной индукции
может быть найдено по правилу
правого винта: направление вращения
головки винта дает направление
,
если поступательное движение буравчика
соответствует направлению тока в
элементе. Модуль вектора
определяется
выражением (в системе СИ)
.
Направление вектора магнитной индукции
может быть найдено по правилу
правого винта: направление вращения
головки винта дает направление
,
если поступательное движение буравчика
соответствует направлению тока в
элементе. Модуль вектора
определяется
выражением (в системе СИ)
22.
Если магнитное поле создается несколькими проводниками с током, то индукция результирующего поля есть векторная сумма индукций полей, создаваемых каждым проводником в отдельности.
Индукцию ![]() проводника
с током можно представить как векторную
сумму элементарных индукций
проводника
с током можно представить как векторную
сумму элементарных индукций ![]() создаваемых
отдельными участками проводника. На
опыте невозможно выделить отдельный
участок проводника с током, так как
постоянные токи всегда замкнуты. Можно
измерить только суммарную индукцию
магнитного поля, создаваемого всеми
элементами тока. Закон
Био–Савара определяет
вклад
создаваемых
отдельными участками проводника. На
опыте невозможно выделить отдельный
участок проводника с током, так как
постоянные токи всегда замкнуты. Можно
измерить только суммарную индукцию
магнитного поля, создаваемого всеми
элементами тока. Закон
Био–Савара определяет
вклад ![]() в
магнитную индукцию
результирующего
магнитного поля, создаваемый малым
участком Δlпроводника
с током I.
в
магнитную индукцию
результирующего
магнитного поля, создаваемый малым
участком Δlпроводника
с током I.
|
Здесь r – расстояние от данного участка Δl до точки наблюдения, α – угол между направлением на точку наблюдения и направлением тока на данном участке, μ0 – магнитная постоянная. Направление вектора определяется правилом буравчика: оно совпадает с направлением вращения рукоятки буравчика при его поступательном перемещении вдоль тока
Расчеты магнитного поля часто упрощаются при учете симметрии в конфигурации токов, создающих поле. В этом случае можно пользаоваться теоремой о циркуляции вектора магнитной индукции, которая в теории магнитного поля токов играет ту же роль, что и теорема Гаусса в электростатике.
Теорема о циркуляции утверждает, что циркуляция вектора магнитного поля постоянных токов по любому контуру L всегда равна произведению магнитной постоянной μ0на сумму всех токов, пронизывающих контур:
|
еорема о циркуляции в данном примере выражается соотношением:
|
Теорема о циркуляции в общем виде следует из закона Био–Савара и принципа суперпозиции.
